Inada-Bedingungen

Als Inada-Bedingungen bezeichnet man in der neoklassischen Produktions- und Wachstumstheorie mehrere Bedingungen, die üblicherweise an die verwendeten Produktionsfunktionen gestellt werden. Die Bezeichnung geht auf einen Artikel des japanischen Ökonomen Ken-Ichi Inada aus dem Jahr 1963 zurück, in dem er diese explizit für ein Wachstumsmodell formuliert.[1]

Die Bezeichnung „Inada-Bedingungen“ wird dabei in der Literatur unscharf verwendet; der überwiegende Teil der Autoren beschränkt sich auf die untenstehenden Anforderungen, andere rechnen den Inada-Bedingungen darüber hinaus auch andere klassischerweise vorausgesetzte (und eben auch von Inada übernommene) Bedingungen zu, wie beispielsweise die Annahme abnehmender Grenzproduktivität (siehe auch der nachfolgende Abschnitt).[2]

Erläuterung

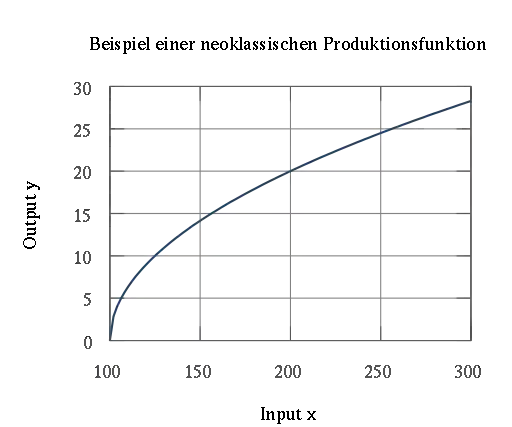
Beispiel einer Produktionsfunktion, die die Inada-Bedingungen erfüllt

Sei $F(K,L)$ eine Produktionsfunktion, wobei $K$ für den Kapitaleinsatz und $L$ für den Arbeitseinsatz steht. Dann besagen die Inada-Bedingungen (im engeren Sinne), dass das Grenzprodukt eines jeden Produktionsfaktors gegen unendlich konvergiert, wenn man nur den jeweiligen Faktoreinsatz gegen null streben lässt; lässt man den jeweiligen Faktoreinsatz hingegen gegen unendlich streben, so konvergiert das Grenzprodukt des Faktors gegen null. Formell gilt also

\lim _{K\to 0}{\frac {\partial F(K,L)}{\partial K}}=\infty \quad {\textrm {und}}\quad \lim _{K\to \infty }{\frac {\partial F(K,L)}{\partial K}}=0

beziehungsweise

\lim _{L\to 0}{\frac {\partial F(K,L)}{\partial L}}=\infty \quad {\textrm {und}}\quad \lim _{L\to \infty }{\frac {\partial F(K,L)}{\partial L}}=0

.

Eine typische, für technische Zwecke hilfreiche Lesart dieser Bedingungen ist zum Beispiel, dass bei gegebener Technologie in einer Volkswirtschaft der Output nicht beliebig gesteigert werden kann, indem der Arbeitseinsatz immer weiter erhöht wird.[3]

Im weiteren Sinne bezeichnen die Inada-Bedingungen die folgenden 6 Eigenschaften in Anlehnung an die Formulierung von Hirofumi Uzawa:[4] für eine Funktion $f(x)$ gilt

der Wert der Funktion $f(x)$ an der Stelle 0 ist 0: $f(0)=0$
die Funktion ist zweimal stetig differenzierbar,
die Funktion ist streng monoton steigend in $x_{i}$ : $\partial f(x)/\partial x_{i}>0$ ,
die zweite Ableitung der Funktion ist negativ in $x_{i}$ (demnach handelt es sich um eine konkave Funktion): $\partial ^{2}f(x)/\partial x_{i}^{2}<0$ ,
der Grenzwert der ersten Ableitung ist positiv unendlich für $x_{i}$ gegen 0: $\lim _{x_{i}\to 0}\partial f(x)/\partial x_{i}=+\infty$ ,
und der Grenzwert der ersten Ableitung ist null für $x_{i}$ gegen unendlich: $\lim _{x_{i}\to +\infty }\partial f(x)/\partial x_{i}=0$ .

Implikationen

Unterstellt man, wie dies typischerweise für Produktionsfunktionen angenommen wird, dass beide Inputfaktoren eine positive aber abnehmende Grenzproduktivität aufweisen, dass also gilt:

{\frac {\partial F(K,L)}{\partial K}}>0\quad {\textrm {sowie}}\quad {\frac {\partial ^{2}F(K,L)}{\partial K^{2}}}<0

beziehungsweise

{\frac {\partial F(K,L)}{\partial L}}>0\quad {\textrm {sowie}}\quad {\frac {\partial ^{2}F(K,L)}{\partial L^{2}}}<0

,

und dass die Produktionsfunktion über konstante Skalenerträge verfügt (= homogen vom Grade eins ist):

F(\alpha K,\alpha L)=\alpha F(K,L)\quad (\alpha \in \mathbb {R} ^{+})

,

dann folgt aus den obigen Inada-Bedingungen überdies[5], dass jeder eingesetzte Faktor essenziell (auch: wesentlich) ist. Damit ist gemeint, dass eine Volkswirtschaft in einem Zustand, in dem es entweder kein Kapital oder keine Arbeit gibt, keinerlei Output generieren kann. Formell:

F(K,0)=0\quad {\textrm {und}}\quad F(0,L)=0

.

Genügt eine Produktionsfunktion den Inada-Bedingungen, sind daher Randlösungen ausgeschlossen, bei denen ein Faktoreinsatz im Gewinnmaximum verschwindet oder unbeschränkt wächst.

Es wurde vermutet, dass die Inada-Bedingungen implizieren, dass die Produktionsfunktion asymptotisch vom Cobb-Douglas-Typ sein muss, da sie davon ausgingen, dass alle Funktionen die asymptotisch eine Substitutionselastizität von eins aufweisen zur Klasse der Cobb-Douglas-Funktionen gehören.[6] Es zeigte sich allerdings jedoch, dass die Inada-Bedingungen implizieren, dass für diese Eigenschaft die Produktionsfunktion nicht notwendigerweise vom Cobb-Douglas-Typ sein muss.[7]

Literatur

Rolf Färe und Daniel Primont: Inada Conditions and the Law of Diminishing Returns. In: International Journal of Business and Economics. 1, Nr. 1, 2002, S. 1–8 (kostenfrei online; PDF; 166 kB).
Ken-Ichi Inada: On a Two-Sector Model of Economic Growth: Comments and a Generalization. In: The Review of Economic Studies. 30, Nr. 2, 1963, S. 119–127 (JSTOR 2295809).

Anmerkungen

Inada 1963.
Wie hier zum Beispiel Färe/Primont 2002; Stefan Baumgärtner: The Inada Conditions for Material Resource Inputs Reconsidered. In: Environmental & Resource Economics. 29, Nr. 3, 2004, S. 307–322, doi:10.1007/s10604-003-5267-5; Knut Sydsæter u. a.: Further Mathematics for Economic Analysis. 2. Auflage. Pearson 2008, S. 214; weiter gefasst hingegen beispielsweise Thomas Wagner und Elke J. Jahn: Neue Arbeitsmarkttheorien. 2. Auflage. Lucius & Lucius (UTB), Stuttgart 2004, ISBN 3828202535.
Ein praktisches Beispiel für den Einsatz der Bedingung liefern Wagner/Jahn 2004: Für den Unternehmensgewinn gelte $\pi (L,w)=F(K,L)-wL$ ( $w$ : Reallohn). Hätte nun bei gegebenem Kapitalbestand $K={\overline {K}}$ jeder Arbeitnehmer in der Volkswirtschaft eine Grenzproduktivität, die oberhalb des sich auf dem Markt bildenden Reallohns liegt, wäre also für jeden Arbeiter $i$
${\frac {\partial F({\overline {K}},L_{i})}{\partial L_{i}}}>w\quad (\forall i)$ ,
dann würde generell für die partielle Ableitung der Gewinnfunktion nach $L$ , also
${\frac {\partial \pi (L,w)}{\partial L}}={\frac {\partial F({\overline {K}},L)}{\partial L}}-w$
gelten, dass diese stets positiv ist. Damit könnte das Unternehmen aber ohne die Inada-Bedingungen theoretisch einen unendlich hohen Gewinn erwirtschaften, indem es einen immer größeren Arbeitseinsatz nachfragt. Vgl. Thomas Wagner und Elke J. Jahn: Neue Arbeitsmarkttheorien. 2. Auflage. Lucius & Lucius (UTB), Stuttgart 2004, ISBN 3828202535, S. 29.
Uzawa, Hirofumi. "On a two-sector model of economic growth II." The Review of Economic Studies (1963): 105–118. S. 108.
Ein Beweis findet sich zum Beispiel bei Färe/Primont 2002, S. 3 f.
Vgl. Paulo Barelli und Samuel de Abreu Pessôa: Inada conditions imply that production function must be asymptotically Cobb–Douglas. In: Economics Letters. 81, Nr. 3, 2003, S. 361–363, doi:10.1016/S0165-1765(03)00218-0.
Litina, Anastasia, and Theodore Palivos. "Do Inada conditions imply that production function must be asymptotically Cobb–Douglas? A comment." Economics Letters 99.3 (2008): 498–499.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Inada 1963.

[2] Wie hier zum Beispiel Färe/Primont 2002; Stefan Baumgärtner: The Inada Conditions for Material Resource Inputs Reconsidered. In: Environmental & Resource Economics. 29, Nr. 3, 2004, S. 307–322, doi:10.1007/s10604-003-5267-5; Knut Sydsæter u. a.: Further Mathematics for Economic Analysis. 2. Auflage. Pearson 2008, S. 214; weiter gefasst hingegen beispielsweise Thomas Wagner und Elke J. Jahn: Neue Arbeitsmarkttheorien. 2. Auflage. Lucius & Lucius (UTB), Stuttgart 2004, ISBN 3828202535.

[3] Ein praktisches Beispiel für den Einsatz der Bedingung liefern Wagner/Jahn 2004: Für den Unternehmensgewinn gelte $\pi (L,w)=F(K,L)-wL$ ( $w$ : Reallohn). Hätte nun bei gegebenem Kapitalbestand $K={\overline {K}}$ jeder Arbeitnehmer in der Volkswirtschaft eine Grenzproduktivität, die oberhalb des sich auf dem Markt bildenden Reallohns liegt, wäre also für jeden Arbeiter $i$
${\frac {\partial F({\overline {K}},L_{i})}{\partial L_{i}}}>w\quad (\forall i)$ ,
dann würde generell für die partielle Ableitung der Gewinnfunktion nach $L$ , also
${\frac {\partial \pi (L,w)}{\partial L}}={\frac {\partial F({\overline {K}},L)}{\partial L}}-w$
gelten, dass diese stets positiv ist. Damit könnte das Unternehmen aber ohne die Inada-Bedingungen theoretisch einen unendlich hohen Gewinn erwirtschaften, indem es einen immer größeren Arbeitseinsatz nachfragt. Vgl. Thomas Wagner und Elke J. Jahn: Neue Arbeitsmarkttheorien. 2. Auflage. Lucius & Lucius (UTB), Stuttgart 2004, ISBN 3828202535, S. 29.

[4] Uzawa, Hirofumi. "On a two-sector model of economic growth II." The Review of Economic Studies (1963): 105–118. S. 108.

[5] Ein Beweis findet sich zum Beispiel bei Färe/Primont 2002, S. 3 f.

[6] Vgl. Paulo Barelli und Samuel de Abreu Pessôa: Inada conditions imply that production function must be asymptotically Cobb–Douglas. In: Economics Letters. 81, Nr. 3, 2003, S. 361–363, doi:10.1016/S0165-1765(03)00218-0.

[7] Litina, Anastasia, and Theodore Palivos. "Do Inada conditions imply that production function must be asymptotically Cobb–Douglas? A comment." Economics Letters 99.3 (2008): 498–499.