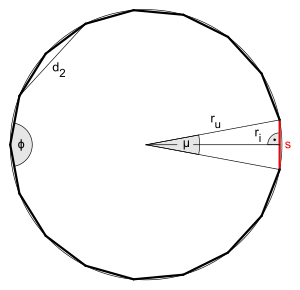
Siebzehneck
Das Siebzehneck oder Heptadekagon ist eine geometrische Figur, die zur Gruppe der Vielecke (Polygone) gehört. Es ist definiert durch siebzehn Punkte, die durch siebzehn Strecken zu einem geschlossenen Linienzug verbunden sind.

Dieser Artikel behandelt im Folgenden das regelmäßige Siebzehneck, das konvex ist, siebzehn gleich lange Seiten hat und dessen Ecken auf einem gemeinsamen Umkreis liegen, sowie das regelmäßige überschlagene Siebzehneck.
Eigenschaften
Das Besondere an einem regelmäßigen Siebzehneck ist die Tatsache, dass es konstruierbar ist – es kann somit unter alleiniger Verwendung von Zirkel und Lineal (den euklidischen Werkzeugen) gezeichnet werden –, diese Konstruierbarkeit jedoch über Jahrtausende nicht nachgewiesen werden konnte. Der Nachweis gelang erst Carl Friedrich Gauß im Jahr 1796.[1] Er zeigte, dass für den Kosinus des Zentriwinkels
gilt, woraus sich die Konstruierbarkeit ergibt. Außerdem lassen sich damit auch verschiedene Größen des Siebzehnecks wie Seitenlänge, Umfang, Inkreisradius, Diagonale über zwei Seiten und Flächeninhalt berechnen.
Am 21. Juni 1801 stellte Gauß der St. Petersburger Akademie für seine obige Formel eine sogenannte Kurzfassung in drei Schritten vor, die sich aus der Gruppierung von Summen einzelner Kosinuswerte ergibt. Friedrich L. Bauer beschreibt sie, im Jahr 2009, in seinem Buch Historische Notizen zur Informatik im Kapitel Carl Friedrich Gauß, das 17-Eck und MATHEMATICA[2] ausführlich, es sei deshalb hier nur das Ergebnis der Kurzfassung erwähnt.
Mit den darin u. a. eingeführten Hilfsgrößen und
- und
gilt somit für den Kosinus des Zentriwinkels auch
- sowie
- [3]
| Seitenlänge |
| ||
| Umfang | |||
| Inkreisradius | |||
| Diagonale über zwei Seiten | |||
| Flächeninhalt | |||
| Innenwinkel |
Mathematischer Hintergrund

Der Entdeckung von Gauß liegt eine Auflösung der Kreisteilungsgleichung zugrunde, deren Lösungen – es handelt sich um die siebzehnten Einheitswurzeln – in der Gaußschen Zahlenebene der komplexen Zahlen ein regelmäßiges Siebzehneck mit Radius 1 bilden. Diese Gleichung kann allein durch den Gebrauch geschachtelter Quadratwurzeln gelöst werden (siehe oben für den Realteil der Lösung , die entgegen dem Uhrzeigersinn zur Lösung 1 am nächsten liegt). Gauß erkannte 1796 als 18-Jähriger diese Möglichkeit „Durch angestrengtes Nachdenken … am Morgen … (ehe ich aus dem Bette aufgestanden war)“[4] aufgrund allgemeiner zahlentheoretischer Eigenschaften von Primzahlen, in diesem Fall konkret der Primzahl 17: Die modulo einer Primzahl gebildeten, von 0 verschiedenen Restklassen können nämlich als Potenzen einer sogenannten Primitivwurzel dargestellt werden, wobei im Fall konkret gewählt werden kann:
Sortiert man nun die von 1 verschiedenen 17. Einheitswurzeln entsprechend, das heißt in der Reihenfolge
so erhält man durch Teilsummation von jeder zweiten, jeder vierten, beziehungsweise jeder achten Einheitswurzel aus dieser Auflistung die sogenannten Gaußschen Perioden: zwei 8-gliedrige Perioden mit je 8 Summanden, vier 4-gliedrige Perioden mit je 4 Summanden und acht 2-gliedrige Perioden mit je 2 Summanden. Aufgrund prinzipieller Eigenschaften oder aber durch explizite Berechnung lässt sich dafür zeigen:[5]
- Die beiden 8-gliedrigen Perioden sind Lösungen einer quadratischen Gleichung mit ganzen Koeffizienten.
- Die vier 4-gliedrigen Perioden sind Lösungen von zwei quadratischen Gleichungen, deren Koeffizienten aus den 8-gliedrigen Perioden berechenbar sind.
- Die acht 2-gliedrigen Perioden sind Lösungen von vier quadratischen Gleichungen, deren Koeffizienten aus den 4-gliedrigen Perioden berechenbar sind.
Dabei gilt für die zweigliedrige Periode zur „ersten“ Einheitswurzel .
Der beschriebene Ansatz lässt sich analog für jede Primzahl der Form durchführen. Fünf solche Primzahlen, die „Fermatsche Primzahlen“ genannt werden, sind bekannt: 3, 5, 17, 257, 65537. Daher gehören auch das regelmäßige 257-Eck und das regelmäßige 65537-Eck zu den konstruierbaren Polygonen.
Geometrische Konstruktionen
Konstruktion mithilfe der gaußschen Kurzfassung der Formel
Anlässlich der 150. Wiederkehr des Todestages von Carl Friedrich Gauß am 23. Februar 2005 gab es in Göttingen im Alten Rathaus am Markt vom 23. Februar – 15. Mai 2005 die Ausstellung „Wie der Blitz einschlägt, hat sich das Räthsel gelöst“ Carl Friedrich Gauß in Göttingen. Der Katalog zu dieser Ausstellung, herausgegeben von Elmar Mittler, enthält Aufsätze in diversen Rubriken. Im Abschnitt Mathematik ist der Beitrag 17 gleiche Ecken und Kanten mit Zirkel und Lineal von Hans Vollmayr zu finden.[6] Die im Folgenden dargestellte Konstruktion ist prinzipiell den Kapiteln Das Siebzehneck: die Rechnung[7] und Das Siebzehneck: die Zeichnung[8] entnommen.
Die Kurzfassung der Formel für den Kosinus des Zentriwinkels (siehe Eigenschaften),
erleichtert eine Konstruktion mit Zirkel und Lineal, die mithilfe der Hilfsgrößen, quasi Schritt für Schritt, den Kosinus des Zentriwinkels liefert. Ein möglicher Lösungsweg ist, die Hilfsgrößen zeichnerisch separat in drei Bildern (1 – 3) mit elementaren algebraischen Operationen darzustellen. Dies macht die Konstruktion übersichtlich und allgemein gut nachvollziehbar.
Konstruktion der Hilfsgrößen p und q sowie des Produkts qq
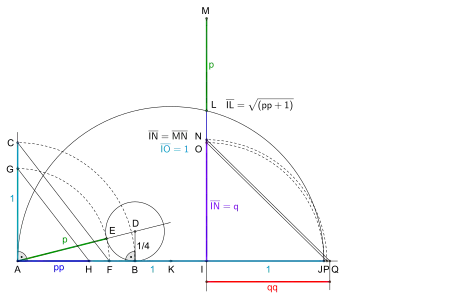
Darin gilt
sowie
Bild (1)
- Ab Punkt eine Halbgerade ziehen, darauf mit Lot auf Strecke in errichten und ab auf Lot übertragen ergibt
- Lot auf in mit Länge ergibt anschließend Halbgerade von durch ergibt
- Kreis um durch ergibt auf Halbgerade, ist Hilfsgröße
- Viertelkreis um durch ergibt und nun mit verbinden, anschließende Parallele zu ab ergibt sowie mit das Produkt
- Zu zweimal die Länge addieren, ergibt und anschließend in halbieren und um über Halbkreis ziehen.
- Lot auf in bis Halbkreis ergibt anschließend zu ab Hilfsgröße addieren, ergibt
- in halbieren ergibt Hilfsgröße
- Viertelkreis um ab ergibt anschließend Viertelkreis um ab ergibt
- mit verbinden, anschließende Parallele zu ab ergibt sowie mit das Produkt
Konstruktion der Hilfsgrößen p' und q'
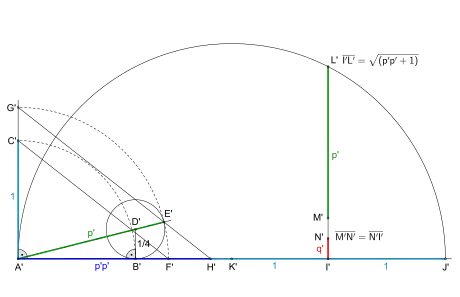
Darin gilt
sowie
Bild (2)
- Ab Punkt eine Halbgerade ziehen, darauf mit Lot auf Strecke in errichten und ab auf Lot übertragen ergibt
- Lot auf in mit der Länge ergibt anschließend Halbgerade von durch ergibt
- Kreis um durch ergibt auf Halbgerade, ist Hilfsgröße
- Viertelkreis um durch ergibt und nun mit verbinden, anschließende Parallele zu ab ergibt sowie mit das Produkt
- Zu zweimal die Länge addieren, ergibt und anschließend in halbieren und um über Halbkreis ziehen.
- Lot auf in bis Halbkreis ergibt anschließend von ab Hilfsgröße subtrahieren, ergibt
- in halbieren ergibt mit Hilfsgröße
Konstruktion der Wurzel aus qq-2q' und des Kosinus des Zentriwinkels μ
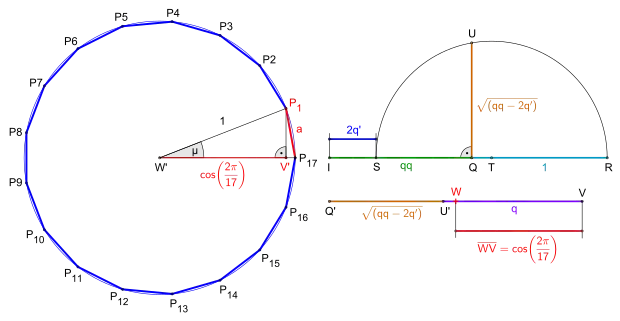
Bild (3)
- Ab Punkt eine Halbgerade ziehen, darauf Produkt aus Bild (1) übertragen ergibt anschließend Länge aus Bild (1) ab übertragen ergibt
- Von die Länge aus Bild (2) ab Punkt subtrahieren ergibt anschließend in halbieren und um über Halbkreis ziehen.
- Lot auf in bis Halbkreis ergibt
- Strecke einzeichnen und dazu Hilfsgröße aus Bild (1) ab addieren ergibt anschließend in halbieren, die Strecke ist der Kosinus des Zentriwinkels des Siebzehnecks.
- Um Punkt Umkreis mit dem Radius (z. B. mit Strecke ) ziehen, anschließend Radius einzeichnen, ergibt
- auf ab übertragen, ergibt
- Lot auf in bis Umkreis ergibt ersten Eckpunkt des entstehenden Siebzehnecks.
- fünfzehnmal gegen den Uhrzeigersinn auf dem Umkreis abtragen und abschließend die benachbarten Ecken verbinden. Somit ist das regelmäßige Siebzehneck fertiggestellt.
Grundsätzlich wäre es auch möglich, den von Gauß zuerst gefundenen (langen) Ausdruck als konstruierte Strecke darzustellen. In der einschlägigen Literatur wird aber keine derartige Lösung beschrieben.
Konstruktion nach Georg Paucker
Eine der ersten geometrischen Konstruktionsanleitungen für das regelmäßige Siebzehneck stammt von Magnus Georg Paucker, der sie 1819 der Kurländischen Gesellschaft für Literatur und Kunst vorlegte, wo sie 1822 veröffentlicht wurde.[9]
Die folgende Konstruktionsanleitung enthält die Konstruktion nach Magnus Georg Paucker.[10] sowie deren Weiterführung bis zum fertigen Siebzehneck. Die in der Originalzeichnung von Paucker enthaltenen Radien und die meisten Diagonalen dienen der Darstellung von in seiner Originalbeschreibung stehenden Formeln und sind für die geom. Konstruktion nicht erforderlich. Sie wurden hier weggelassen.
- Zeichne auf dem Durchmesser pa um den Mittelpunkt m den Umkreis des werdenden 17-Ecks.
- Errichte den Durchmesser pA = pa senkrecht zu pa.
- Halbiere den Radius mp in B.
- Verlängere pa ab p.
- Trage die Strecke AB ab B auf die Verlängerung ab, Schnittpunkt ist C.
- Halbiere pA in D.
- Halbiere pC in E.
- Trage die Strecke ED ab E auf die Verlängerung ab, Schnittpunkt ist F.
- Errichte den Radius mG senkrecht zu pa.
- Halbiere mC in H.
- Trage die Strecke HG ab H auf pa ab, Schnittpunkt ist I.
- Konstruiere den Halbkreis über pF.
- Konstruiere den Halbkreis über pI, Schnittpunkt mit mG ist K.
- Zeichne die Parallele zu mp ab K, Schnittpunkt mit Halbkreis über pF ist L.
- Fälle das Lot von L auf mH, Fußpunkt ist M. Es gilt pM ist die Seite des 34-Ecks.
- Von hier aus zwei Möglichkeiten als Beispiele:
- Ziehe einen Halbkreis um p mit dem Radius pM, damit ergibt sich auf dem Umkreis der Punkt i und ein z. B. mit j bezeichneter Punkt. Die Strecke i j ist die gesuchte Seite des 17-Ecks.
- Trage die Seite i j vierzehnmal auf dem Umkreis ab.
- oder:
- Es gilt auch MF = pc, demzufolge trage MF auf dem Umfang in Richtung Punkt a ab und du erhältst Punkt c.
- Trage ac, also die Diagonale über zwei Seiten, von a beginnend weitere Male auf dem Umfang ab, bis alle Ecken markiert sind.
Jeweils abschließend:
- Verbinde die so gefundenen Punkte zu einem vollständigen 17-Eck.
Konstruktion nach Herbert Richmond
Im Jahr 1825 legte Johannes Erchinger eine Konstruktion der Akademie der Wissenschaften zu Göttingen vor, die Gauß daraufhin in den Göttingischen Gelehrten Anzeigen besprach.[11] Die folgende einfachere Konstruktion stammt von Herbert William Richmond aus dem Jahr 1893.[12]
Ist der Umkreis um das entstehende Siebzehneck mit dem Mittelpunkt O gegeben, kann das Siebzehneck konstruiert werden durch:
- Zeichnen des Durchmessers durch den Mittelpunkt O; Schnittpunkt mit Umkreis ist A, später zusätzlich mit P17 bezeichnet.
- Errichten des Radius senkrecht zu AO auf O bis zum Umkreis; Schnittpunkt mit Umkreis ist B.
- Konstruktion des Punktes I durch Vierteln der Strecke BO; I liegt näher an O.
- Konstruktion des Punktes E durch Vierteln des Winkels OIA.
- Konstruktion des Punktes F mithilfe einer Senkrechten auf EI auf I; Halbierung des 90°-Winkels; Schnittpunkt mit Durchmesser ist F und Winkel FIE ist 45°.
- Konstruktion des Thaleskreises über AF; Schnittpunkt mit BO ist K.
- Zeichnen des Halbkreises um den Mittelpunkt E mit dem Radius EK; Schnittpunkte mit dem Durchmesser sind N3 und N5 (dabei liegt N3 sehr nahe beim Mittelpunkt des Thaleskreises über AF).
- Errichten der Senkrechten auf die Mittelachse ab N3; Schnittpunkt mit dem Umkreis ist der Eckpunkt P3 des Siebzehnecks; der Kreisbogen OAP3 ist somit 3/17 des Umkreisumfanges.
- Errichten der Senkrechten auf die Mittelachse ab N5; Schnittpunkt mit dem Umkreis ist der Eckpunkt P5 des Siebzehnecks; der Kreisbogen OAP5 ist somit 5/17 des Umkreisumfanges.
- Ein vierzehnmaliges Abtragen der Strecke AP3 auf dem Umkreis, ab dem Eckpunkt P3 gegen dem Uhrzeigersinn, ergibt der Reihe nach die Eckpunkte P6, P9, P12, P15, P1, P4, P7, P10, P13, P16, P2, P8, P11 und P14.
- Verbinden der so gefundenen Punkte P1, P2, …, P17, P1 vervollständigt das 17-Eck.
Konstruktion nach Duane DeTemple
Duane W. DeTemple veröffentlichte im Jahr 1991 in der mathematischen Zeitschrift The American Mathematical Monthly eine Konstruktion des Siebzehnecks.[13] Für seine Lösung verwendete er u. a. vier sogenannte Carlyle-Kreise.
- Zeichne die x-Achse und setze darauf den Punkt
- Zeichne um den Einheitskreis mit Radius Schnittpunkte mit sind und
- Konstruiere die y-Achse vom Umkreis des entstehenden 17-Ecks, Schnittpunkt mit ist
- Halbiere den Radius in
- Ziehe den Kreisbogen mit dem Radius um
- Errichte eine Senkrechte auf dem Radius ab Schnittpunkt mit ist
- Ziehe den Carlyle-Kreisbogen um durch (mit ) so, dass er die x-Achse vom Umkreis zweimal trifft, Schnittpunkte sind und
- Halbiere die Strecke in
- Halbiere die Strecke in
- Ziehe den Carlyle-Kreisbogen um ab bis auf die x-Achse, Schnittpunkt ist
- Ziehe den Carlyle-Kreisbogen um ab bis auf die x-Achse, Schnittpunkt ist
- Trage von Punkt aus auf der Geraden ab. Du erhältst Punkt
- Verbinde mit
- Halbiere die Strecke in
- Ziehe den Carlyle-Kreisbogen um ab bis auf die x-Achse, Schnittpunkt ist
- Ziehe den Kreisbogen mit dem Radius um Schnittpunkte mit dem Umkreis sind die Eckpunkte und somit ist die Strecke die erste Seite des gesuchten 17-Ecks.
- Ein vierzehnmaliges Abtragen der Strecke auf dem Umkreis ab dem Eckpunkt gegen den Uhrzeigersinn, ergibt der Reihe nach die Eckpunkte bis
- Verbinde die so gefundenen Punkte und dann ist das 17-Eck vollständig gezeichnet.
Konstruktion nach L. Gérard
Pietro Ermenegildo Daniele, ein italienischer Mathematiker (1875–1949), beschreibt im sechsten Artikel seines Werkes Über die Konstruktionen des regulären Siebzehnecks eine Konstruktion nach L. Gérard[14] mithilfe des Satzes von Mohr-Mascheroni.
Gérards Siebzehneck – allein mit einem Zirkel konstruiert – wurde in Mathematische Annalen (48. Band) im Jahr 1897 veröffentlicht.[15][16]
- Das im nebenstehenden Bild eingetragene farbige Siebzehneck sowie die gepunkteten Verbindungslinien der Eckpunkte, sind nicht Teil der Lösung (alleinige Verwendung des Zirkels), sie sollen lediglich der Veranschaulichung dienen. Um die Erklärungen von Daniele zum mathematischen Hintergrund (§ 4. Die Konstruktion von Gérard, ab Seite 183) nachvollziehen zu können, wurden die Bezeichnungen der Schnittpunkte übernommen. In der folgenden Konstruktion entsteht jeder Schnittpunkt durch das Kreuzen zweier Kreise. Für eine bessere Übersichtlichkeit, ersetzen kurze Kreisbögen die entsprechenden Kreise.
- Konstruktionsbeschreibung
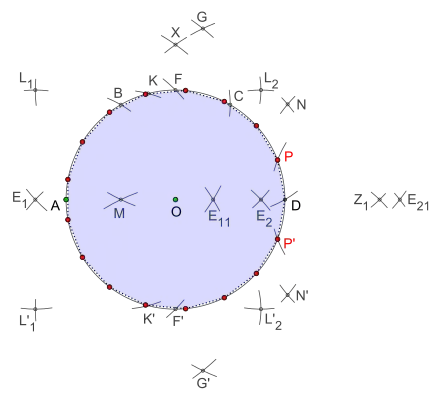
Mohr-Mascheroni allein mit Zirkel konstruiert
Es beginnt mit dem Einheitskreis um den Mittelpunkt Radius . Nun trägt man im Uhrzeigersinn dreimal den Radius auf den Umkreis des entstehenden Siebzehnecks auf, dabei ergeben sich die Schnittpunkte sowie der erste Eckpunkt
Es folgt die Ermittlung des Mittelpunktes vom Radius Zwei Kreisbögen um mit dem Radius und zwei Kreisbögen um mit dem Radius erzeugen die Schnittpunkte und . Je ein Kreisbogen um und mit Radius liefert den Schnittpunkt
Es geht weiter mit dem Bestimmen der noch erforderlichen Schnittpunkte bis
- je ein Kreisbogen um und mit Radius
- und zwei Kreisbögen um mit Radius
- und zwei Kreisbögen um mit Radius
- und je zwei Kreisbögen um und mit Radius
- und je zwei Kreisbögen um und mit Radius sowie zwei Kreisbögen um mit Radius
- je einen Kreisbogen um und mit Radius
- und je zwei Kreisbögen um und mit Radius sowie zwei Kreisbögen um mit Radius
- je ein Kreisbogen um und mit Radius
- und je zwei Kreisbögen um und mit Radius
- je ein Kreisbogen um und mit Radius
Jetzt bedarf es nur noch zweier Kreisbögen um mit Radius , um zwei weitere Eckpunkte und zu erhalten. Die Abstände und entsprechen jeweils einer Seitenlänge des entstehenden Siebenecks.
Abschließend liefern die noch fehlenden 14 Eckpunkte, durch Abtragen des Abstandes auf den Umkreis, ein regelmäßiges Siebzehneck allein mit Zirkel erstellt.
Vorkommen

In der Leipziger Mädlerpassage ist in der Kuppel der Rotunde eine Fensterrose eingelassen, deren Umriss einem Siebzehneck gleicht. Sie misst etwa zwölf Meter im Durchmesser und befindet sich ungefähr auf fünfzehn Meter Höhe.[17] Errichtet wurde die Fensterrose von dem Architekten Theodor Kösser innerhalb seines Projektes Mädlerpassage (1912–1914).
Regelmäßige überschlagene Siebzehnecke
Ein regelmäßiges überschlagenes Siebzehneck ergibt sich, wenn beim Verbinden der siebzehn Eckpunkte jedes Mal mindestens einer übersprungen wird und die somit erzeugten Sehnen gleich lang sind. Notiert werden solche regelmäßigen Sterne mit Schläfli-Symbolen , wobei die Anzahl der Eckpunkte angibt und jeder -te Punkt verbunden wird.
In der folgenden Galerie sind die sieben möglichen regelmäßigen Siebzehnstrahlsterne, auch Heptadekagramme genannt, dargestellt.
- Regelmäßige Siebzehnstrahlsterne







Siehe auch
- Kreisteilung
- Siebzehneck, Konstruktion aus dem Jahr 1818
Literatur
- Godfrey Harold Hardy, E. M. Wright: An Introduction to the Theory of Numbers. Oxford University Press, 2008, ISBN 978-0-19-921986-5, Kapitel 5.8: Construction of the regular polygon of 17 sides, S. 71–77.
- Harold Scott MacDonald Coxeter: Introduction to Geometry. 2. Auflage. Wiley, 1989, ISBN 0-471-50458-0, S. 26–28.
- Karin Reich: Die Entdeckung und frühe Rezeption der Konstruierbarkeit des regelmäßigen 17-Ecks und dessen geometrische Konstruktion durch Johannes Erchinger (1825). In: Rüdiger Thiele (Hrsg.): Mathesis, Festschrift zum siebzigsten Geburtstag von Matthias Schramm. GNT-Verlag, Berlin / Diepholz 2000, S. 101–118.
Weblinks
- Eric W. Weisstein: Heptadecagon. In: MathWorld (englisch).
- Edmund Weitz: Das regelmäßige 17-Eck. In: YouTube. 2017, abgerufen am 27. August 2020.
Einzelnachweise
- H. Maser: Die Teilung des Kreises ..., Artikel 365. In: Carl Friedrich Gauss' Untersuchungen über höhere Arithmetik. Verlag von Julius Springer, Berlin 1889; Göttinger Digitalisierungszentrum, Universität Göttingen, S. 446 ff, abgerufen am 15. März 2018.
- Friedrich L. Bauer: Historische Notizen zur Informatik. Hrsg.: Springer-Verlag. Berlin, Heidelberg 2009, S. 413 (Google Books, Carl Friedrich Gauß, das 17-Eck und MATHEMATICA, Die Methode der Gruppierung [abgerufen am 20. Juli 2018]).
- Hans Vollmayr: 17 gleiche Ecken und Kanten mit Zirkel und Lineal. In: Göttinger Bibliotheksschriften 30 „Wie der Blitz einschlägt, hat sich das Räthsel gelöst“ Carl Friedrich Gauß in Göttingen. Hrsg.: Elmar Mittler. Niedersächsische Staats- und Universitätsbibliothek, Göttingen 2005, ISBN 3-930457-72-5, S. 103 (Das Siebzehneck: die Zeichnung, → „ ... so dass uns am Schluss nur noch die Gleichung ...“ [PDF; abgerufen am 23. Januar 2020]).
- Zitiert nach Jörg Bewersdorff: Algebra für Einsteiger: Von der Gleichungsauflösung zur Galois-Theorie, Springer Spektrum, 6. Auflage 2019, ISBN 978-3-658-26151-1, S. 90, doi:10.1007/978-3-658-26152-8_7.
- Details siehe Bewersdorff, S. 92–96.
- Hans Vollmayr: 17 gleiche Ecken und Kanten mit Zirkel und Lineal. In: Göttinger Bibliotheksschriften 30 „Wie der Blitz einschlägt, hat sich das Räthsel gelöst“ Carl Friedrich Gauß in Göttingen. Hrsg.: Elmar Mittler. Niedersächsische Staats- und Universitätsbibliothek, Göttingen 2005, ISBN 3-930457-72-5, S. 90 ff. (17 gleiche Ecken und Kanten mit Zirkel und Lineal [PDF; abgerufen am 23. Januar 2020]).
- Hans Vollmayr: 17 gleiche Ecken und Kanten mit Zirkel und Lineal. In: Göttinger Bibliotheksschriften 30 „Wie der Blitz einschlägt, hat sich das Räthsel gelöst“ Carl Friedrich Gauß in Göttingen. Hrsg.: Elmar Mittler. Niedersächsische Staats- und Universitätsbibliothek, Göttingen 2005, ISBN 3-930457-72-5, S. 100–102 (Das Siebzehneck: die Rechnung [PDF; abgerufen am 23. Januar 2020]).
- Hans Vollmayr: 17 gleiche Ecken und Kanten mit Zirkel und Lineal. In: Göttinger Bibliotheksschriften 30 „Wie der Blitz einschlägt, hat sich das Räthsel gelöst“ Carl Friedrich Gauß in Göttingen. Hrsg.: Elmar Mittler. Niedersächsische Staats- und Universitätsbibliothek, Göttingen 2005, ISBN 3-930457-72-5, S. 102–103. (Das Siebzehneck: die Zeichnung [PDF; abgerufen am 15. Januar 2019]).
- Magnus Georg Paucker: Geometrische Verzeichnung des regelmäßigen Siebzehn-Ecks und Zweyhundertsiebenundfunfzig-Ecks in den Kreis. In: Jahresverhandlungen der Kurländischen Gesellschaft für Literatur und Kunst. Band 2, 1822, S. 160–219 (Einleitung, Beschreibung S. 187–188). Abgerufen am 20. August 2020.
- Magnus Georg Paucker: Geometrische Verzeichnung des regelmäßigen Siebzehn-Ecks und Zweyhundertsiebenundfunfzig-Ecks in den Kreis. In: Jahresverhandlungen der Kurländischen Gesellschaft für Literatur und Kunst. Band 2, 1822 (Abbildung nach S. 416 in Tafel I, Fig. 12). Abgerufen am 20. August 2020.
- Carl Friedrich Gauß: Göttingische Gelehrte Anzeigen. Band 87, Nr. 203, 19. Dezember 1825, S. 2025–2027 (books.google.de).
- Herbert W. Richmond: A Construction for a regular polygon of seventeen sides. In: The Quarterly Journal of Pure and Applied Mathematics. Band 26, 1893, S. 206–207 (Beschreibung und Abbildung Fig. 6).
- Duane W. DeTemple: Carlyle Circles and the Lemoine Simplicity of Polygon Constructions. (Memento vom 11. August 2011 im Internet Archive). The American Mathematical Monthly, Vol. 98, No. 2 (Feb., 1991), S. 101–104 (JSTOR 2323939) aufgerufen am 3. April 2017.
- Ermenegildo Daniele: Über die Konstruktionen des regulären Siebzehnecks. In: § 4. Die Konstruktion von Gérard. RCIN, S. 171 bzw. 183, abgerufen am 19. Oktober 2021.
- Felix Klein, Walther Dyck, Adolph Mayer: Mathematische Annalen. Inhalt des achtundvierzigsten Bandes. Göttinger Digitalisierungszentrum, 1897, abgerufen am 19. Oktober 2021.
- L. Gérard: Construction du polygone régulier de 17 côtés au moyen du seul compas. In: Mathematische Annalen. Göttinger Digitalisierungszentrum, 8. Juli 1896, S. 390–392, abgerufen am 20. Oktober 2021.
- Anke Beesch: Mädlerpassage in Leipzig. In: Architektur Historische Baukunst mitten in Leipzig. Abgerufen am 3. November 2018.