Satz von Mohr-Mascheroni
Der Satz von Mohr-Mascheroni aus der synthetischen Geometrie besagt, dass jede Konstruktion, die mit Zirkel und Lineal durchgeführt werden kann, bereits mit Zirkel alleine möglich ist. Benannt ist er nach den Mathematikern Georg Mohr und Lorenzo Mascheroni, die ihn unabhängig voneinander bewiesen. Er ist damit das Pendant des Satzes von Poncelet-Steiner.
Geschichte
Erstmals bewiesen wurde der Satz 1672 von Georg Mohr. Sein Beweis geriet aber in Vergessenheit, sodass der Satz 1797 erneut von Lorenzo Mascheroni bewiesen wurde. Erst später wurde Mohrs Beweis durch Johannes Hjelmslev wiederentdeckt, und der Satz nach den beiden Mathematikern benannt. Es folgten eine Reihe von wesentlich einfacheren Beweisen. Die meisten dieser Beweise sind elementargeometrisch, von Jean-Claude Carrega stammt ein algebraischer Beweis der Aussage.
Aussage
Der Satz besagt Folgendes: Gibt es – ausgehend von einer vorgegebenen Menge von Punkten – ein Konstruktionsverfahren, das durch die wiederholte Anwendung der elementaren Konstruktionen 1 bis 5 einen Punkt P konstruiert, so gibt es auch ein Verfahren, das aus derselben Ausgangslage den Punkt P konstruiert, dabei aber nur die Konstruktionen 2 und 5 benutzt. Die elementaren Konstruktionen sind:
- Zu zwei (gegebenen oder konstruierten) Punkten kann die Gerade durch diese beiden Punkte konstruiert werden.
- Zu zwei Punkten kann der Kreis konstruiert werden, der seinen Mittelpunkt im ersten Punkt hat und auf dessen Umfang der zweite Punkt liegt.
- Zu zwei Geraden lässt sich der Schnittpunkt konstruieren (sofern die Geraden nicht parallel sind).
- Zu einer Geraden und einem Kreis lassen sich die Schnittpunkte konstruieren (sofern sie existieren), bzw. der Berührpunkt.
- Zu zwei Kreisen lassen sich die Schnittpunkte bzw. der Berührpunkt konstruieren.
Beweisidee
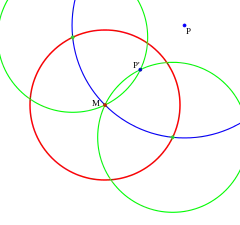
Die meisten Beweise laufen darauf hinaus, Konstruktionsverfahren anzugeben, wie der Schnittpunkt zweier Geraden bzw. die Schnittpunkte einer Geraden mit einem Kreis mit dem Zirkel allein bestimmt werden können, wobei die Geraden nur durch zwei Punkte gegeben sind. Die folgende Beweisidee macht sich dabei die Inversion am Kreis zu Nutze und geht auf August Adler (1863–1923) zurück.[1][2] Die Inversion am Kreis hat die Eigenschaft, dass sie Geraden und Kreise, die nicht durch das Inversionszentrum gehen, auf Kreise abbildet. So kann die Schnittpunktbestimmung auf den Schnitt zweier Kreise zurückgeführt werden, welcher direkt konstruiert werden kann.
Für den Schnittpunkt zweier Geraden muss man dabei Folgendes tun: Gegeben sind vier Punkte A, B, C und D, gesucht ist der Schnittpunkt S der Gerade AB mit der Geraden CD. Zunächst wählt man einen beliebigen Punkt O, der auf keiner der Geraden liegen darf, und zeichnet einen beliebigen Kreis mit O als Mittelpunkt. Dann konstruiert man die Bildpunkte A', B', C' und D' der vier gegebenen Punkte bei Inversion an diesem Kreis und die Kreise durch die Punkte A', B' und O, sowie durch C', D' und O. Diese beiden Kreise sind die Bilder der Geraden AB und CD und schneiden sich außer in O in einem weiteren Punkt S', dem Bildpunkt des gesuchten Schnittpunkts. Den Schnittpunkt S erhält man hieraus durch erneute Inversion.
Analog geht man im Fall des Schnitts von Gerade und Kreis vor. Es reicht also aus, Punkte, Geraden und Kreis allein mit Zirkel an einem gegebenen Kreis zu spiegeln, wozu Konstruktionen bekannt sind. Für die Konstruktion des Bildes eines einzelnen Punktes ist sie unter Kreisspiegelung im Absatz Mit Zirkel allein erläutert.
Konstruktionen von Mascheroni
Problem von Napoleon
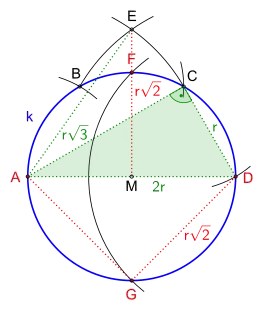
Konstruktion alleinig mit einem Zirkel nach Mascheroni. Darin wird der Wert , quasi der Wert der Diagonalen des Quadrates mit der Seitenlänge r, konstruiert, siehe Animation.
Eine der bekanntesten Konstruktionen von Mascheroni zeigt die Lösung des sogenannten Problem von Napoleon. Darin wird eine gegebene Kreislinie k mit ihrem Mittelpunkt M, unter alleiniger Verwendung eines Zirkels in vier gleichlange Kreisbögen unterteilt,[3] indem man sozusagen den Wert der Diagonalen des Quadrates mit der Seitenlänge r konstruiert.
- Die im nebenstehenden Bild eingetragenen gepunkteten Linien sowie das farbige Dreieck sind für die Lösung der Aufgabe nicht erforderlich, sie sollen lediglich die mathematischen Zusammenhänge veranschaulichen.
Konstruktionsbeschreibung
Es beginnt mit dem Einzeichnen der Kreislinie k mit einem beliebigen Radius r um den Mittelpunkt M. Nach dem Festlegen des Punktes A auf k wird der Radius r dreimal mithilfe kurzer Kreisbögen auf k abgetragen, dabei ergeben sich die Punkte B, C und D. Die Punkte ADC sind Eckpunkte des rechtwinkligen Dreiecks mit der Hypotenuse 2r und der kleinen Kathete r. Nach dem Satz von Pythagoras ergibt sich daraus für die größere Kathete der Wert Diese Länge, sprich Strecke AC, wird nun in den Zirkel genommen und damit jeweils ein kurzer Kreisbogen um Punkt A ab C bzw. um Punkt D ab B geschlagen. Die beiden Kreisbögen erzeugen den Schnittpunkt E. Die Punkte AME sind Eckpunkte des rechtwinkligen Dreiecks mit der Hypotenuse und der kleinen Kathete r. Mithilfe des Satzes von Pythagoras ergibt sich infolgedessen für die größere Kathete der Wert Dies ist auch der Wert der gesuchten Diagonale des Quadrates mit der Seitenlänge r. Abschließend bedarf es noch eines Kreisbogens um den Punkt D mit dem Radius (Strecke ME), der die Kreislinie k in den Punkten F und G schneidet. Somit unterteilen die Kreisbögen MAG, MGD, MDF und MFA die Länge der Kreislinie k in vier gleichlange Teile.
...
August Adler erklärt in seinem Buch Theorie der geometrischen Konstruktionen aus dem Jahr 1906 u. a. drei Konstruktionen von Mascheroni aus dessen Werk „La geometria del compasso“, Pavia 1797, die alleinig unter Verwendung eines Zirkels erstellt wurden. Die erste Konstruktion zeigt wie die Länge einer gegebenen Strecke | AB | in beliebig gleiche Teile teilbar ist, die zweite findet die Mitte einer Strecke, die dritte bestimmt den Mittelpunkt eines Kreises und schließlich die vierte beschreibt in Fünfeck die Konstruktionsbausteine Die Halbierung des Kreisbogens und die Konstruktion der Fünf- und Zehneckseite. Diese vier Zirkelkonstruktionen werden im Folgenden dargestellt und beschrieben.
Länge einer Strecke in beliebig gleiche Teile teilen

- Um die Länge der Strecke | AB | in z. B. drei Teile zu teilen bedarf es der Konstruktion des Punktes C,[4] der gemeinsam mit den gegebenen Punkten A und B (siehe Bild) auf einer virtuellen Linie liegt.
Konstruktionsbeschreibung
Es beginnt mit dem Ziehen des Kreises k um den Punkt A mit dem Radius r = | AB |.
Die folgenden fünf Kreisbögen mit dem gleichen Radius r um die Punkte B, E, F, G und H erzeugen den Schnittpunkt C mit dem Abstand | AC | = 3 • | AB |.
Nun wird um C ein Kreisbogen mit dem Radius r1 = | AC | gezogen, die Schnittpunkte sind D und D'.
Die abschließenden Kreisbögen um die Punkte D und D', jeweils mit dem Radius r = | AB |, schneiden sich in X und liefern somit | AX | = 1/3 • | AB |.
Mitte einer Strecke finden

Durch die Teilung der Strecke AB in zwei gleiche Teile wird deren Mitte bestimmt.[4]
- Das im nebenstehenden Bild eingetragene farbige Dreieck ist für die Lösung der Aufgabe nicht erforderlich, es soll lediglich die mathematischen Zusammenhänge veranschaulichen.
Konstruktionsbeschreibung
Zuerst wird um den Punkt A der Strecke AB der Kreisbogen k1 mit dem Radius AB eingezeichnet.
Der nächste Kreisbogen k2, um den Punkt B mit dem Radius AB, bringt die Schnittpunkte E und E'.
Der Kreisbogen k3 um den Punkt E, durch den Punkt E' mit dem Radius | EE' |, ergibt auf k2 den Schnittpunkt C.
Es folgt der Kreisbogen k4 um den Punkt C, durch den Punkt A mit dem Radius | CA |, er erzeugt die Schnittpunkte D und D'.
Nun zieht man den Kreisbogen k5 um den Punkt D', durch den Punkt A mit dem Radius | D'A |.
Der abschließende Kreisbogen k6 um den Punkt D, durch den Punkt A mit dem Radius | DA | liefert den Schnittpunkt X, der die gesuchte Mitte der Strecke AB markiert.
- Diese Konstruktion ist auch für die Bestimmung der Mitte eines Abstandes zweier Punkte anwendbar.
Mittelpunkt eines Kreises finden
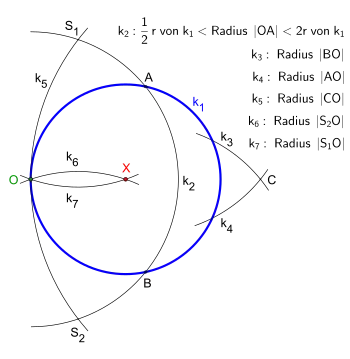
Konstruktionsbeschreibung[2]
Es beginnt mit dem Festlegen des Punktes O auf dem Kreis k1, seine Position ist frei wählbar.
Um den Punkt O wird der Kreisbogen k2 mit einem beliebigen Radius gezogen, es ergeben sich die Schnittpunkte A und B. Damit sich diese Schnittpunkte ergeben bzw. verwertbar sind, muss der Radius |OA| größer als die Hälfte des Radius vom Kreis k1 und kleiner als dessen Durchmesser sein.
Es folgt der Kreisbogen k3 um den Punkt B mit dem Radius | BO |.
Der nächste Kreisbogen k4, um den Punkt A mit dem Radius | AO |, bringt den Schnittpunkt C.
Der Kreisbogen k5, um den Punkt C und durch den Punkt O mit dem Radius | CO |, erzeugt die Schnittpunkte S1 und S2.
Nun zieht man den Kreisbogen k6 um den Punkt S2 durch den Punkt O mit dem Radius | S2O |.
Der abschließende Kreisbogen k7 um den Punkt S1, durch den Punkt O mit dem Radius |S1O | liefert den Schnittpunkt X, der den gesuchten Mittelpunkt des Kreises k1 markiert.
Fünfeck
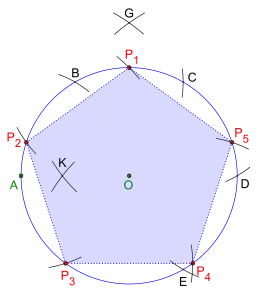
Das Fünfeck ist Beispiel für die Anwendung folgender Konstruktionsbausteine:
Die Halbierung des Kreisbogens [5]
Konstruktion der Fünf- und Zehneckseite [6]
- Das im nebenstehenden Bild eingetragene farbige Fünfeck ist nicht Teil der Lösung (alleinige Verwendung des Zirkels), es soll lediglich der Veranschaulichung dienen.
Konstruktionsbeschreibung
Es beginnt mit dem Festlegen des Radius | AO | für den Kreis, der anschließend um seinen Mittelpunkt O gezogen wird.
Nun werden ab dem Punkt A hintereinander vier Kreisbögen mit dem Radius | AO | auf dem Kreis abgetragen, es ergeben sich die Schnittpunkte B, C, D und E.
Nach Adler folgt jetzt Die Halbierung des Kreisbogens A, B (im nebenstehenden Bild: Kreisbogen OCB):
Hierfür wird zuerst um die Punkte D und A je ein Kreisbogen mit dem Radius | DB | gezeichnet, dabei wird der Schnittpunkt G generiert.
Nun werden um die Punkte C und E je ein Kreisbogen mit dem Radius | OG | gezogen, es ergibt den Schnittpunkt K. Der anschließende Kreisbogen mit dem Radius | OG | um den Punkt A halbiert den Kreisbogen OCB im Punkt P1. Der damit erzeugte Abstand | P1K | ist die Seitenlänge des Fünfecks.
Abschließend noch die Seitenlänge | P1K | fünfmal auf dem Kreis abtragen, danach bilden die Punkte P1, P2, P3, P4 und P5 auf dem Kreis ein regelmäßiges Fünfeck.
Literatur
- Georg Mohr: Euclides danicus. Amsterdam, 1672.
- Lorenzo Mascheroni: Geometrie du compas. Pavia, 1797. (online in der Google-Buchsuche)
- Jean-Claude Carrega: Théorie des corps – La règle et le compas. Editions Hermann, Paris, 2001, ISBN 978-2-7056-1449-2.
- Norbert Hungerbühler: A short elementary proof of the Mohr-Mascheroni theorem. (JSTOR 2974536)
Siehe auch
Weblinks
- Eric W. Weisstein: Mascheroni Construction. In: MathWorld (englisch).
Einzelnachweise
- August Adler: Theorie der geometrischen Konstruktionen. G. J. Göschensche Verlagshandlung, Leipzig 1906, III. Abschnitt, Mascheronische Konstruktionen, § 20. Anwendung des Prinzipes der reziproken Radien, S. 111–112, Fig. 91., S. 125–126 (archive.org [abgerufen am 6. Juni 2018]).
- August Adler: Theorie der geometrischen Konstruktionen. G. J. Göschensche Verlagshandlung, Leipzig 1906, III. Abschnitt, Mascheronische Konstruktionen, § 20. Anwendung des Prinzipes der reziproken Radien, S. 119, Fig. 96., S. 133 (archive.org [abgerufen am 4. Juni 2018]).
- Fritz Schmidt: 200 Jahre französische Revolution Problem und Satz von Napoleon mit Variationen, S. 15. (PDF) In: Didaktik der Mathematik. Bayerischer Schulbuch-Verlag München, 1990, S. 29, abgerufen am 8. Juni 2018.
- August Adler: Theorie der geometrischen Konstruktionen. G. J. Göschensche Verlagshandlung, Leipzig 1906, III. Abschnitt, Mascheronische Konstruktionen, § 16. Vervielfachen und Teilen von Strecken, S. 97–98, Fig. 73., S. 111–112 (archive.org [abgerufen am 10. Juni 2021]).
- August Adler: Theorie der geometrischen Konstruktionen. G. J. Göschensche Verlagshandlung, Leipzig 1906, III. Abschnitt, Mascheronische Konstruktionen, §15. 2. Die Halbierung des Kreisbogens AB, S. 93–94, Fig. 70a. und 70b., S. 107–108 (archive.org [abgerufen am 19. Januar 2019]).
- August Adler: Theorie der geometrischen Konstruktionen. G. J. Göschensche Verlagshandlung, Leipzig 1906, III. Abschnitt, Mascheronische Konstruktionen, §15. 3. Konstruktion der Fünf- und Zehneckseite, S. 94–95, Fig. 71., S. 108–109 (archive.org [abgerufen am 19. Januar 2019]).