Seifenblase
Eine Seifenblase ist ein dünner Film aus Seifenwasser, der eine gewisse Menge Luft oder anderes Gas einschließt und eine hohle Kugel bildet, die häufig irisiert und schillert. Eine Seifenhaut ist ein ebener oder gekrümmter dünner Film, eine Membran aus Seifenwasser, beispielsweise aufgespannt in einem festen Ring. Seifenschaum besteht aus mehreren Seifenblasen. Seifenblasen können bewusst erzeugt werden, zum Beispiel durch das Blasen von Luft in eine auf einem Ring aufgespannte Seifenhaut.

Frisch hergestellte Seifenblasen zeigen elastische Körperschwingung, entlassen unter der Wirkung von Schwerkraft mitunter Wassertropfen, werden von Luftströmungen vertragen oder auch getragen, trocknen zunehmend (wenn die sie umgebende Luft nicht wassergesättigt ist), werden mit der Zeit empfindlicher auf Beanspruchung durch einen Luftstoß oder gar Berührung mit der (trockenen) Oberfläche eines anderen Körpers. Seifenblasen platzen häufig nach kurzer Zeit, mitunter spontan.
Seifenblasen lange in der Luft und am Leben zu erhalten, besondere Figuren oder Größe zu erzielen ist Gegenstand künstlerischer Handarbeit. Seifenblasen sind Untersuchungsgegenstand der Physik, Chemie und Geometrie und dienen als anschauliches Modell für Minimalflächen.
Seifenblasen können händisch-mundgeblasen oder maschinell erzeugt werden. Sie werden als Bühneneffekt und zum Kinderspiel, aber auch für Erwachsene als faszinierend-vergnüglichen Zeitvertreib oder als physikalisch-interessantes Phänomen genutzt.
Wegen dieser leichten Vergänglichkeit wurde ,Seifenblase‘ zu einer Metapher für etwas, das zwar anziehend, aber dennoch inhalts- und gehaltlos ist. Dies spiegelt sich zum Beispiel in der Redewendung „Der Traum zerplatzte wie eine Seifenblase“ oder im Synonym ,Seifenblasenwirtschaft‘ für Bubble Economy.
In der Kunst wird spätestens seit dem Barock die Seifenblase durchgängig ikonographisch als ein Vanitassymbol benutzt und spiegelt sowohl die Schönheit als auch die Flüchtigkeit des menschlichen Lebens wider.
Seifenblasen lösen auf physikalische Weise komplexe räumliche Probleme in der Mathematik, da sie im Gleichgewichtszustand die kleinste Oberfläche zwischen Punkten und Kanten bilden.
Aufbau
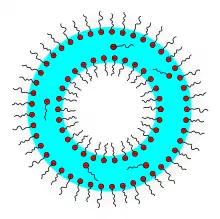
Seifenblasen bestehen aus einem dünnen Wasserfilm, an dem sich innen und außen amphiphile Seifenmoleküle anlagern mit einer dem Wasser zugewandten polaren, hydrophilen Carboxylat-Gruppe und einem dem Wasser abgewandten unpolaren, hydrophoben Alkylrest.
Liposomen weisen einen ähnlichen Aufbau wie Seifenblasen auf: sie sind ebenfalls kugelförmig und auch deren Hülle besteht aus amphiphilen Molekülen, jedoch zeigen hier die hydrophilen Teile der Moleküle nach außen. Selbes bei Biomembranen, bei denen sich das Wasser außen und nicht wie bei Seifenblasen in der Hülle befindet. Liposomen und Biomembranen bestehen beide aus einer Doppellipidschicht.
Vergänglichkeit
Eine Seifenblase entsteht, wenn sich ein dünner Wasserfilm mit Seifenmolekülen vermischt. Beim Aufblasen entsteht eine Kugelform. Infolge des gravitationsbedingten Auslaufens (Drainage) der zwischen den Seifenfilmoberflächen befindlichen Flüssigkeit dünnt eine Seifenblase in ihrem oberen Teil zunehmend aus. Man kann das beobachten, wenn man einen Seifenfilm auf eine Tassenöffnung zieht und dann senkrecht hält. Zudem erfolgt im Laufe des Auslaufprozesses eine Anreicherung von Seifenfilm-stabilisierenden Tensidmolekülen im unteren Bereich der Seifenblase, so dass deren obere Region infolge des relativen Mangels von an die Oberfläche adsorbierten Tensidmolekülen zusätzlich destabilisiert wird. Tatsächlich platzen die meisten Seifenblasen im oberen Teil. Das Verdunsten kann man behindern, indem man die Seifenblase oder einen Seifenfilm in ein Einmachglas „sperrt“. Dadurch verlängert sich die Lebensdauer der Blase erheblich.
Die Schichtdicke der Seifenblase lässt sich beobachten: Spiegelt die Oberfläche in bunten Interferenzfarben, ist die Schichtdicke vergleichbar mit der Wellenlänge des Lichts. Bei abnehmender Schichtdicke wird die Seifenhaut zunächst farblos und zum Schluss dunkel.
In der Schwerelosigkeit überleben Seifenblasen mit etwa einer Minute doppelt so lang wie auf der Erde. Die Blasenwand ist dicker und gleichmäßiger und übersteht auch einen Nadelstich.[1]
Physikalische Grundlagen
Oberflächenspannung
Die Erzeugung von Seifenblasen ist möglich, da die Oberfläche einer Flüssigkeit – in diesem Falle des Wassers – eine Oberflächenspannung besitzt, die zu einem elastischen Verhalten der Oberfläche führt. Häufig wird angenommen, dass die Seife nötig ist, um die Oberflächenspannung des Wassers zu vergrößern. Das Gegenteil ist jedoch der Fall: Die Oberflächenspannung des Seifenwassers ist nur etwa ein Drittel so groß wie die des Wassers. Seifenblasen mit reinem Wasser zu machen ist so schwierig, weil die Oberflächenspannung zu hoch ist, wodurch die Blase sofort zerplatzt. Zusätzlich verlangsamt die Seife die Verdunstung, so dass die Blasen länger halten. Der Gasdruck in einer Seifenblase ist höher als der Druck außerhalb, siehe dazu unter Young-Laplace-Gleichung.
Kugelform
Die Oberflächenspannung ist ebenfalls der Grund für die kugelförmige Gestalt der Seifenblasen. Durch Minimierung der Oberfläche zwingt sie die Blase in diese Form, da von allen möglichen Formen zu einem gegebenen Volumen die Kugel die kleinste Oberfläche aufweist. Ohne äußere Kräfte (insbesondere Schwerkraft in Kombination mit Luftreibung) würden alle Blasen ideale Kugelform besitzen.[2] Aufgrund ihres geringen Eigengewichts kommen Seifenblasen diesem Ideal in der Realität sehr nahe.
Mehrere verbundene Seifenblasen
Wenn zwei Seifenblasen aufeinander treffen, wirken dieselben Prinzipien weiterhin, und die Blasen nehmen die Form mit der kleinsten Oberfläche an. Ihre gemeinsame Wand wölbt sich in die größere Blase hinein, da eine kleinere Seifenblase einen höheren Innendruck besitzt. Wenn beide Seifenblasen gleich groß sind, entsteht keine Wölbung, und die Trennwand ist flach.
Plateaus Regeln besagen, dass beim Zusammentreffen mehrerer Seifenblasen alle Winkel gleich groß sind. In einem Schaum mit vielen Blasen treffen immer jeweils drei Flächen in einem Winkel von 120° zusammen. Hierbei ist die Oberfläche gleichfalls minimal. Durch die gleiche Oberflächenspannung entsteht ein Kräftegleichgewicht. Jeweils vier Kanten treffen sich unter einem Winkel von etwa 109° 28′ 16″ in einem Knoten, auch als Vertex bezeichnet. Diese Regeln wurden im neunzehnten Jahrhundert aufgrund von experimentellen Untersuchungen vom belgischen Physiker Joseph Plateau aufgestellt.
Reflexion und Interferenz
.png.webp)
.png.webp)
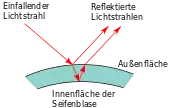
Die schillernden Farben entstehen durch Interferenz von Lichtwellen an der dünnen Seifenhaut. Die Interferenz führt innerhalb eines bestimmten Betrachtungswinkels zur Auslöschung eines Teils des Farbspektrums. Der verbleibende Teil wird farbig wahrgenommen, da nur das komplette Farbspektrum weißes Licht ergibt.
Da die Wand einer Seifenblase eine gewisse Dicke hat, wird einfallendes Licht zweimal reflektiert – einmal an jeder Seite der Wand (siehe rechts). Die leicht unterschiedlichen Weglängen der beiden Lichtstrahlen (und besondere Effekte an der äußeren Wand, s. u.) führen zu einem Gangunterschied zwischen ihnen. Wenn der Gangunterschied genau die Hälfte einer Wellenlänge beträgt, fallen die Wellentäler des einen Strahls mit den Wellenbergen des anderen zusammen (s. zweites Bild). In der Summe ergibt sich Null, also eine Auslöschung der entsprechenden Farbe. Dies nennt man destruktive Interferenz, im Gegensatz zur konstruktiven Interferenz, bei der sich die beiden Strahlen durch einen anderen Gangunterschied positiv überlagern (drittes Bild).
Die tatsächliche Farbe der Seifenblase (d. h. die Wellenlänge des ausgelöschten Lichtes, beziehungsweise die Länge des Gangunterschiedes), ist abhängig von der Dicke der Seifenhaut und des Beleuchtungswinkels der Oberfläche. Die Abhängigkeit von der Schichtdicke kann beobachtet werden, wenn die Seifenblase durch Verdunstung ausdünnt. Mit abnehmender Dicke werden jeweils andere Farben ausgelöscht. Letztlich, wenn die Dicke der Wand kleiner ist als die Hälfte der kleinsten Wellenlänge sichtbaren Lichts, löschen sich keine sichtbaren Lichtwellen gegenseitig aus und es können keine Komplementärfarben mehr beobachtet werden. In diesem Zustand ist die Seifenblasenwand dünner als zwei Zehntausendstel eines Millimeters. Bei noch kleinerer Schichtdicke kann man aufgrund anderer Effekte (s. u.) dunkle Flecken beobachten – sie wird wahrscheinlich im nächsten Moment zerplatzen.
Die Voraussetzung für Interferenzerscheinungen, die Kohärenz der Wellenzüge, ist wegen der Dünne der Schicht erfüllt. Zusätzlich zur unterschiedlichen geometrischen Weglänge trägt hier noch ein anderer Effekt zum Gangunterschied bei:
Die direkt an der Grenzfläche Luft-Seifenhaut (Punkt X im zweiten Bild) reflektierte Welle erfährt einen Phasensprung um bzw. während die Phase der transmittierten Welle auch nach der Reflexion an der Grenzfläche Seifenhaut-Luft (Punkt O im Schaubild) unverändert ist. Hier findet kein Phasensprung statt. Der gesamte Gangunterschied setzt sich aus den unterschiedlichen Weglängen und dem Phasensprung bei der Reflexion an der äußeren Grenzfläche zusammen.
Dies erklärt auch die Verdunkelung der Blase im unmittelbaren Moment vor dem Zerplatzen, wenn die Dicke der Seifenhaut auf einen sehr kleinen Wert gesunken ist: Dies liegt darin begründet, dass die transmittierte Welle, die zuvor den längeren Weg durch die Seifenhaut nahm, nun praktisch keine längere Distanz zurücklegt als die direkte reflektierte Welle und sich deshalb ihre Phase relativ zu dieser nicht ändert. Die reflektierte Welle hat allerdings den oben erwähnten Phasensprung erfahren was zur destruktiven Interferenz (Auslöschung) aller Wellen führt.
Hätte eine Seifenblase überall die gleiche Wandstärke, so würde der Gangunterschied nur durch den Beleuchtungswinkel definiert, und sie würde einen gleichmäßigen Farbverlauf zeigen. Da der Flüssigkeitsfilm in einer Seifenblase, die sich durch eine Luftströmung bewegt, jedoch durch Luftreibung verwirbelt wird, ist die Wandstärke nicht homogen. Unter günstigen Bedingungen kann man diese Verwirbelungen mit bloßem Auge sehen. Schwebt die Seifenblase aber relativ ruhig, treten nur wenige Verwirbelungen auf: Man kann einzelne relativ gleichmäßige Farbbänder beobachten. Die meistens vorhandenen Dickeschwankungen aufgrund der Gravitationskraft sind relativ gleichförmig und stören den gleichmäßigen Farbverlauf nicht prinzipiell.
In einem ebenen Seifenfilm sind diese Farben einfacher sichtbar zu machen. Solch ein ebener Film kann z. B. in einem rechteckigen oder kreisrunden Rahmen aus dünnen Polymer-Fasern oder dünnem Draht geformt werden. Optimale Bedingungen für die Sichtbarkeit der Interferenzfarben sind hier eine indirekte Beleuchtung (z. B. ein Blatt weißes Papier, das von einer Halogenlampe angestrahlt wird) mit 45 Grad Einfallswinkel und Beobachtung in Reflexion bei 45 Grad Ausfallswinkel. Der Hintergrund hinter dem Seifenfilm sollte dunkel sein.
An den Rändern bildet der Film einen Meniskus entweder mit dem Rahmen oder mit einem Flüssigkeits-Reservoir am unteren Ende des Films. In letzterem Fall ist eine Kombination aus Gravitation und Kapillarkraft die treibende Kraft, die eine inhomogene Filmdicke bewirkt.
Verwirbelungen und ästhetische bewegte Muster im Bereich des Meniskus und an den Rändern mit dem Rahmen kommen durch hydrodynamische Instabilitäten zustande, bei denen höchstwahrscheinlich der Marangoni-Effekt eine wichtige Rolle spielt.
Gefrorene Seifenblasen

Die Membran einer Seifenblase kann bei tiefen Temperaturen gefrieren, ohne zu zerplatzen. Das geschieht mit fliegenden Seifenblasen bei Temperaturen unter −10 °C im Freien oder mit anhaftenden Seifenblasen in der Gefriertruhe. Sie sind bis zu 10 Minuten stabil. Manchmal überstehen gefrorene Seifenblasen eine Landung auf hartem und kaltem Untergrund.[3]
Das Gefrieren einer auf Schnee liegenden Seifenblase erfolgt typisch durch Wachsen von fiederartigen Kristallen ab dem als Keim wirkenden anliegenden Schnee und kann etwa 2 Sekunden dauern.[4]
Verwendung
Shows
.jpg.webp)
Seifenblasenshows verbinden Unterhaltung mit künstlerischer Leistung. Hohe Kunstfertigkeit ist dafür ebenso vonnöten wie perfekte Seifenblasenlösungen.
Beispiele üblicher Darbietungen:
- riesige Seifenblasen, die oftmals Gegenstände oder Menschen umfassen,
- Handhaben der Seifenblasen mit bloßen Händen,
- eckige Seifenblasen in der Form von Würfeln, Tetraedern usw.,
- Verbinden von mehreren Blasen zu komplexeren Strukturen oder Skulpturen
- Optisch ansprechende Effekte, zum Beispiel rauchgefüllte Blasen oder Verwendung von Laserlicht,
- mit Helium gefüllte Seifenblasen, die aufwärts schweben,
- Verbindung von Seifenblasen und Feuer.
Seifenblasen in der Mathematik
Ein Seifenfilm formt eine natürliche Minimalfläche. Minimalflächen stehen schon seit dem 19. Jahrhundert im Blickpunkt mathematischer Forschung. Ein wesentlicher Beitrag dazu waren die Experimente des belgischen Physikers Joseph Plateau (vgl. Plateau-Problem).
Ein Beispiel: Schon 1884 wurde von Hermann Amandus Schwarz bewiesen, dass eine kugelförmige Seifenblase die kleinstmögliche Oberfläche eines bestimmten Luftvolumens besitzt. Jedoch erst in den letzten Jahrzehnten wurde mit Hilfe der geometrischen Maßtheorie eine angemessene Sprache für solche Probleme gefunden. Im Jahr 2000 gelang Michael Hutchings, Frank Morgan, Manuel Ritoré und Antonio Ros der Beweis, dass zwei verbundene Seifenblasen (eine sogenannte Doppelblase) zwei verschieden große Luftvolumina mit der kleinstmöglichen Oberfläche umschließen (auch Doppelblasen-Theorem; englisch Double Bubble Theorem).[5]
Seifenblasen in der Architektur
Lange Zeit waren Seifenblasen das einzige Mittel zur zuverlässigen Bestimmung der optimalen Neigung von nicht-trivialen Dachkonstruktionen auf Basis von Seilsystemen und Tragbögen. Dazu wurde die Konstruktion als Rahmen aus Draht geformt und dann in Seifenwasser getaucht. Beim vorsichtigen Herausziehen ergaben sich Kurvenverläufe, die als das experimentell gefundene Optimum der Form zu gelten hatten. Durch Fotografie und andere Methoden wurde das Ergebnis fixiert und auf die zugehörigen Konstruktionszeichnungen übertragen. Die jeweilige Statik für die vorgegebene Form ließ sich dann mit anderen Methoden bestimmen. Ein Beispiel dieser Methodik ist das Olympiagelände München.[6]
Seifenblasen als Spielzeug

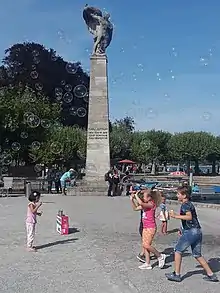
Eine der frühesten künstlerischen Darstellungen von Seifenblasen als Kinderspielzeug findet sich in Pieter Bruegels Gemälde Die Kinderspiele von 1560, woraus sich schließen lässt, dass Seifenblasen bereits seit mindestens 500 Jahren von Kindern zum Zwecke der Unterhaltung verwendet werden. Die Massenproduktion von Seife begann im 19. Jahrhundert, wobei der Seifenhersteller Pears zur Vermarktung insbesondere auch John Everett Millais’ Gemälde Seifenblasen („Bubbles“) nutzte, das dessen Enkel beim Spiel mit Seifenblasen zeigt.
1948 entwickelte der Chemiker Rolf Hein eine neue Formel für ein Waschmittel, das allerdings den Nachteil hatte, zu sehr zu schäumen. Er ließ die flüssige Seife in Flaschen abfüllen, fügte eine Blasring aus einer zum Ring gebogenen feinen Federdrahtwendel mit Stiel hinzu und verkaufte das Produkt unter dem Markennamen Pustefix gezielt als Kinderspielzeug. Seitdem sind zur Herstellung von Seifenblasen vorwiegend Kombinationen von mit Lauge gefüllten Plastikröhrchen und Pustering im Gebrauch.[7]
Literatur
- C. V. Boys: Soap-Bubbles. Their colors and the forces which mold them. Dover Publications, New York 1990, ISBN 0-486-20542-8
- Hannelore Dittmar-Ilgen: Warum platzen Seifenblasen. Physik für Neugierige. Hirzel-Verlag, Stuttgart 2003, ISBN 3-7776-1149-2
- Cyriel Isenberg: The Science of Soap Films and Soap Bubbles. Tieto Books, Clevedon North Somerset 1978, ISBN 0-905028-02-3
- J. Vogel: Gerthsen Physik. Springer Lehrbuch. Springer Verlag, Heidelberg
- C. V. Boys: Seifenblasen und die Kräfte, die sie formen, Natur und Wissen, Band W 13, Desch, München 1961
Weblinks
Einzelnachweise
- science.ORF.at/AFP: Seifenblasen leben im All länger. In: science.ORF.at. 9. Juli 2014, abgerufen am 9. Juli 2014.
- Sam Watons: Researchers test bubble theory in zero gravity, Online auf timesnews.net
- Ashley Leonard: How to Make a Bubble That Doesn't Pop ehow.com, o. J., abgerufen 24. Jänner 2017.
- Gefrierende Seifenblasen im Schnee fotografiert ... pilleus pulcher, google+, 23. Jänner 2017, abgerufen 25. Jänner 2017. – Bilderserie.
- Michael Hutchings; Frank Morgan; Manuel Ritoré; Antonio Ros: Proof of the double bubble conjecture. In: Announc. Amer. Math. Soc., 2000, 6 S. 45–49, pdf.
- Ansgar Mönter: Der mit der Seifenblase. In: nw.de. 17. August 2011, abgerufen am 11. Dezember 2020.
- Die Geschichte der Firma Pustefix. In: pustefix.de. Abgerufen am 6. Juni 2019.
