Stehende Welle

Eine stehende Welle, auch Stehwelle, ist eine Welle, deren Auslenkung an bestimmten Stellen immer bei Null verbleibt. Sie kann als Überlagerung zweier gegenläufig fortschreitender Wellen gleicher Frequenz und gleicher Amplitude aufgefasst werden. Die gegenläufigen Wellen können aus zwei verschiedenen Erregern stammen oder durch Reflexion einer Welle an einem Hindernis entstehen. Bei Wasserwellen siehe Clapotis.

Eine stehende Welle (schwarz) als Überlagerung zweier gegenläufiger Wanderwellen (rot und blau). Die Knoten der stehenden Welle befinden sich an den roten Punkten.

Ein mechanisches Beispiel einer eindimensionalen stehenden Welle ist eine Seilwelle, bei der man ein Seilende auf und ab bewegt und so eine fortschreitende Welle im Seil erzeugt. Ist das andere Seilende befestigt, so wird die Welle dort reflektiert und läuft auf dem Seil zurück. Als Folge sieht man keine fortschreitende Welle mehr, sondern das Seil vollführt eine Schwingung, bei der bestimmte Stellen in Ruhe bleiben (Wellenknoten oder Schwingungsknoten, auch Schnelleknoten), während andere mit großer Schwingungsweite (Amplitude) hin und her schwingen (Wellenbäuche oder Schwingungsbäuche, auch Schnellebauch).

Hintergrund

Der Abstand zweier Wellenknoten oder zweier Wellenbäuche ist die halbe Wellenlänge der ursprünglichen fortschreitenden Wellen.

Bei manchen stehenden Wellen ist eine zweite Größe wichtig, deren Knoten und Bäuche um eine Viertel-Wellenlänge gegenüber denen der ersten Größe verschoben sind. Bei einer stehenden elektromagnetischen Welle sind die beiden Größen die elektrische und die magnetische Feldstärke, bei einer stehenden Schallwelle in einem Blasinstrument der Schalldruck und die Schallschnelle. In diesen Fällen sind die Begriffe Bauch und Knoten daher doppeldeutig; klar sind Bezeichnungen wie Druckbauch, Druckknoten, Schnellebauch (Amplitudenbauch), Schnelleknoten (Amplitudenknoten).

Wenn die stehende Welle mittels zweier gleichphasiger (synchron schwingender) Erreger erzeugt wird, befindet sich ein (Amplituden)bauch genau in der Mitte zwischen ihnen, da die Wellen hier gleichzeitig eintreffen und sich stets gegenseitig verstärken. Eine Viertel-Wellenlänge hiervon entfernt beträgt die Zeitdifferenz des Eintreffens eine halbe Schwingungsperiode. Die Wellen sind hier gegenphasig und löschen sich aus, es entsteht ein (Amplituden)knoten. (Knotenpunkt) Durch Verallgemeinerung dieser Überlegung findet man die Bedingungen:

Bauch: Der Abstand d eines Schwingungsbauches vom Mittelpunkt ist ein Vielfaches der halben Wellenlänge.

d=n\cdot {\frac {\lambda }{2}}\qquad {\text{mit}}\qquad n=0,1,2,\dots

Knoten: Der Abstand d eines Schwingungsknotens vom Mittelpunkt ist ein Vielfaches der halben Wellenlänge plus ein Viertel.

d=\left(n+{\frac {1}{2}}\right)\cdot {\frac {\lambda }{2}}\qquad {\text{mit}}\qquad n=0,1,2,\dots

Die von der Welle transportierte Energie wird durch die Reflexion zurückgeworfen. Auf einem Wellenleiter mit durch vollständige Reflexion entstandener stehender Welle findet daher kein Energietransport statt. Wird die Welle nur teilweise reflektiert, ergibt sich eine Überlagerung von stehender und fortschreitender Welle. In diesem Fall wird Energie transportiert.

Stehende Wellen zwischen zwei Reflektoren

Zwischen zwei Reflektoren können sich nur stehende Wellen mit bestimmten Wellenlängen bilden. Die Frequenzen zu diesen Wellenlängen werden als Eigenfrequenzen oder Eigenresonanzen bezeichnet.

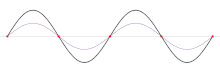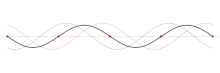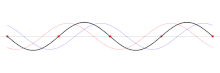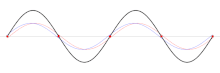
Welche Randbedingung dazu führt, dass die Wellenlängen nicht beliebig sein können, hängt von der Art der betrachteten Welle ab. Beispielsweise muss bei fest eingespannten Enden einer schwingenden Saite an beiden Enden jeweils ein Schwingungsknoten vorliegen, wie in der Abbildung unten gezeigt.

Bei einer stehenden elektromagnetischen Welle gilt, dass die elektrische Feldstärke am reflektierenden Leiter null sein muss, wohingegen die magnetische Feldstärke dort immer einen Schwingungsbauch besitzt. Bei der resultierenden elektromagnetischen Welle sind nun elektrisches Feld und magnetisches Feld um 90° phasenverschoben, wobei das E- und H-Feld der hin- bzw. rücklaufenden Welle phasengleich sind.

Bei einer stehenden (akustischen) Longitudinalwelle tritt an jeder reflektierenden Wand in einem Raum immer ein Schalldruckbauch auf; siehe Raummoden. In der Akustik interessiert überwiegend die Schallfeldgröße als Schalldruck.

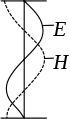Elektrisches Feld und magnetisches Feld bei der Reflexion zu einer stehenden Welle
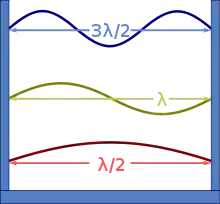Die drei größten Wellenlängen, die bei einer fest eingespannten Saite entstehen.
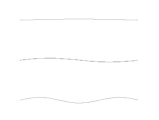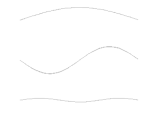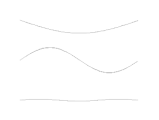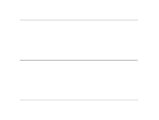Grundschwingung, darunter erster und zweiter Oberton

Stehwellenverhältnis

Ein Maß für den Anteil stehender Wellen auf einem elektrischen Leiter ist das Stehwellenverhältnis (englisch: standing wave ratio = SWR).

Anwendungen

Elektromagnetische Wellen im Hohlraumresonator, z. B. in Teilchenbeschleunigern
Quantenmechanische Erklärung des Wasserstoffatoms
Musikinstrumente (siehe z. B. Saiteninstrumente, Holzblasinstrumente, auch Chladnische Klangfigur).
In Konzertsälen wird nach Möglichkeit vermieden, dass Resonanzen durch stehende Wellen auftreten. Hier wird auf eine für alle Frequenzen gleichmäßig hohe Dämpfung Wert gelegt.
Ein optischer Resonator stabilisiert die Wellenlänge („Farbe“) des Laserlichts.
Stehende Wellen (rhythmische Schwingung) des Wassers in Seen, Buchten oder Hafenbecken bezeichnet man als Seiche (siehe auch Wasserwunder von Konstanz).

Weitere Bilder

Durch die Bewegung der Moleküle können auch größere Teilchen wie Wassertropfen bewegt werden. Die Tropfen sammeln sich in den Schwingungsknoten einer stehenden Welle, die sich aufgrund eines unterhalb der Tropfen angeordneten Schallreflektors ausbildet (Reflektor wurde nicht mitfotografiert). Der Abstand zwischen Wandlerstirnfläche und Reflektor muss passend zur Wellenlänge in Luft gewählt werden.

Treffen kurze Wellenzüge aufeinander, entsteht nur während der Zeit der Begegnung eine stehende Welle.
Für eine kreisförmige stehende Welle muss ein ganzzahliges Verhältnis Umfang/Wellenlänge vorliegen.
Stehende Wellenformen (1–5) im einseitig offenen konischen Rohr
Stehende Welle in der Nachbrennerflamme eines J58-Triebwerks auf dem Prüfstand. Die einzelnen Druckbäuche (Machsche Knoten) sind jedoch nicht Teil einer einzigen stehenden Welle, denn jede aus dem Triebwerk austretende Gasscheibe besitzt eine stehende Welle, die für kurze Dauer anhält und beim passieren der Machschen Knoten immer einen Druckbauch hat.

Siehe auch

Literatur

W. Demtröder: Experimentalphysik 1. 5. Auflage, Springer 2008, ISBN 978-3-540-79294-9
Andreas Friesecke: Die Audio-Enzyklopädie. Ein Nachschlagewerk für Tontechniker. Saur, München 2007, ISBN 978-3-598-11774-9.
Philipp Bohr: Physik. Lehrbuch für die Oberstufe, Norderstedt 2004, ISBN 3-8334-5041-X.
Peter Kaltenbach, Heinrich Meldau: Physik und Funktechnik Für Seefahrer. Friedrich Vieweg & Sohn, Braunschweig 1938.
F. W. Gundlach: Grundlagen der Höchstfrequenztechnik. Springer, Berlin/Heidelberg 1950.

Weblinks

Commons: Stehende Wellen – Sammlung von Bildern, Videos und Audiodateien

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.