Totzeit (Regelungstechnik)

Als Totzeit (auch Laufzeit oder Transportzeit genannt) wird in der Regelungstechnik die Zeitspanne zwischen der Signaländerung am Systemeingang und der Signalantwort am Systemausgang einer Regelstrecke bezeichnet. Jede Änderung des Eingangssignals ruft eine um die Totzeit verzögerte Änderung des Ausgangssignals hervor. Ein System mit Totzeit ohne zusätzliches Zeitverhalten wird auch als Totzeitglied bezeichnet.

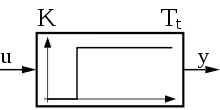
Totzeit-Glied im Strukturbild

Totzeitglieder lassen sich nicht mit gewöhnlichen Differentialgleichungen, sondern nur über das Frequenzverhalten als transzendente Funktionen (nicht algebraisch) beschreiben. Damit erschweren sie die Parametrierung eines Reglers im Regelkreis, weil sich transzendente Funktionen nicht mit gebrochen rationalen Funktionen eines Übertragungssystems zur algebraischen Berechnung kombinieren lassen. Es kann deshalb sinnvoll sein, je nach verwendeter Programmiersprache Totzeitmodelle zu bestimmen, die näherungsweise als gebrochen rationale Funktionen geschrieben werden können.

Die Untersuchung des Frequenzverhaltens von unterschiedlichen linearen Übertragungssystemen mit einem Totzeitglied bei Anwendung des Bode-Diagramms oder der Ortskurve des Frequenzgangs am aufgeschnittenen Regelkreis dient

der Erkennung der Stabilität des geschlossenen Regelkreises,
der Systemanalyse von linearen dynamischen Übertragungsgliedern G(s) und Totzeitverhalten.

Die Darstellung des Übertragungsverhaltens im Zeitbereich von Totzeitgliedern in Verbindung mit linearen und nichtlinearen Übertragungsgliedern im Regelkreis kann zu einem vernünftigen Berechnungsaufwand nur mit der numerischen Mathematik erreicht werden. Dabei werden in Abhängigkeit von einem gegebenen Eingangssignal Wertefolgen im zeitdiskreten Abstand $\Delta t$ berechnet. In einer Grafik lässt sich so ein geschlossenes Zeitverhalten für die Ausgangsgröße $y(t)$ und interessierende Zwischengrößen darstellen.

Grundlagen Totzeitglieder

Zum Verständnis dieses Artikels wird die Kenntnis der Anwendung der Übertragungsfunktion $G(s)$ und der Regelungstechnik vorausgesetzt.

Das Totzeitglied ist ein in der Praxis häufig vorkommendes Übertragungsglied und wirkt meist in Verbindung mit weiteren Verzögerungsgliedern. Es wird durch reine Laufzeit bzw. Transportzeit (Förderband, Rohrleitung) oder bei großen Entfernungen entstehende Signallaufzeiten verursacht. Es verhält sich wie ein P-Glied, dessen Ausgangsgröße verspätet um die Totzeit ankommt, ohne die Eingangsgröße während dieser Zeit zu verzerren. Jede Änderung der Eingangsgröße wirkt um die Totzeit verspätet am Ausgang.[1]

Das Totzeitglied wird nur durch einen Parameter $T_{t}$ beschrieben. Die Phasenverschiebung der Ausgangsgröße zur Eingangsgröße ist proportional der Totzeit und wächst mit dem Produkt $-\omega \cdot T_{t}$ mit steigender Frequenz.

Während Verzögerungsglieder (PT1-Glied) mit steigender Frequenz des Eingangssignals maximal -90° Phasenverschiebung verursachen können, nimmt die Phasenverschiebung bei Totzeitgliedern mit steigender Frequenz ständig zu. Für einen geschlossenen Regelkreis kann diese Phasenverschiebung frühzeitig zu einer Instabilität führen, weil in Abhängigkeit von der Kreisverstärkung die Rückführung der Regelgröße sich von der Gegenkopplung in eine Mitkopplung wandeln kann.

Totzeitglieder sind Nichtphasenminimumsysteme. Ein lineares dynamisches System ist phasenminimal, wenn seine Pole und Nullstellen in der linken s-Halbebene liegen und es keine Totzeit aufweist.

Die Übertragungsfunktion eines linearen dynamischen Systems wird definiert als Quotient der Laplacetransformierten der Ausgangsgröße Y(s) und der Eingangsgröße U(s):

G(s)={\frac {Y(s)}{U(s)}}

Lineare dynamische Übertragungsglieder werden in der Regelungstechnik durch gebrochen rationale Funktionen im Bildbereich (s-Bereich) $G(s)$ beschrieben. Die unabhängige Variable $s=\delta +j\omega$ erlaubt beliebige algebraische Operationen im s-Bereich, ist aber nur ein Symbol für eine vollzogene Laplace-Transformation und enthält keinen Zahlenwert. Zahlenwerte entstehen aus den Koeffizienten a und b der Übertragungsfunktion in Polynomdarstellung, indem die Polynome der Übertragungsfunktion durch Nullstellenzerlegung in Linearfaktoren (Produkte) zerlegt werden.

Beispiel einer Übertragungsfunktion 3. Grades eines linearen dynamischen Systems in Zeitkonstanten-Darstellung:

G_{1}(s)={\frac {Y(s)}{U(s)}}={\frac {K\cdot (T_{v}\cdot s+1)}{s\cdot (T_{1}\cdot s+1)(T_{2}\cdot s+1)}}

Ist in dem System noch ein Totzeitglied $G_{Tt}(s)={\tfrac {Y(s)}{U(s)}}=e^{-s\cdot T_{\mathrm {t} }}$ vorhanden, kann dies als transzendente Funktion multiplikativ der gebrochen rationalen Funktion $G_{1}(s)\cdot G_{Tt}(s)$ angehängt werden.

G_{2}(s)={\frac {Y(s)}{U(s)}}={\frac {K\cdot (T_{v}\cdot s+1)}{s\cdot (T_{1}\cdot s+1)(T_{2}\cdot s+1)}}\cdot e^{-s\cdot T_{\mathrm {t} }}

Im Zeitbereich interessiert das Verhalten der Ausgangsgröße eines Systems für ein gegebenes Eingangssignal. Transzendente Systeme gestalten sich für verschiedene Verfahren der Reglerauslegung ungünstig. Sie können nicht wie gebrochen rationale Systeme algebraisch im s-Bereich behandelt werden.

Derartige als Reihenschaltung zusammengesetzte Systeme können für die Darstellung im Zeitbereich für den Teil der gebrochen rationalen Funktion mit verschiedenen Methoden berechnet werden. Die Totzeitfunktion mit $T_{t}$ wird der berechneten Zeitfunktion grafisch additiv zugeschlagen. Dies gilt nicht für den geschlossenen Regelkreis mit einem Totzeitglied in der Regelstrecke.

Frequenzverhalten des Totzeitgliedes

Im Gegensatz zu den linearen dynamischen Systemen kann ein Totzeitglied nicht mit einer gewöhnlichen Differentialgleichung beschrieben werden. Einen einfacheren Zusammenhang des Ein-/Ausgangsverhaltens ergibt sich im Bildbereich als Übertragungsfunktion $G(s)$ .

Die Funktionalbeziehung eines Totzeitgliedes im Zeitbereich lautet:

\displaystyle y(t)=u(t-T_{\mathrm {t} })

Das Eingangssignal erscheint um die Totzeit verzögert unverändert am Ausgang. Daraus ergibt sich die Übertragungsfunktion im Bildbereich:

G(s)={\frac {Y(s)}{U(s)}}=e^{-s\cdot T_{\mathrm {t} }}

Die Sprungantwort ergibt sich zu:

a(t)=\sigma (t-T)={\begin{cases}0,&t<T\\1,&t\geq T\end{cases}}

Zur Berechnung der Phasenverschiebung wird die Übertragungsfunktion $G(s)$ auf der imaginären Achse des Bildbereichs (welche dem Frequenzverhalten entspricht) betrachtet.

G(s=0+j\omega )=e^{-j\omega \cdot T_{\mathrm {t} }}

Der Phasenwinkel kann jetzt direkt abgelesen werden (siehe hierzu auch Eulersche Identität).

\varphi (\omega )=-\omega \cdot T_{\mathrm {t} }

Mit $\omega =2\pi f$ ergibt sich daraus die Phasenverschiebung in Abhängigkeit von der Frequenz:

\varphi (f)=-2\pi f\cdot T_{\mathrm {t} }

Ein reines Totzeitglied hat die Verstärkung 1 bzw. die Dämpfung D = 0 [dB]. Die Phasenverschiebung zwischen Eingangssignal $u(t)$ und Ausgangssignal $y(t)$ erhöht sich bei steigender Frequenz nacheilend um $\varphi (\omega )=-\omega \cdot T_{\mathrm {t} }$ , also proportional zur Frequenz.

Mit steigender Totzeit als Parameter wird ein Regelkreis instabil, was zur Reduzierung der Kreisverstärkung zwingt. Damit wird der Regelkreis träge gegenüber Führungsgrößenänderungen und Störgrößeneinflüssen.

Stabilitätsbetrachtung eines aufgeschnittenen Regelkreises für Systeme mit Totzeit

Die klassische Darstellung eines dynamischen Systems mit Totzeit ist das Bode-Diagramm und die Ortskurve des Frequenzgangs. Beide grafischen Verfahren eignen sich zur Stabilitätsbestimmung mittels eines aufgeschnittenen Regelkreises für den geschlossenen Regelkreis. Die Übertragungsfunktion $G(s)$ mit $s=\delta +j\cdot \omega$ kann jederzeit ohne Informationsverlust in den Frequenzgang $G(j\omega )$ oder $F(j\omega )$ übertragen werden.[2]

Beispiel eines Bode-Diagramms für 2 PT1-Glieder mit den Eckfrequenzen bei

\omega _{E}=10^{3}

und

\omega _{E}=10^{6}

.

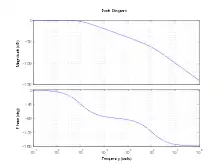
Stabilitätsbedingung im Bode-Diagramm mit dem vereinfachten Stabilitätskriterium von Nyquist

Beim Bode-Diagramm werden Betrag und Phasenwinkel in zwei getrennten Diagrammen aufgetragen, als Amplitudengang und Phasengang. Das Bode-Diagramm hat einen logarithmischen Maßstab. Beim Amplitudengang (doppelt logarithmisch) ist der Betrag F(jω) auf der Ordinate, die Kreisfrequenz ω auf der Abszisse aufgetragen. Beim Phasengang ist der Phasenwinkel (linear) auf der Ordinate, die Kreisfrequenz ω auf der Abszisse (logarithmisch) aufgetragen.

Die Vorteile dieses Verfahrens sind das unmittelbare Einzeichnen der Asymptoten als Geraden des Amplitudengangs, die bequeme Multiplikation durch logarithmische Addition, das direkte Ablesen der Zeitkonstanten und das schnelle Erkennen der Stabilität des geschlossenen Regelkreises. Bei phasenminimalen Systemen ist der Phasengang aus dem Amplitudengang berechenbar und braucht nicht unbedingt gezeichnet zu werden. Dies gilt nicht für Systeme mit einem Totzeitglied.

Frequenzverhalten von Regelkreisgliedern:

Ein PT1-Verzögerungsglied zeigt beim Amplitudengang mit steigender Frequenz $\omega$ ab der Eckfrequenz (Schnittpunkt der Asymptoten) ein um 45 ° abfallendes Amplitudenverhältnis. Der Phasengang des sinusförmigen Ausgangssignals ist gegenüber dem sinusförmigen Eingangssignal nacheilend um maximal φ = -90 ° verschoben.
Ein PD1-Glied zeigen beim Amplitudengang mit steigender Frequenz $\omega$ ab der Eckfrequenz ein um 45 ° steigendes Amplitudenverhältnis. Der Phasengang des sinusförmigen Ausgangssignals ist gegenüber dem sinusförmigen Eingangssignal voreilend um maximal φ = 90 ° verschoben.
Ein I-Glied zeigt beim Amplitudengang mit steigender Frequenz $\omega$ eine linear mit φ = 45 ° abfallende gerade Linie als Amplitudenverhältnis. Ein I-Glied zeigt beim Phasengang mit steigender Frequenz eine zunehmend auf φ = -90 ° nacheilende Phasenverschiebung.
Ein Totzeitglied zeigt beim Amplitudengang mit steigender Frequenz $\omega$ immer das Amplitudenverhältnis mit der Verstärkung 1. Der Phasengang des Totzeitgliedes steigt proportional mit der Frequenz $\omega$ nacheilend bis ins Unendliche.

Das Stabilitätskriterium ist aus dem Stabilitätskriterium von Nyquist abgeleitet:

Ein geschlossener Regelkreis ist stabil, wenn die nacheilende Phasenverschiebung φ vom Ausgangs- zum Eingangssignal des offenen Kreises bei der Kreisverstärkung K = 1 und φ > −180° beträgt. Die Dämpfung des geschlossenen Kreises wird umso günstiger, je größer der Phasenabstand zu der −180° -Linie beträgt. Dieser Abstand, der oberhalb der – 180°-Linie liegt, nennt man Phasenrand oder auch Phasenreserve und sollte bei etwa 50° ±10° liegen.

Anmerkung: Ist der Amplitudengang auf der Ordinate in dB (Dezibel) aufgetragen, entspricht 0 dB dem Amplitudenverhältnis 1. Der Wert 20 dB entspricht dem Amplitudenverhältnis 10.

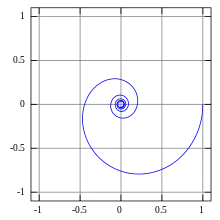
Nyquistdiagramm des PT₁T_t-Glieds eines aufgeschnittenen Regelkreises.

Stabilitätsbedingung mit der Ortskurve des Frequenzgangs

Der Frequenzgang $G(j\omega )$ ist eine komplexe Größe und wird zur grafischen Darstellung in Realteil $\operatorname {Re} (G)$ und Imaginärteil $j\cdot \operatorname {Im} (G)$ getrennt.

Die Frequenzganggleichung (Frequenzgang) des aufgeschnittenen Regelkreises wird nach Realteil und Imaginärteil aufgelöst und in ein Koordinatensystem eingetragen. Die senkrechte Achse zeigt die Daten der Imaginärteile, die waagerechten Achse die Realteile. Nach Nyquist lautet die Stabilitätsbedingung:

Wird beim Durchlaufen der Ortskurve des aufgeschnittenen Regelkreises $F_{0}(j\omega )$ in Richtung steigender Werte von $\omega$ der kritische Punkt (-1; j0) auf der linken (negativen) Seite der Achse der Realteile nicht umschlungen bzw. berührt, ist der geschlossene Regelkreis stabil. Aus praktischen Erwägungen sollte der kritische Punkt (-1; j0) auf (-0,5; j0) verlegt werden, um eine gewisse Stabilitätsreserve zu erzielen.

Die in der Abbildung dargestellte Ortskurve des Frequenzgangs eines Beispiels für den aufgeschnittenen Regelkreis:

G_{0}(j\omega )={\frac {K_{P}}{T\cdot j\omega +1}}\cdot e^{-j\omega \cdot T_{t}}

zeigt laut Abstand von dem kritischen Punkt (-1; j0) der Abszisse des Realteils von 0,5 einen stabilen geschlossenen Regelkreis. Die P-Verstärkung $K_{p}=1$ ist auf der Abszisse direkt ablesbar und entspricht dem Abstand der Punkte $\omega =0(+1;j0)\to \omega =\infty (0;j0)$ .

Anmerkung: Die Ortskurve für ein einzelnes Totzeitglied macht im s-Diagramm mit steigender Frequenz unendlich viele Umläufe auf einer Kreisbahn mit dem Radius $F(j\omega )=1$ . Die Reihenschaltung eines Totzeitgliedes mit einem PT1-Glied (Halbkreis im 4. Quadranten) ergibt durch Addition der beiden Ortskurven den spiralförmigen Verlauf.

Grundlagen der numerischen Berechnung von dynamischen Übertragungssystemen

Relativ einfache Übertragungssystem-Strukturen mit nichtlinearen Elementen sind durch konventionelle Rechenmethoden im kontinuierlichen Zeitbereich nicht mehr geschlossen lösbar. Mit handelsüblichen Personal-Computern kann das Verhalten beliebig vermaschter Systemstrukturen mittels numerischer Berechnung relativ einfach ermittelt werden.

Mit der Simulation eines mathematischen Modells eines Übertragungssystems bzw. eines Regelkreises ergibt sich die Möglichkeit, mit geeigneten Testsignalen eine Systemanalyse oder eine Systemoptimierung durchzuführen.
Der Vorteil der Simulation an einem Modell liegt auf der Hand. Es werden keine technischen Anlagen gefährdet bzw. benötigt. Der Zeitfaktor spielt keine Rolle, es können sehr schnelle oder sehr langsame Prozesse optimiert werden. Voraussetzung ist die mathematische Beschreibung eines gut angenäherten Modells der meist technischen Regelstrecke.
Zur numerischen Berechnung des Zeitverhaltens regelungstechnischer Anlagen mit Totzeit existieren bezüglich der Analyse und Optimierung von Systemen bei Anwendung kommerzieller Programme oder einfacher Programme mit Differenzengleichungen keine anderen Alternativ-Verfahren.

Für die Durchführung der Berechnung von Übertragungssystemen oder der Simulation von Regelkreisen bieten sich käufliche Rechenprogramme an. Mit den bekannten Programmen wie Matlab und Simulink stehen umfangreiche Befehlssätze für die theoretische Modellierung von dynamischen Systemen und vielen speziellen regelungstechnischen Befehlen zur Verfügung.

Alternativ können mit selbst erstellten beliebigen Rechenprogrammen bei Anwendung von Differenzengleichungen in Verbindung mit logischen Operatoren sehr effiziente Regelkreis-Simulationen durchgeführt werden.[3] Dabei sind relativ geringe mathematische Kenntnisse erforderlich.

Die numerische Berechnung erlaubt tabellarisch und grafisch eine völlige Durchsicht des inneren Bewegungsablaufs dynamischer Übertragungssysteme. In Verbindung mit logischen Programmbefehlen und Wertetabellen lassen sich nichtlineare, begrenzende und totzeitbehaftete Systeme simulieren.

Werden die Differenziale der Ausgangsgröße y(t) einer Differenzialgleichung durch kleine Differenzenquotienten $\Delta y/\Delta t$ mit $\Delta t$ als diskretisierte Zeit ersetzt, entsteht eine numerisch lösbare Differenzengleichung in Annäherung an die Differenzialgleichung. Zweckmäßig ist die Umwandlung linearer Elementarsysteme (Übertragungsfunktionen wie I-, PT1-, D-, PD1-Glieder) in Differenzengleichungen. Diese können je nach Lage der Funktionsblöcke im Signalflussplan mit nichtlinearen Systemen oder Systemen mit Totzeit und deren numerischen Berechnungsmethoden rekursiv behandelt werden.

Die numerische Berechnung der Differenzengleichungen der einzelnen Regelkreisglieder erfolgt tabellarisch schrittweise im Abstand der diskreten Zeit $\Delta t$ . Die Gleichungen werden mit $k=(0;1;2;3\cdots k_{\mathrm {max} })$ Berechnungsfolgen wiederholt berechnet. Zu Beginn jeder Berechnungszeile steht die Regelabweichung $e_{(k)}=w_{(k)}-y_{(k-1)}$ . Jede Ausgangsgröße $y_{(k)}$ wird zur nächsten Berechnungsfolge der gleichen Zeile zur Eingangsgröße. Jede einzelne Differenzengleichung für ein bestimmtes Regelkreisglied bezieht sich auf die gleiche Differenzengleichung einer zurückliegenden Folge $y_{(k-1)}$ .

→ Ausführliche Details siehe Wikibooks, „Einführung in die Systemtheorie“, Kapitel: Numerische Berechnung dynamischer Systeme

→ siehe auch numerische Berechnung Differenzengleichung (Differenzenverfahren)

Modelle von Regelstrecken mit Ersatztotzeit

Das Einschwingverhalten der Regelgröße eines Regelkreises mit Totzeit oder Begrenzungseffekten für ein gegebenes Eingangssignal lässt sich – abgesehen von kommerziell erwerbbaren PC-Programmen – nur numerisch über Differenzengleichungen in Kombination mit logischen Befehlen berechnen.

Numerische Berechnungen (Simulationen) werden tabellarisch ausgeführt. Eine Zeile enthält alle Funktionen (Gleichungen) der Teilsysteme eines Regelkreises. In jeder Spalte steht eine Gleichung für ein Teilsystem. Alle Zeilen sind bis auf den Zeitmaßstab $k_{i}\cdot \Delta t$ identisch. Die Folge $k=(0;1;2;3;\dots ;k_{\mathrm {max} })$ einer Zeile bestimmt ein Teilergebnis des Gesamtsystems.

Differenzengleichungen können mit jeder Programmiersprache berechnet werden. Bei Anwendung der Tabellenkalkulation – Vorteil ist die Vermeidung von Programmfehlern und unmittelbare grafische Darstellung der gesuchten Größe – kann für die Berechnung der Totzeit die INDEX-Funktion innerhalb einer Matrix (hier eine Spalte) alle beliebigen Spaltenwerte anfahren.

Für die Berechnung der INDEX-Funktion zur Auswahl einer Zelle im Matrixbereich mit S = Spalte, Z = Zeile gilt:

{\text{Zahlenwert in Zelle}}(Z,S)=\mathrm {INDEX{\bigg [}Matrixbereich(Z_{ni},S_{ni});Zeile(Z_{ni});Spalte(S_{ni}){\bigg ]}}

und abgewandelt zur Totzeitberechnung auf eine Spalte:

{\text{Zahlenwert in Zelle}}(S_{i})=\mathrm {INDEX{\bigg [}\underbrace {(S_{\mathrm {min} }:S_{\mathrm {max} })} _{\text{Spaltenbereich}};\underbrace {(S_{\mathrm {max} })-(S_{\mathrm {min} })-{\frac {T_{t}}{\Delta t}}} _{\text{Bezug}}{\bigg ]}}

Für die numerische Berechnung mit der Tabellenkalkulation enthalten die Zellen meist Gleichungen und bilden stets Zahlenwerte ab. Die Zellposition ist durch einen Buchstaben und eine Zeilennummer definiert. Die Gleichungen beginnen mit einem Gleichheitszeichen (=) und enthalten ausschließlich die Adressen von Zellen und sind mit mathematischen Operatoren verknüpft. Die Variablen sind in einem Eingabefeld abgelegt und enthalten eine direkte Adressierung. Die Gleichungen in den Zellen einer Zeile werden von links nach rechts und bei den Zeilen von oben nach unten berechnet und beziehen sich auf die links liegenden Zelleninhalte durch Angabe der Adresse (Buchstabe und Zeilennummer).

Bei der Kopie einer Gleichung einer Zelle in die darunter liegenden Zellen mit dem Befehl „Kopie“, z. B. 1000-fach, ändern sich automatisch die Adressen in alphanumerischer Reihenfolge. Es handelt sich hier um eine relative Adressierung.

Die in der Gleichung enthaltenen Variablen wie ${T_{t}}$ und $\Delta t$ benötigen ihre Werte aus einem Eingabefeld mit direkter Adressierung.

Beispiel der direkten Adressierung der Zelle B2: Eingabefeld Zelle $\mathrm {B2\to \$B\$2}$ .

Beispiel einer Gleichung zur Totzeit-Berechnung in der Spalte K mit Bezug auf Spalte J mit 2 direkten Variablen:

=\mathrm {INDEX{\bigg [}J100:J400;300-\$B\$16/\$F\$15{\bigg ]}}

.

Grenzwert der Totzeit-Eingabe: Die Zelle K400 enthält zur Totzeitberechnung die INDEX-Funktion für die Folge k = 0, also die 1. Zeile der Systemberechnung. Für den in der INDEX-Gleichung angegebenen Bezug mit den Variablen $T_{t}=2{,}99$ [s] und $\Delta t=0{,}01$ [s] kann maximal eine Totzeit $T_{t}=2{,}99$ [s] berechnet werden. Bei größeren Totzeiten muss der Spaltenbereich erweitert werden, anderenfalls entstehen negative Bezüge mit einer Fehlermeldung.
Leere Zellen oberhalb der Eingangsgrößen: Die Zellen der Spalte unterhalb J400 enthalten die Zahlenwerte der Eingangsgrößen u(t). Oberhalb der Zelle der Spalte J400 dürfen in den Zellen für den angegebenen Spaltenbereich J100 bis J400 keine Zeichen stehen, sie repräsentieren die Totzeit $y(t)=0$ .
Totzeitbereich für $T_{t}=0$ : Steht in der Zelle J400 als Eingangsgröße ein Zahlenwert, weisen für eine Totzeit $T_{t}=2$ [s] die Zellen K400 bis K600 den Zahlenwert Null aus.

Soll für die mathematische Beschreibung des Totzeitgliedes die Form als gebrochen rationale Funktion gewünscht sein, sind die nachfolgenden Annäherungsmodelle möglich:

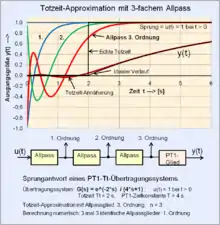Totzeitapproximation mit einem Allpass 3. Ordnung in Reihe mit einem PT1-Glied.

Annäherung an das Verhalten eines Totzeitgliedes durch Allpass-Glieder als Ersatztotzeit

Die Padé-Approximation der Totzeit bringt bereits bei drei identischen Allpassgliedern (n = 3) gute Ergebnisse der Totzeit-Annäherung.[4]

Der Allpass mit einem PD-Glied im Zähler mit einer positiven Nullstelle kann wie folgt in bekannte Teilsysteme 1. Ordnung als PT1-Glied und D-Glied zerlegt werden:

Beispiel von drei identischen Allpassgliedern in Reihenschaltung mit dem Proportionalfaktor K = 1:

G_{T_{t}M1}(s)=\left({\frac {1-{\frac {T_{t}}{2n}}\cdot s}{1+{\frac {T_{t}}{2n}}\cdot s}}\right)^{n}\qquad {\text{mit }}n\to \infty

Damit die positive Nullstelle verschwindet, wird der Zähler des Allpasses wie nachfolgend dargestellt zerlegt.

Beispiel: Wählt man eine Ersatztotzeit mit 3 Allpass-Gliedern und $T_{t}$ = 2 [s]:

G_{T_{t}M1}(s)\approx {\biggl (}{\frac {1-0{,}333\cdot s}{1+0{,}333\cdot s}}{\biggr )}^{3}=K\cdot {\biggl (}{\frac {1}{1+0{,}333\cdot s}}-{\frac {0{,}333\cdot s}{1+0{,}333\cdot s}}{\biggr )}^{3}

Das nebenstehende grafische Bild zeigt die Sprungantwort eines Allpassgliedes 3. Ordnung als Totzeitmodell $T_{tM}=2[s]$ in Reihenschaltung mit einem PT1-Glied $G(s)={\frac {1}{4\cdot s+1}}$ . Das Zeitverhalten der Sprungantwort des Gesamtsystems wurde numerisch über die jedem Einzelsystem zugeordnete Differenzengleichung berechnet.

Annäherung an das Verhalten eines Totzeitgliedes durch PTn-Glieder als Ersatztotzeit

Bereits ab n = 5 PT1-Gliedern bei gleichen Zeitkonstanten lässt sich eine gute Annäherung an ein Totzeitglied erreichen.

Die Sprungantwort eines Totzeitmodells mit 5 PT1-Gliedern mit der Modellzeitkonstante $T_{tM}={\tfrac {T_{t}}{5}}$ zeigt zwar noch beträchtliche Unterschiede im Vergleich mit einem Totzeitglied. Wird das Totzeitmodell im Vergleich mit einem Totzeitglied in je einem Regelkreis mit einem I-Regler gleicher Kreisverstärkung eingebunden, reduzieren sich diese Unterschiede im Zeitverhalten.

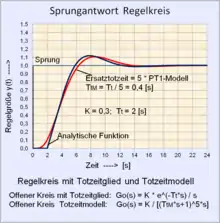
Sprungantworten eines Regelkreises mit I-Regler, PTn-Totzeitmodell und alternativ Totzeitglied.

G_{T_{t}M2}={\frac {1}{\left({\frac {T_{t}}{n}}\cdot s+1\right)^{n}}}\qquad {\text{mit }}n\to \infty

Beispiel:

Wählt man eine Ersatztotzeit mit 5 PT1-Gliedern und $T_{t}$ = 2 [s]:

G_{T_{t}M2}(s)\approx {\frac {1}{(0{,}4\cdot s+1)^{5}}}

Das nebenstehende grafische Bild zeigt die Sprungantwort eines Regelkreises mit einer Regelstrecke für ein Totzeitmodell im Vergleich mit einem Totzeitglied.

Daten Regelkreis: Totzeit $T_{t}=2[s]$ , I-Regler $K=0{,}3$ .

Der aufgeschnittene Regelkreis mit dem Totzeitglied $e^{-s\cdot T_{\mathrm {t} }}$ lautet:

G_{0}(s)={\frac {0{,}3\cdot e^{-s\cdot 2}}{s}}

Der aufgeschnittene Regelkreis mit der Ersatztotzeit lautet:

G_{0M}(s)={\frac {0{,}3}{s\cdot (0{,}4\cdot s+1)^{5}}}

Gezeigt wird der Verlauf der Regelgröße mit dem Totzeitmodell und der analytischen Funktion der Totzeit.

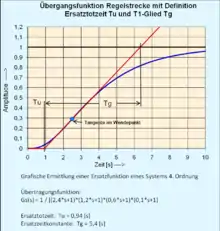
Streckenparameter einer Sprungantwort durch die Tangente am Wendepunkt

Systemanalyse einer Regelstrecke mit Totzeit

Die Sprungantwort hat den Vorteil der einfacheren Durchführung und des höheren Bekanntheitsgrades des zu erwartenden Ergebnisses. Die zeitunabhängige Streckenverstärkung $K_{S}$ kann bei Regelstrecken mit Ausgleich im statischen Zustand direkt abgelesen werden. Das Zeitverhalten der Strecke kann durch ein Modell der Totzeit und ein Modell des S-förmigen Anstiegs des Einschwingvorgangs bestimmt werden.

Folgende Anforderungen werden an die Modellregelstrecke für eine Regelstrecke mit Ausgleich gestellt:

Die Sprungantwort der Modellregelstrecke soll weitgehend deckungsgleich mit der analytischen Funktion der Regelstrecke sein.
Die Modellregelstrecke soll eine bestimmte Form der Übertragungsfunktion aufweisen, die sich mit einem guten linearen Standardregler – beispielsweise einem PID-Regler – leicht für eine Parametrierung des Reglers eignet.
Das Verfahren soll für Regelstrecken ab 2. Ordnung mit und ohne Totzeit anwendbar sein.

Ein PID-Regler in Produktdarstellung (Reihenschaltung) kann 2 PT1-Verzögerungen kompensieren. Deshalb wird folgende leicht zu bestimmende Form der Modellregelstrecke gewählt, die aus einer Reihenschaltung eines schwingungsfreien PT2-Glied und einem Totzeitglied besteht:

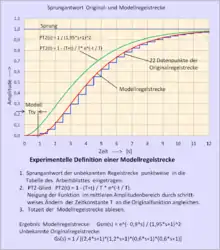
Sprungantwort einer Regelstrecke 4. Ordnung mit dominanter Zeitkonstante und deren Modellregelstrecke 2. Ordnung mit Totzeitglied

Übertragungsfunktion Modell:

G_{SM}(s)={\frac {e^{-T_{u}\cdot s}}{(T_{M}\cdot s+1)^{2}}}

Folgende Vorgänge sind in Verbindung mit einem Personal Computer vorzunehmen:

Die Daten der Sprungantwort des Systems werden in ein Diagramm y(t) = f(t) eingetragen,
Eine Tangente wird am Wendepunkt der aufgezeichneten Sprungantwort angelegt und die Ersatztotzeit = Verzugszeit $T_{u}$ am Schnittpunkt zur Abszisse abgegriffen.
Der PC sollte mit einem beliebigen Rechenprogramm die Sprungantwort von zwei PT1-Gliedern über Differenzengleichungen erzeugen können,
Die Modellübertragungsfunktion $G_{SM}(s)={\tfrac {e^{-T_{u}\cdot s}}{(T_{M}\cdot s+1)^{2}}}$ wird nach der heuristischen Methode „Versuch und Irrtum“ solange mit dem Parameter $T_{M}$ variiert, bis der S-förmige Anstieg der Sprungantwort mit der Antwort des Modells übereinstimmt.
Damit sind die Ersatztotzeit $T_{tE}=T_{u}$ und die Ersatzzeitkonstanten des PT2-Gliedes $T_{M}$ gegeben. Numerische Berechnungen ergeben eine sehr gute Übereinstimmung des Zeitverhaltens der Sprungantwort der Regelstrecke mit dem dargestellten Modell.

→ Ausführliche Details siehe Regelstrecke#Identifikation einer Regelstrecke mit Ausgleich und Totzeit durch die Sprungantwort

Regelung einer Regelstrecke mit Totzeit und Verzögerungsgliedern

Häufig wird in der Fachliteratur die „Regelbarkeit“ einer Regelstrecke mit steigender Totzeit gegenüber weiteren Verzögerungsgliedern als schwierig dargestellt. Tatsächlich ist die Regelung einer Regelstrecke mit großem Totzeitanteil genauso einfach zu regeln wie bei kleinem Totzeitanteil, jedoch ist die Dynamik des Regelkreises mit steigender Totzeit ungünstig. Abhilfe bieten Regler mit Spezialstrukturen wie z. B. das Verfahren des Smith-Prädiktors.

Enthält die Regelstrecke neben PT1-Gliedern eine im Verhältnis zu einer dominanten Zeitkonstante $T$ eine nennenswerte Totzeit $T_{t}$ , ist ein I-Glied innerhalb des Regelkreises notwendig. Eine aus reiner Totzeit bestehende Regelstrecke kann – abgesehen von Spezialreglern – nur durch einen I-Regler geregelt werden.

Die Regelung einer Regelstrecke mit globaler Totzeit (keine weiteren Übertragungsglieder) mit einem I-Regler weist eine Besonderheit auf, dass die Kreisverstärkung

K={\frac {k_{1}}{T_{t}}}

; mit

k_{1}

= beliebig wählbarer Faktor, der das Einschwingverhalten der Regelgröße bestimmt.

Auch die Grenzstabilität (konstante Dauerschwingungen) eines solchen Regelkreises weist Regeln auf. Beispielsweise ergibt sich für $T_{t}=1$ [s] laut numerischer Berechnung eine Kreisverstärkung von K = 1,566, bei der die Regelgröße mit konstanter Amplitude schwingt. Beträgt die Totzeit $T_{t}=2$ [s], gilt für die Verdopplung der Totzeit der halbe Wert der Kreisverstärkung K = 0,783.

Bei festem Wert von $k_{1}$ ergibt sich für beliebige Werte $T_{t}$ die gleiche Höhe der Überschwingung ü. Ebenso ergibt sich in Abhängigkeit von der Kreisverstärkung $K$ und der Höhe der Überschwingung ü eine einfache Beziehung des ersten Nulldurchgangs der Sollregelgröße $y(t)$ . Diesen Zeitraum vom Zeitpunkt $t_{0}$ bis zum Erreichen des ersten Nulldurchgangs bezeichnet man als Anregelzeit:

T_{A}

= Verzugszeit

T_{u}

+ Anstiegszeit

T_{g}

.

Regelung einer Regelstrecke als reines Totzeitglied

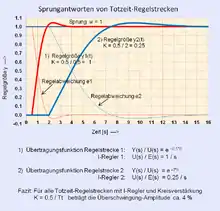
Sprungantworten eines Regelkreises mit 2 unterschiedlichen Totzeit-Regelstrecken

Mittels der numerischen Berechnung wurden folgende Zusammenhänge bei der Berechnung eines Regelkreises mit einer Regelstrecke $G_{s}(s)=e^{-T_{t}\cdot s}$ und einem Regler $G_{R}(s)={\frac {K}{s}}={\frac {k_{1}}{T_{t}\cdot s}}$ gefunden. Damit ist es möglich, für die Parametrierung eines Reglers bei gegebener Regelstrecke mit globaler Totzeit wichtige Parameter für einen stabilen Regelkreis und des Einschwingvorgangs zu finden.

Wählt man die Kreisverstärkung $K$ für einen festen Zahlenwert $k_{1}$ , beträgt die Überschwingung ü des Einschwingvorgangs der Regelgröße und die Anregelzeit $T_{A}$ für

$k_{1}=0{,}7\to {\text{ü}}\approx 20\,\%\quad \to T_{A}\approx 2{,}5\cdot T_{t}$
$k_{1}=0{,}6\to {\text{ü}}\approx 10\,\%\quad \to T_{A}\approx 3\cdot T_{t}$
$k_{1}=0{,}5\to {\text{ü}}\approx 4\,\%\quad \ \to T_{A}\approx 3{,}8\cdot T_{t}$

Beispiel einer gegebenen Regelstrecke mit globaler Totzeit:

Eingangssprung $e(t)=1(t)$

Regelstrecke gegeben: $G_{s}(s)=e^{-T_{t}\cdot s}$

für $T_{t}=0{,}5$ [s] und alternativ $T_{t}=2$ [s].

Geeigneter Regler: $G_{R}(s)={\frac {K}{s}}={\frac {0{,}5}{T_{t}\cdot s}}$ → für ü ≈ 4 %

Mit der Wahl von ü und $k_{1}$ lässt sich der Wert der Kreisverstärkung $K$ und der Wert der Anregelzeit $T_{A}$ ohne aufwendigere Simulation des Regelkreises errechnen. Siehe grafische Darstellung der Sprungantworten.

Regelstrecke mit Totzeit und weiteren PT1-Gliedern

In der Regelungstechnik ist die Parametrierung eines Reglers durch Kompensation der PT1-Verzögerungsglieder mit differenzierenden PD1-Gliedern üblich. Damit vereinfacht sich die Berechnung des aufgeschnittenen Regelkreises.

Es liegt nahe, die oben genannte Beziehung – Wahl der Kreisverstärkung für eine bestimmte Größe der Überschwingung ü – für Regelstrecken mit PT1- und Totzeit-Systemen zu nutzen, indem die PT1-Verzögerungszeiten durch PD1-Glieder des Reglers kompensiert werden.

Es wird darauf hingewiesen, dass es sich um ideale PD1-Glieder handelt, die sich technisch nicht herstellen lassen. Reale PD1-Glieder enthalten immer sogenannte parasitäre Verzögerungen, deren Zeitkonstanten in der Praxis etwa ein Zehntel der Zeitkonstanten der PD1-Glieder betragen.

Berechnungsbeispiel:

Regelstrecke gegeben:

G_{S}(s)={\frac {e^{-T_{t}\cdot s}}{(T_{1}\cdot s+1)(T_{2}\cdot s+1)}}

Diese Regelstrecke ist für einen PID-Regler geeignet, indem die beiden PD-Glieder des Reglers die beiden PT1-Glieder des Regelstreckenmodells kompensieren.

Der zugehörige passende ideale PID-Regler besteht aus zwei PD1-Gliedern und einem I-Glied:

G_{R}(s)={\frac {K\cdot (T_{v1}\cdot s+1)(T_{v2}\cdot s+1)}{s}}={\frac {0{,}6\cdot (T_{v1}\cdot s+1)(T_{v2}\cdot s+1)}{T_{t}\cdot s}}\quad {\text{für}}\ {\text{ü}}=10\,\%

Überschwingung.

Setzt man die Zahlenwerte für ein gewähltes ü ( $k1$ und $T_{t}$ ) ein und für die Zeitkonstanten $T_{v}=T$ , ergibt sich die Übertragungsfunktion des aufgeschnittenen Regelkreises zu:

G_{0}(s)={\frac {0{,}6\cdot e^{-T_{t}\cdot s}}{T_{t}\cdot s}}\quad {\text{für}}\ {\text{ü}}=10\,\%

Überschwingung.

Damit sind die Parameter des Reglers für die reale Regelstrecke wie folgt gegeben:

Kreisverstärkung

K={\tfrac {0{,}6}{T_{t}}}

für eine Überschwingung von ca. 10 %, Zeitkonstanten des Reglers

T_{v}=T

. Die Anregelzeit des geschlossenen Regelkreises beträgt

T_{A}\approx 3\cdot T_{t}

.

Möchte man den kontinuierlichen Verlauf der Sprungantwort der Regelgröße des geschlossenen Regelkreises berechnen, kann die oben stehende Übertragungsfunktion des aufgeschnittenen Regelkreises $G_{0}(s)$ mittels numerischer Berechnung benutzt werden, wenn die Schließbedingung für die Regelabweichung $e_{(k)}=w_{(k)}-y_{(k-1)}$ zusätzlich eingeführt und für die Integration die entsprechende Differenzengleichung eingesetzt wird. Für die Berechnung des Totzeitgliedes eignet sich am besten die INDEX-Funktion oder ein genaues Totzeit-Modell.

Einzelnachweise

Siehe Fachbuch: Lutz / Wendt: „Taschenbuch der Regelungstechnik mit MATLAB und Simulink; Kapitel: Totzeit-Element (PT_t-Element).“
Der Realteil der Laplace-Variable s wird in der Fachliteratur unterschiedlich bezeichnet: $\delta$ oder $\sigma$ , Fachbuchautor Prof. Dr.-Ing. Jan Lunze, Universität Bochum, bevorzugt $\delta$ .
Lutz / Wendt: Taschenbuch der Regelungstechnik, Kapitel: „Mathematische Methoden zur Berechnung von digitalen Regelkreisen im Zeitbereich, Unterkapitel: Differenzengleichungen“.
Siehe Vorlesungsskript Universität Siegen, Prof. Dr.-Ing Oliver Nelles: Mess- und Regelungstechnik I: „Allpässe und nicht phasenminimale Systeme“

Literatur

G. Schulz: Regelungstechnik 1: Lineare und Nichtlineare Regelung, Rechnergestützter Reglerentwurf. 3. Auflage. Oldenbourg, München 2007, ISBN 978-3-486-58317-5.
M. Reuter, S. Zacher: Regelungstechnik für Ingenieure: Analyse, Simulation und Entwurf von Regelkreisen. 12. Auflage. Vieweg+Teubner, 2008, ISBN 978-3-8348-0018-3.
J. Lunze: Regelungstechnik 1 – Systemtheoretische Grundlagen, Analyse und Entwurf einschleifiger Regelungen. Springer-Verlag, 2006, ISBN 3-540-28326-9.
H. Unbehauen: Regelungstechnik 1. Vieweg Verlag, 2007, ISBN 978-3-528-21332-9.
H. Lutz, W. Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink. 12. Auflage. Europa-Verlag, 2021, ISBN 978-3-8085-5870-6.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Siehe Fachbuch: Lutz / Wendt: „Taschenbuch der Regelungstechnik mit MATLAB und Simulink; Kapitel: Totzeit-Element (PT_t-Element).“

[2] Der Realteil der Laplace-Variable s wird in der Fachliteratur unterschiedlich bezeichnet: $\delta$ oder $\sigma$ , Fachbuchautor Prof. Dr.-Ing. Jan Lunze, Universität Bochum, bevorzugt $\delta$ .

[3] Lutz / Wendt: Taschenbuch der Regelungstechnik, Kapitel: „Mathematische Methoden zur Berechnung von digitalen Regelkreisen im Zeitbereich, Unterkapitel: Differenzengleichungen“.

[4] Siehe Vorlesungsskript Universität Siegen, Prof. Dr.-Ing Oliver Nelles: Mess- und Regelungstechnik I: „Allpässe und nicht phasenminimale Systeme“