Pol-Nullstellen-Diagramm

Das Pol-Nullstellen-Diagramm, kurz PN-Diagramm, stellt die Pole und Nullstellen der Übertragungsfunktion eines Systems in der komplexen Zahlenebene dar. Das System kann ein elektrisches System sein, z. B. ein Filter, es kann aber auch ein zu regelndes mechanisches System sein, z. B. ein Fahrzeug bei einer Fahrdynamikregelung. Am häufigsten angewendet werden Pol-Nullstellen-Diagramme in der Nachrichtentechnik und der Regelungstechnik.

Aus einem Pol-Nullstellen-Diagramm kann u. a. auf den Betrags- und Phasenverlauf des Frequenzgangs eines Systems sowie auf dessen Impuls- und Sprungantwort geschlossen werden. Damit bildet es eine wertvolle Grundlage für Analyse, Synthese und Stabilitätsbetrachtungen von Schaltungen, Filtern und anderen Übertragungssystemen.

Die Erstellung und Anwendung eines Pol-Nullstellen-Diagramms setzt entsprechende Kenntnisse der Mathematik und der Systemtheorie voraus. Bei der Übertragungsfunktion, deren Pole und Nullstellen dargestellt werden, handelt es sich um die Laplace-Transformierte der Impulsantwort oder die z-Transformation eines Systems.

Üblicherweise werden im PN-Diagramm markiert:

Einfachpole durch ein Kreuz
Mehrfachpole durch ein Doppelkreuz
Nullstellen durch einen kleinen Kreis.

Praktisch unterstützt wird die Erstellung von Pol-Nullstellen-Diagrammen oder die Herleitung von Übertragungsfunktionen oder anderen Systemeigenschaften aus Pol-Nullstellen-Diagrammen heute oft durch Software.

Bedeutung der Pol- und Nullstellenlagen

Aus der Lage der Pole kann man u. a. erkennen, ob ein System kausal und stabil ist. Pole bestimmen das Zeitverhalten des Systems.

Das System ist stabil, wenn alle Pole der Übertragungsfunktion in der offenen linken Halbebene (LHE) des Diagramms liegen. Besitzt ein Pol einen Realteil von 0, d. h. liegt er auf der (meist senkrecht gezeichneten) imaginären Achse, so ist das System grenzstabil.

Realisierbare (kausale) Systeme besitzen mindestens so viele Pole wie Nullstellen. Aus dem Abstand aller Pole- und Nullstellen zu einer Frequenz im Diagramm kann man die Frequenzübertragungseigenschaften abschätzen. Eigenschwingvorgänge werden durch zwei konjugiert-komplexe Pole aufgezeigt. Komplexe Pole in der offenen linken Halbebene deuten auf abklingende Schwingungen.

All diese anschaulichen Diagramminterpretationen und viele weitere Interpretationen dieser Art lassen sich mit der Systemtheorie der Nachrichtentechnik gewinnen.

Bewegt man sich auf der Frequenzachse von $-\infty$ nach $+\infty$ , so dreht jeder Pol in der LHE sowie jede Nullstelle in der rechten Halbebene (RHE) die Phase um $-{\frac {\pi }{2}}$ ; jede Nullstelle in der LHE bewirkt eine Phasendrehung um $+{\frac {\pi }{2}}$ .

Beispiel

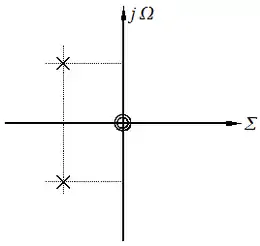
Im Folgenden sind die Systemfunktion, das Pol-Nullstellen-Diagramm und das Bode-Diagramm für einen Hochpass 2. Ordnung angegeben:

Übertragungsfunktion	PN-Schema	Bode-Diagramm
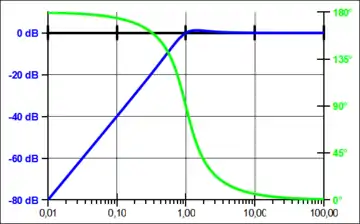$H(s)={\frac {\left({\frac {s}{\Omega _{z}}}\right)^{2}}{1+{\frac {s}{\Omega _{p}Q_{p}}}+\left({\frac {s}{\Omega _{p}}}\right)^{2}}}$ $\Omega _{z}=\Omega _{p}$

Wie zu sehen ist, besitzt ein Hochpass 2. Ordnung ein konjugiert komplexes Polstellenpaar und eine doppelte Nullstelle im Koordinatenursprung. Das System ist somit stabil.

Minimalphasige Systeme, zu denen auch dieses Beispiel gehört, haben keine Null- und Polstellen in der RHE.

Literatur

Otto Föllinger, Mathias Kluwe: Laplace-, Fourier- und z-Transformation. 10. Auflage. VDE Verlag, Berlin 2011, ISBN 978-3-8007-3257-9.
Dieter Kreß, Benno Kaufhold: Signale und Systeme verstehen und vertiefen. 1. Auflage. Vieweg + Teubner Verlag, Wiesbaden 2010, ISBN 978-3-8348-1019-9.
James G. Holbrook: Laplace-Transformation. Lehrbuch für Elektrotechniker und Physiker, 2. Auflage, Springer Fachmedien, Wiesbaden 1973, ISBN 3-663-01883-0.
Thomas Frey, Martin Bossert: Signal- und Systemtheorie. 1. Auflage. B. G. Teubner Verlag, Stuttgart 2004, ISBN 3-519-06193-7.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.