Moll

Moll (von lateinisch mollis ‚weich‘; französisch mode mineur, englisch minor, italienisch modo minore, spanisch modo menor) bezeichnet in der Musik ein Tongeschlecht. Dieses kann sich auf eine Tonart, eine Tonleiter oder einen Akkord beziehen. Moll bildet mit Dur ein Begriffspaar und teilt dessen Benennungs- und Bedeutungsgeschichte.

Dur Moll

Die Gesamtheit aller Dur- und Molltonarten nennt man auch Dur-Moll-System. Dieses löste im 17. und 18. Jahrhundert das System der Kirchentonarten ab.

Kennzeichnend für das Moll-Geschlecht ist das Intervall einer kleinen Terz zwischen Grundton und Terz des Tonmaterials. Die kleine Terz über dem Grundton wird deshalb auch Mollterz genannt.

Die Bemühung, die Namen von Dur und Moll auch im Schriftbild zu unterscheiden, hat zahlreiche Schreibvarianten hervorgebracht. Die heute bevorzugte Schreibweise ist C-Dur und c-Moll, jedoch sind auch noch diverse alternative Schreibweisen im Gebrauch. Siehe hierzu den Abschnitt Schreibweisen im Artikel Tonart.

Zur Etymologie siehe Dur: Etymologie.

Molltonleiter

Natürliches Moll

Die natürliche Molltonleiter oder reine Molltonleiter des „reinen“ bzw. „äolischen Molls“ oder „Naturmolls“ ist eine heptatonische Tonleiter mit Halbtonschritten zwischen der zweiten und dritten sowie der fünften und sechsten Stufe und Ganztonschritten zwischen den übrigen. Seit dem 16. Jahrhundert ist die Mollskala die nach der Durskala am zweithäufigsten verwendete Tonleiter der abendländischen Musik.

Die natürliche a-Moll-Tonleiter besteht ausschließlich aus Stammtönen: A, H, C, D, E, F, G, A.

Harmonisches Moll

a-Moll, d-Moll, E-Dur
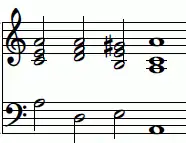
a-Moll-Kadenz mit Dominant-Dur-Dreiklang

Die Tonleiter des harmonischen Molls, die harmonische Molltonleiter, ist eine Variante der natürlichen Molltonleiter, bei der die siebte Stufe um einen Halbton erhöht ist. Dies geschieht, um die aus Dur bekannte Leittonwirkung auch in Moll zu erzielen. Der Dominantdreiklang wird dann zu einem Durdreiklang. Zum Beispiel wird die siebte Stufe g von a-natürlich-Moll zum Leitton gis erhöht.

Die harmonische Molltonleiter ist eine Zusammenstellung der Töne, die in einer kadenzierenden Akkordfolge mit einem Molldreiklang als Subdominante und einem Durdreiklang als Dominante vorkommen. Da hierbei der harmonische Aspekt im Vordergrund steht, erklärt sich der Name dieser Variante.

Zwischen sechster und siebter Stufe entsteht ein so genannter Hiatus-Schritt (drei Halbtöne). Der Hiatus, welcher der Skala einen orientalischen Anklang gibt, wurde in der abendländischen Musik aufgrund seiner Unsanglichkeit als melodischer Schritt weitgehend vermieden und findet sich allenfalls gelegentlich in der Instrumentalmusik.

Die Töne der harmonischen a-Moll-Tonleiter sind: A, H, C, D, E, F, Gis, A.

Melodisches Moll

Die harmonische Molltonleiter enthält den schwer singbaren Hiatus-Schritt zwischen sechster und siebter Stufe. Um ihn zu vermeiden, wird bei der melodischen Molltonleiter die sechste Stufe ebenfalls erhöht. Damit entspricht die Skala bis auf den dritten Ton (Mollterz zum Grundton) der Durskala.

Da der künstlich erzeugte Leitton beim Abwärtsgehen nicht nötig ist, wird dann – abgesehen vom melodischen Moll im Jazz[1] – das natürliche Moll verwendet.

Die Tonstufen der melodischen a-Moll-Tonleiter aufwärts sind: A, H, C, D, E, Fis, Gis, A.

Literaturbeispiel

Melodisches wie auch harmonisches Moll dienen häufig der Hervorhebung kurzer Passagen, meistens des Schlusses, wo ansonsten meist natürliches Moll erklingt. Das obige Beispiel zeigt dies: Nach zwölf Takten natürlichem Moll (ohne Versetzungszeichen) kommt erst im vorletzten Takt melodisches Moll, und der letzte Takt kann auch als harmonisches Moll interpretiert werden.

Für die Einbeziehung der Leiter in die Akkord-Skalen-Theorie ist jedoch die unterschiedliche Form je nach Aufwärts- oder Abwärtsbewegung der Leiter unbrauchbar. Man verwendet daher hier nur die Aufwärtsform und bezeichnet sie als „Melodisch Moll aufwärts“ (kurz „MMA“). Die MMA-Leiter ist Grundlage für viele im Jazz oft verwendete Tonleitern.

Zigeunermoll

Diese weitere Variante der Molltonleiter wird in der Zigeunermusik (insbesondere die Musik der Sinti und Roma), aber auch z. B. bei Franz Liszt (Ungarische Rhapsodien) verwendet. Sie entspricht dem harmonischen Moll mit erhöhter vierter Stufe. Dadurch entsteht ein zweiter übermäßiger Sekundschritt (Hiatus) zwischen der dritten und vierten Stufe, der – ähnlich wie beim harmonischen Moll – einen besonderen orientalischen Anklang erzeugt.

Die Töne der a-Zigeunermoll-Tonleiter sind: A, H, C, Dis, E, F, Gis, A.

Bildliche Darstellungen

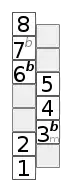Schematische Darstellung der reinen Molltonleiter
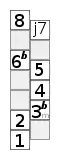Schematische Darstellung der harmonischen Molltonleiter
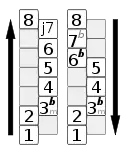Schematische Darstellung der melodischen Molltonleiter
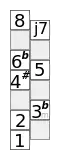Bildliche Darstellung der Zigeunermoll-Tonleiter

Beziehungen zu Dur

Durvariante

Die Varianttonart einer Molltonart hat denselben Grundton (beispielsweise a-Moll und A-Dur), besitzt jedoch aufgrund der bei Dur unterschiedlichen Stufenfolge andere Vorzeichen bzw. eine andere Vorzeichnung. Die Durvariante liegt im Quintenzirkel stets drei Schritte weiter in Kreuz-Richtung als die zugrundeliegende Molltonart, unterscheidet sich von dieser also immer um drei Vorzeichen. So wird z. B. e-Moll mit einem Kreuz, E-Dur aber mit vier Kreuzen vorgezeichnet.

Durparallele

Zu jeder Molltonart gibt es eine Paralleltonart in Dur, auch Durparallele genannt, die die gleichen Töne enthält und daher auch mit der gleichen Vorzeichnung notiert wird, jedoch eine kleine Terz höher beginnt (beispielsweise a-Moll – C-Dur).

Gegenklang

Der Gegenklang eines Mollakkords ist ebenfalls ein Durakkord, siehe auch Mediante.

Die unterschiedliche Wirkung von Dur und Moll

Von den meisten Menschen werden Dur und Moll in emotionaler Hinsicht unterschiedlich wahrgenommen. Neueren wissenschaftlichen Untersuchungen zufolge fehlt jedoch Kleinkindern die Fähigkeit einer solchen Unterscheidung und bildet sich erst ab einem Alter von ca. sechs Jahren heraus.[2]

Oft wird Dur mit „fröhlich“ und Moll mit „traurig“ in Verbindung gebracht. Diese Assoziationen sind aber fragwürdig, da sie zu der Annahme führen können, alle Lieder oder Musikstücke in Dur seien fröhlich, alle in Moll seien traurig. Dies ist jedoch falsch, denn der emotionale Charakter einer Musik wird unabhängig vom Tongeschlecht auch durch andere Komponenten wie Melodieführung, Rhythmus und Tempo bestimmt. So gibt es durchaus zahlreiche Moll-Lieder mit fröhlichem (Kalinka) und Dur-Lieder mit eher traurigem Charakter (Am Brunnen vor dem Tore).

Der Einfluss des Tongeschlechts auf den emotionalen Musikcharakter lässt sich folgendermaßen beschreiben: „Färbt“ man z. B. ein ohnehin trauriges Dur-Lied nach Moll um, so wirkt es danach noch trauriger, während ein bereits fröhliches Moll-Lied in der Dur-Version noch fröhlicher klingt. Das Tongeschlecht ist zwar nicht ausschlaggebend, bewirkt jedoch eine Verschiebung der Ausdrucksqualität in die eine oder andere Richtung.

Häufig begegnet man auch einer von emotionalen Aspekten unabhängigeren synästhetischen Charakterisierung von Dur und Moll durch Adjektive, die dem Bereich der visuellen Wahrnehmung entlehnt sind. So wird Dur gern als „hell“, „klar“ oder „strahlend“, Moll als „dunkel“, „düster“ oder „trübe“ beschrieben. Diese Charakterisierungen haben gegenüber den emotionalen Assoziationen mit „fröhlich“ und „traurig“ den Vorzug einer größeren Allgemeingültigkeit.

Ein akustischer Grund für die unterschiedliche Wirkung von Dur und Moll liegt darin, dass der Molldreiklang – verglichen mit dem Durdreiklang – einen geringeren Klangwert (Konsonanzgrad) hat. Dieser geringere „Wohlklang“ des Molldreiklangs ist z. B. dafür verantwortlich, dass dieser im Unterschied zum Durdreiklang lange Zeit nicht als schlussfähige Konsonanz angesehen wurde. Erst im Verlauf des Barockzeitalters verlor sich allmählich die bis dahin gängige Praxis, Musikstücke in Moll nicht mit einem Moll-, sondern einem Durdreiklang (vgl. Picardische Terz) enden zu lassen.

Für den erwähnten Klangwertunterschied zwischen Dur- und Molldreiklang werden mehrere voneinander unabhängige Gründe herangezogen:

In der Obertonreihe z. B. des (großen) C ist ein C-Dur-Dreiklang als vierter, fünfter und sechster Oberton enthalten: c’ – e’ – g’, wobei der Grundton als erster „Oberton“ mitgezählt wurde. Der c-Moll-Dreiklang kommt jedoch in der Obertonreihe des C nicht vor.
Die hierdurch bedingte unterschiedliche Klangqualität von Dur- und Molldreiklang lässt sich durch ein Experiment am Klavier verdeutlichen: Schlägt man mit der linken Hand ein C an und gleichzeitig mit der rechten Hand einen Durakkord bestehend aus c’, e’ und g’, so ergibt sich ein vollkommen konsonanter Klang. Ersetzt man jedoch hierbei den Dur- durch einen Molldreiklang (c’, es’, g’), so reibt sich die Mollterz es’ mit dem e’, das als 5. Oberton des Grundtons C mitschwingt, so dass man den Eindruck eines eher dissonanten Klangs gewinnt. Das Experiment funktioniert bei reiner Stimmung noch besser als bei gleichstufiger.
Zum Vergleich von Dur- und Molldreiklang kann man auch das Phänomen der Kombinationstöne heranziehen. Hier genügt bereits eine Betrachtung der Differenztöne 1. Ordnung, deren Frequenzen sich aus der Frequenzdifferenz der beteiligten Einzeltöne ergeben. Beim C-Dur-Dreiklang (c’ – e’ – g’) ergeben sich als Differenztöne aller enthaltenen Intervalle (Quint, große und kleine Terz): c, C und C, beim c-Moll-Dreiklang (c’ – es’ – g’) entsprechend: c, As₁ und Es. Die Kombinationstonverhältnisse sind also beim Mollakkord deutlich komplizierter und „belastender“ als beim Durakkord.

Keine Rolle spielen die oben beschriebenen akustischen Unterschiede in einer Theorie des Psychologen Norman Cook, der auf eine andere Weise die unterschiedliche Wirkung des Dur- und Molldreiklangs zu begründen versucht, indem er eine Verbindung zum urtümlichen, tierischen und menschlichen Lautgebaren konstruiert.[3]

Das „Mollproblem“

Während der Durdreiklang (Grundton, große Terz und reine Quinte) sich leicht aus der Obertonreihe ableiten lässt, sind entsprechende Versuche für den Molldreiklang nicht in gleichem Maße schlüssig, weshalb die Erklärung des Molldreiklangs sich zu einem echten Problem, nämlich dem so genannten „Mollproblem“ ausweitete.

Der Molldreiklang (oder -akkord) setzt sich aus dem Grundton, dem dritten und dem fünften Ton der Molltonleiter(n) zusammen. Werden diese Intervalle – unabhängig von der jeweiligen Stimmung – als harmonisch-rein aufgefasst (also Prime 1:1, kleine Terz 6:5 und Quinte 3:2), so ergibt sich – analog zum Durdreiklang 4:5:6 – das Schwingungsverhältnis 10:12:15.

{\frac {1}{1}}:{\frac {6}{5}}:{\frac {3}{2}}

auf einen Nenner gebracht =

{\frac {10}{10}}:{\frac {12}{10}}:{\frac {15}{10}}={\frac {10:12:15}{10}}\quad \ldots \quad 10\,:\,12\,:\,15

Damit hat der Mollakkord zwar ebenfalls eine Entsprechung in der Obertonreihe, doch ist diese im Gegensatz zum Durakkord in mehrfacher Hinsicht problematisch:

Zum einen wird dieser Molldreiklang durch dazwischenliegende Teiltöne (11, 13, 14) unterbrochen, wodurch ihm ein komplexeres Schwingungsverhältnis als dem Durdreiklang zukommt, und zum anderen hat diese sog. „monistische“ (d. h. aus der Obertonreihe abgeleitete) Deutung des Mollakkordes keinen eindeutigen Grundton, da der „Erzeugerton“ der Obertonreihe (hier: C) nicht mit der Prim des Dreiklangs (hier: e² in e-Moll) übereinstimmt. Nach der Funktionstheorie Hugo Riemanns handelt es sich bei diesem e-Moll-Akkord um einen sog. „Leittonwechselklang“, eine „Scheinkonsonanz“, die sich aus den zwei benachbarten Durakkorden (C-Dur 8:10:12 und G-Dur 12:15:18) zusammensetzt und damit einem bitonalen Konstrukt gleichkommt.[4] Dies erschien vielen namhaften Musiktheoretikern des 19. und frühen 20. Jahrhunderts (etwa Moritz Hauptmann,[5] Arthur von Oettingen,[6] Hugo Riemann[7] und Sigfrid Karg-Elert[8]) dem Mollgeschlecht nicht angemessen, da sich sowohl aus dem komplexeren Schwingungsverhältnis, als auch aus dem doppelten Grundton auf einen dissonanten Klang schließen lässt.

Laut Paul Hindemith und vielen Anderen entsteht der Mollakkord dagegen durch Tiefalteration („Trübung“) der großen Durterz, die er durch das Unvermögen des Hörers oder Instrumentalisten, bei gleitenden Tonhöhen (Glissando) zwischen Groß- und Kleinterz zu unterscheiden, legitimiert sah:

„Was ist aber der Molldreiklang wirklich? Ich halte ihn, einer auch nicht mehr ganz neuen Theorie folgend, für eine Trübung des Durdreiklangs. Da es nicht einmal möglich ist, kleine und große Terz einwandfrei gegeneinander abzugrenzen, glaube ich nicht an einen polaren Gegensatz der beiden Akkorde. Sie sind die hohe und tiefe, starke und schwache, helle und dunkle, eindringliche und matte Fassung ein und desselben Klanges.“

– Paul Hindemith: Unterweisung im Tonsatz. S. 101.[9]

Bei dieser „Trübungstheorie“ wird der Mollakkord allerdings zu einem künstlich erzeugten Variantklang degradiert, der mit seinem Schwingungsverhältnis 4:4⁴/₅:6 keine Entsprechung in der Naturtonreihe aufweist. Die kleine Terz 6:5 entsteht dabei durch einen chromatischen Halbtonschritt abwärts (e–es in C-Dur/c-Moll), dem so genannten kleinen Chroma 25:24:

{\frac {5}{4}}:{\frac {25}{24}}={\frac {6}{5}}

aus diesem ergibt sich auch das Verhältnis

{4}:({5}:{\tfrac {25}{24}}):6=4\,:\,4{\tfrac {4}{5}}\,:\,6

Gegen eine solche Auffassung sprach sich bereits Johann Wolfgang von Goethe aus.

Die aus heutiger Sicht fast schon esoterisch anmutende Deutung des Mollakkordes als „Unterklang“ mit dem Schwingungsverhältnis ${\displaystyle {\tfrac {1}{4\$ (für Quinte:Terz:Prime, also in umgekehrter Reihenfolge!) – jener von Hindemith verworfene „polare Gegensatz“ – bringt ebenfalls erhebliche Probleme mit sich. Nach dieser Lehre (dem so genannten „harmonischen Dualismus“), der zu Beginn des 20. Jahrhunderts nahezu ein allgemeingültiger Konsens der Musikwissenschaft war, ist der Bezugston eines Molldreiklangs nicht dessen Prime, sondern seine Quinte, ohne allerdings die entsprechenden Konsequenzen für den musikalischen Satz zu bedenken bzw. zu fordern (etwa die Verdopplung der Quinte statt der gängigen Prime). Ferner wird dem objektiv verifizierbaren physikalischen Phänomen der Obertonreihe eine hypothetische, mathematisch konstruierte, reziproke Untertonreihe als gleichwertig gegenübergestellt:[10]

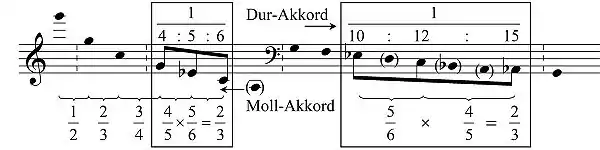
Aus diesem resultiert der Mollakkord als intervallgetreue, spiegelsymmetrische Umkehrung des Durdreiklangs, wobei sich die Durterz – mathematisch betrachtet – als arithmetisches Mittel von Prime a=1:1 und Quinte b=3:2 und umgekehrt die Mollterz als deren harmonisches Mittel erschließt; eine Betrachtungsweise, die bereits Gioseffo Zarlino in „Le Istituzioni harmoniche“ (1558) in ähnlicher Weise beschrieben hat:[11]

Das arithmetische Mittel

{\frac {1}{2}}\cdot (a+b)={\frac {1}{2}}\cdot \left({\frac {1}{1}}+{\frac {3}{2}}\right)={\frac {1}{2}}\cdot {\frac {2+3}{2}}={\frac {5}{4}}

.

Das harmonische Mittel

2:\left({\frac {1}{a}}+{\frac {1}{b}}\right)=2:\left({\frac {1}{1}}+{\frac {2}{3}}\right)=2:{\frac {5}{3}}={\frac {6}{5}}

.

Zwar stellt der „harmonische Dualismus“ damit die angestrebte Gleichberechtigung von Dur und Moll her, doch erschien vielen Kritikern diese Herleitung (insbesondere die Bezeichnung v. Oettingens, Riemanns und Karg-Elerts eines c-Moll-Dreiklangs als „Unter-g“ – mit der Chiffre °g, im Gegensatz zu c⁺ für C-Dur) nicht nur unnötig kompliziert:

„Aber so gelehrt bin ich schon lange nicht mehr angehaucht gewesen, dass ich mich für den Dualismus und die Bezeichnung des Moll-Akkordes entscheiden sollte.“

– Max Reger: Brief vom 13. November 1900 an Johannes Schreyer[12]

Dies war vielmehr auch praxisfern und mit den Ergebnissen der Musikpsychologie unvereinbar.

Trotz der unterschiedlichen Lehrmeinungen, wie das „Mollproblem“ zu lösen sei, bleibt die Intonation des Mollakkordes selbst bis hierhin unberührt und die Ergebnisse der einen Theorie lassen sich in die der anderen umrechnen, wobei aus (rein) mathematischer Sicht dem einfachsten Zahlenverhältnis der Vorzug gebührt:

„Nun ja --
Daß aber noch heute bei sehr vielen Theoretikern der Mollakk. als ein Durakk.(!) mit alterierter(!!) Terz gilt, ist eher zum Weinen als zum Lachen! Ein Handwerker weiß um sein Material besser Bescheid, als diese Leute, die sich schließlich noch für ‚Musikgelehrte‘ halten … Der Durakkord ist in S-Auffassung [Schwingungsverhältnis] der Komplex von 1 3 5, resp. in enger Grundstellung 4 : 5 : 6. Der Mollakkord ist in S-Auffassung entweder 4 : 4⁴/₅(!) : 6 oder 10 : 12 : 15. Im letzten Falle hätte er keine Prime, auf die sich die 12 (d. i. 6 od. 3) beziehen könnte. Nun ist 4 : 4⁴/₅ : 6 gleich ²⁰/₅ : ²⁴/₅ : ³⁰/₅, d.i. gekürzt 10 : 12 : 15, d.i. ferner auf Generalzähler 60 gebracht: ${\displaystyle {\tfrac {60\ 60\ 60}{6\$ gekürzt ${\overleftarrow {6:5:4}}$ !“

– Sigfrid Karg-Elert: Polaristische Klang- und Tonalitätslehre. S. 18

Einige Musiktheoretiker (etwa Otakar Hostinský[13] und Josef Achtélik[14]) versuchten dagegen die Schwächen der „monistischen“ Moll-Theorie durch zwar einfachere Zahlenproportionen des Mollakkordes auszugleichen, jedoch kann dies nur auf Kosten der harmonisch-reinen Intonation geschehen. Zur Diskussion stand etwa der Komplex aus 6., 7., und 9. Oberton, der scheinbar einem g-Moll-Dreiklang (g–b–d) entspricht. Hierbei wird allerdings aus der reinen Kleinterz 6:5 die so genannte „septimale Kleinterz“ 7:6, die mit ihren 266,87 Cent um einen Viertelton (ca. 48,77 Cent) zu klein erscheint. Ein solcher Dreiklang 6:7:9 kann bestenfalls als Teil des Septnonenakkordes 4:5:6:7:9, also eines dissonanten(!), dominantischen(!) Dur(!)-Akkords aufgefasst werden, zudem ergäbe sich als dessen Durparallele (b–d–f) das (unbrauchbare) Schwingungsverhältnis 7:9:10½ = 14:18:21 .

Noch problematischer ist der 11. Oberton, das sog. „Alphorn-fa“. Dieses liegt nun mit 551,318 Cent (für das Intervall 11:8) fast exakt zwischen den Tonstufen f (temperiert 500 Cent) und fis (600 Cent), und liefert damit „neutrale Terzen“ 11:9 (weder Dur noch Moll). Ein solcher neutraler Klang ergibt sich aus dem Schwingungsverhältnis 9:11:13½ = 18:22:27 (d–f/fis–a); beim 9., 11., und 15. Oberton (d–f/fis–h), einer Umkehrung des h-Moll-Akkordes, führt er dagegen zu einer verstimmten Wolfsquinte 22:15 (ca. 663 Cent) .

Das „Mollproblem“ bleibt damit zwar eines der ungelösten Schismen der Musiktheorie, doch hat es in der musikalischen Praxis kaum eine Bedeutung. Allerdings mag das Nebeneinander der drei verschiedenen Molltonleitern und die künstlich erhöhte Picardische Terz am Ende eines Musikstücks in der weniger stark ausgeprägten Grundton-Empfindung der Mollharmonik seinen Ursprung haben. Insbesondere die Komponisten der Romantik und Spätromantik, also eben die Komponisten jener Zeit, in der das Moll zu einem „Problem“ stilisiert wurde, sahen in der latenten Ambivalenz des Mollgeschlechts keinen Nach-, sondern im Gegenteil einen Vorteil. Die heute übliche Harmonielehre (etwa die Hermann Grabners[15] oder Wilhelm Malers[16]) kommt ihnen insofern entgegen, als dass sie sich des spekulativen Überbaus der Riemannschen Funktionstheorie sukzessive entledigte und sich mehr und mehr an den Verhältnissen der temperierten Stimmung orientiert.

Siehe auch

Literatur

Wieland Ziegenrücker: Allgemeine Musiklehre mit Fragen und Aufgaben zur Selbstkontrolle. Deutscher Verlag für Musik, Leipzig 1977; Taschenbuchausgabe: Wilhelm Goldmann Verlag, und Musikverlag B. Schott’s Söhne, Mainz 1979, ISBN 3-442-33003-3, S. 88–93.

Weblinks

Wiktionary: Moll – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Einzelnachweise

Dirk Bell: Jazz geht’s los. Teil III. In: Gitarre & Laute. 6, 1984, Heft 5, S. 54–56; hier: S. 54.
Für kleine Kinder klingt Musik in Moll nicht unbedingt traurig. Auf: wissenschaft.de vom 7. April 2001.
Manfred Dworschak: Täler des Wohlklangs. In: Der Spiegel. Nr. 32, 2008, S. 118–120 (online).
Rudolf Klein: Zur Definition der Bitonalität. In: Österreichische Musikzeitschrift. Band 6, 1951, S. 313; Klein, ein überzeugter „Monist“ spricht tatsächlich von der „Bitonalität des einfachen Mollakkords.“
Moritz Hauptmann: Die Natur der Harmonik und Metrik. Leipzig 1853.
Arthur von Oettingen: Harmoniesystem in dualer Entwicklung. Studien zur Theorie der Musik. Dorpat / Leipzig 1866; überarbeitete zweite Auflage als Das duale Harmoniesystem. Leipzig 1913.
Hugo Riemann: Das Problem des harmonischen Dualismus. Leipzig 1905.
Sigfrid Karg-Elert: Polaristische Klang- und Tonalitätslehre. Leipzig 1930.
Paul Hindemith: Unterweisung im Tonsatz. I. Theoretischer Teil. Mainz 1937.
Hugo Riemann: Die objective Existenz der Untertöne in der Schallwelle. Kassel 1875.
vgl.: Carl Dahlhaus: War Zarlino Dualist? In: Die Musikforschung. Band 10, 1957, S. 286ff.
Else Hase-Koehler (Hrsg.): Max Reger – Briefe eines deutschen Meisters – ein Lebensbild. 2. Auflage. Leipzig 1938, S. 81.
Otakar Hostinský: Die Lehre von den musikalischen Klängen. Prag 1879.
Josef Achtélik: Der Naturklang als Wurzel aller Harmonien. Eine aesthetische Musiktheorie in zwei Teilen. Leipzig 1922 und 1928.
Hermann Grabner: Handbuch der funktionellen Harmonielehre. Regensburg 1944.
Wilhelm Maler: Beitrag zur durmolltonalen Harmonielehre. München 1957.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Dirk Bell: Jazz geht’s los. Teil III. In: Gitarre & Laute. 6, 1984, Heft 5, S. 54–56; hier: S. 54.

[2] Für kleine Kinder klingt Musik in Moll nicht unbedingt traurig. Auf: wissenschaft.de vom 7. April 2001.

[3] Manfred Dworschak: Täler des Wohlklangs. In: Der Spiegel. Nr. 32, 2008, S. 118–120 (online).

[Bitonalität-4] Rudolf Klein: Zur Definition der Bitonalität. In: Österreichische Musikzeitschrift. Band 6, 1951, S. 313; Klein, ein überzeugter „Monist“ spricht tatsächlich von der „Bitonalität des einfachen Mollakkords.“

[Mauptmann-5] Moritz Hauptmann: Die Natur der Harmonik und Metrik. Leipzig 1853.

[Dualismus-6] Arthur von Oettingen: Harmoniesystem in dualer Entwicklung. Studien zur Theorie der Musik. Dorpat / Leipzig 1866; überarbeitete zweite Auflage als Das duale Harmoniesystem. Leipzig 1913.

[Riemann-7] Hugo Riemann: Das Problem des harmonischen Dualismus. Leipzig 1905.

[Sigfrid_Karg-Elert-8] Sigfrid Karg-Elert: Polaristische Klang- und Tonalitätslehre. Leipzig 1930.

[Hindemith-9] Paul Hindemith: Unterweisung im Tonsatz. I. Theoretischer Teil. Mainz 1937.

[Untertöne-10] Hugo Riemann: Die objective Existenz der Untertöne in der Schallwelle. Kassel 1875.

[Zarlino-11] vgl.: Carl Dahlhaus: War Zarlino Dualist? In: Die Musikforschung. Band 10, 1957, S. 286ff.

[Reger-12] Else Hase-Koehler (Hrsg.): Max Reger – Briefe eines deutschen Meisters – ein Lebensbild. 2. Auflage. Leipzig 1938, S. 81.

[Hostinský-13] Otakar Hostinský: Die Lehre von den musikalischen Klängen. Prag 1879.

[Achtélik-14] Josef Achtélik: Der Naturklang als Wurzel aller Harmonien. Eine aesthetische Musiktheorie in zwei Teilen. Leipzig 1922 und 1928.

[Grabner-15] Hermann Grabner: Handbuch der funktionellen Harmonielehre. Regensburg 1944.

[Maler-16] Wilhelm Maler: Beitrag zur durmolltonalen Harmonielehre. München 1957.