Funktionstheorie

Die Funktionstheorie ist Teilgebiet der Musiktheorie und gehört zur Harmonielehre. Sie beschreibt die Verhältnisse und Spannungen zwischen den Akkorden in dur-moll-tonaler Musik. Hugo Riemann erarbeitete sie 1893. Sie wurde vor allem durch Wilhelm Maler und Diether de la Motte ausgearbeitet und erweitert.

Nutzen

Die Funktionstheorie dient der Musikanalyse. Harmonische Abläufe können auf ihrer Grundlage bestimmt und beschrieben werden. Sie setzt dabei die Hörerwartung bestimmter Abfolgen von Harmonien voraus, zum Beispiel Kadenzen und Sequenzen. Ebenso kann mit ihrer Hilfe auch die Gliederung längerer Musikstücke betrachtet werden.

Die Funktionstheorie lässt sich vor allem auf die Harmonik der Musik des Barock, der Klassik, dem Großteil der Romantik, aber nur auf kleinere Teile der Musik der Moderne anwenden. Auch viele harmonische Beziehungen innerhalb der Jazz- und Popmusik lassen sich mit der Funktionstheorie erfassen. In der Jazztheorie herrscht allerdings die Analyse nach der Stufentheorie und der Akkordskalentheorie vor. In der populären Musikliteratur werden einzelne Begriffe der Funktionsanalyse und Stufentheorie oft synonym verwendet.

Beide Systeme sind legitime und meist einfach nachvollziehbare Modelle zur Beschreibung harmonischer Zusammenhänge. Vom Kontext hängt ab, welchem Verfahren der Vorzug gegeben wird. Allerdings ist die Wahl zwischen Stufen- oder Funktionstheorie auch stark ortsabhängig. So wird außerhalb von Deutschland größtenteils ausschließlich mit der Stufentheorie gearbeitet, während hauptsächlich exklusiv in Deutschland auch heute noch häufig die vielmals kritisierte Funktionstheorie zum Einsatz kommt.[1][2]

Die Funktionen

Hauptfunktionen

Die Hauptfunktionen als Akkorde der C-Dur-Tonleiter

Die Hauptfunktionen als Akkorde
der harmonischen a-Moll-Tonleiter

Die Parallelen als Akkorde der C-Dur-Tonleiter

Die Parallelen als Akkorde der reinen a-Moll-Tonleiter

In der Funktionstheorie gilt der Dreiklang auf der ersten Stufe einer Tonart, die sich in einem bestimmten Zeitabschnitt manifestiert, als die Tonika (in der Stufentheorie: 1. Stufe) dieses Abschnitts. Zu ihr gesellen sich zwei weitere Hauptfunktionen, und zwar die nächsten quintenreinen Verwandten: die Dominante (Oberquinte, 5. Stufe) und die Subdominante (Quarte bzw. Unterquinte, 4. Stufe). Die Funktionen selbst werden in der Funktionstheorie mit Buchstaben bezeichnet, wobei Dur-Funktionen Großbuchstaben und Moll-Funktionen Kleinbuchstaben erhalten.

Nebenfunktionen

Dazu kommen die Nebenfunktionen, die im Terzabstand zu den Hauptfunktionen stehen. Zur symbolischen Darstellung der Nebenfunktionen wird den Hauptfunktionen ein Buchstabe angehängt.

Die Nebenfunktionen umfassen mehrere Gruppen:

die Parallelen im Kleinterzabstand zur Hauptfunktion
Hauptfunktion in Dur: Parallelklang (in Moll) nach unten –Tp–, bzw.
Hauptfunktion in Moll: Parallelklang (in Dur) nach oben –tP–
die Gegenklänge im Großterzabstand
Hauptfunktion in Dur: Gegenklang (in Moll) nach oben –Tg–, bzw.
Hauptfunktion in Moll: Gegenklang (in Dur) nach unten –tG–
die Medianten im Groß- oder Kleinterzabstand nach oben oder nach unten, die nicht aus tonleitereigenen Tönen gebildet werden können und durch Verdurung oder Vermollung der Hauptfunktion oder der Nebenfunktion erreicht werden.

Beispiele für Parallelen: Tp in C-Dur ist a-Moll. tP in a-Moll ist C-Dur.
Beispiele für Gegenklänge: Tg in C-Dur ist e-Moll. tG in a-Moll ist F-Dur.
Eine Mediante wäre E-Dur in C-Dur: TG (die Nebenfunktion ist verdurt),
eine andere es-Moll in c-Moll: tp (Haupt- und Nebenfunktion sind vermollt).

Vermollungen und Verdurungen gibt es auch für jede Hauptfunktion. Sie werden immer durch Groß- oder Kleinschreibung angedeutet (die vermollte Subdominante in einem Dursystem wird beispielsweise mit s statt S bezeichnet).

Kadenzen, Schlüsse und Modulationen

Die Tonika wird durch Kadenzen gefestigt. Die einfachsten Kadenzen sind D-T (authentischer Schluss) und S-T (plagaler Schluss). Als Grundmodell für Kadenzen wird in der Regel die Vollkadenz T-S-D-T angenommen.

Einfache Vollkadenz in C-Dur
Klangbeispiel

Die gleiche Kadenz in A-Dur
Klangbeispiel

Findet in einer Werkpassage ein Übergang von einer Tonart zu einer anderen durch diatonische, chromatische oder enharmonische Modulation statt, gilt die neue Tonart bei der Analyse solange als unbestätigt, bis eine authentische oder seltener auch plagale Kadenz folgt. Kann ein Akkord nicht nur als Funktion der bisherigen, sondern auch als Hauptfunktion der neuen Tonart begriffen werden, spricht man von Hauptzwischenfunktionen. Zu diesen gehört insbesondere die Zwischendominante, die nur im Fall von diatonischen Modulationen überhaupt möglich wird.

Zusätze in Form von Zahlen

Alle Symbole können mit Zusätzen in Form von Zahlen und Buchstaben versehen werden. Hochgestellte Zahlzusätze hinter der Funktionsbezeichnung zeigen Zusatztöne an. Unter das Funktionssymbol geschriebene Zahlen bezeichnen den Basston des Akkords im intervallischen Verhältnis zum Grundton der jeweiligen Funktion. Dreiklänge in Grundstellung werden ohne Zusatz geschrieben.

Die häufigsten Zusätze:

Septakkord auf der Dominante (D⁷)

Die Dominante von B ist F. Ein Dominantseptakkord auf F ist ein Vierklang mit dem zusätzlichen Ton Es.

Die Dominante von G ist D. Ein Dominantseptakkord auf D ist ein Vierklang mit dem zusätzlichen Ton C.

Septakkorde existieren in der Grundstellung (zum Dreiklang tritt eine Septime) sowie in drei Umkehrungen: 1. Umkehrung = Quintsextstellung, 2. Umkehrung = Terzquartstellung, 3. Umkehrung = Sekundstellung. Die Benennungen zeigen an, in welchen Intervallen zum untersten Ton des Akkordes die beiden Töne stehen, die die Sekunddissonanz ergeben. Bei der Bezeichnung nach der Funktionstheorie dagegen wird die hochgestellte 7 beibehalten, und man bezeichnet stattdessen den Basston relativ zum Akkordgrundton. So wird für die 1. Umkehrung eine tiefgestellte 3 hinzugefügt, weil in ihr die Terz des Akkordes in Grundstellung im Bass steht, für die 2. Umkehrung eine tiefgestellte 5 (Quinte im Bass), für die 3. Umkehrung eine tiefgestellte 7 (Septime im Bass). Im letzten Fall wird die Septime nur unter dem Funktionssymbol notiert, da daraus bereits hervorgeht, dass es sich um einen Septakkord handelt.

Die Funktionstheorie kennt die Möglichkeit, dass einem Akkord eine zusätzliche Sexte hinzugefügt wird (sixte ajoutée). Dies wird bezeichnet, indem man 5 und 6 hochstellt. Dieser Akkord wird in der Funktionstheorie normalerweise als Subdominante bewertet. Nach der Stufentheorie handelt es sich um einen Septakkord der II. Stufe in Quintsextstellung.

Außerdem werden Vorhalte notiert. Die Quarte ersetzt die Terz des Dominantdreiklangs (= Quartvorhalt) und wird anschließend aufgelöst:

Das folgende Beispiel enthält zwar scheinbar die Funktionalprogression T – T₅ – D – T, der zweite Akkord wird jedoch als Quartsextvorhalt zur nachfolgenden, echten Dominante gedeutet, da er auch so aufgelöst wird:

(Dieser Vorhalt wird auch mit D^T-D bezeichnet.)

Bei einem Nonenvorhalt wird dem Grundakkord eine None hinzugefügt, deren Auflösung zur Oktave umgehend folgt:

Andere Zeichen und Symbole

Alterationen: Hoch- und Tiefalterationen werden durch die Symbole < und > gekennzeichnet. Eine Dominante mit hochalterierter Quinte etwa erhält das Symbol D^5<, in C-Dur: g-h-dis

Ellipsen: Tritt ein erwarteter Klang nicht ein, kann man diesen trotzdem zusätzlich vermerken, um zu bezeichnen, was an dieser Stelle erwartet wurde. Der erwartete Klang wird hierbei in eckige Klammern gesetzt (z. B. [T]).; Bezieht sich ein Klang oder eine Klangfolge in ihrer Funktion auf eine andere Tonika als die zuletzt manifestierte (z. B. auf die zukünftige bei einer Modulation), so stellt man die gesamte Folge ab einem sinnvollen Punkt bis zur Manifestierung der neuen Tonika in runde Klammern.

Zwischenfunktionen: Wenn vor einen Akkord dessen (meist nicht leitereigene) Dominante tritt, ohne dass eine nennenswerte Modulation (Verlassen der Haupttonart) stattfindet, spricht man von einer Zwischendominante. Sie muss in der Bezeichnung nicht auf die eigentliche Grundtonart bezogen werden, sondern bezieht sich nur auf den ihr folgenden Akkord und hat das in Klammern eingeschlossene Funktionssymbol (D). Ebenso möglich, aber seltener sind Zwischensubdominanten mit dem Funktionssymbol (S).

Ligaturen: Ligaturen werden durch direkt an ein Funktionssymbol anschließende waagerechte Striche kenntlich gemacht und ziehen sich über mehrere Akkorde hin. Mit ihnen wird angezeigt, dass die beschriebene Funktion auch trotz eventueller fremder Töne über die Dauer der Ligatur (Bindung) als unverändert aufgefasst wird. Üblich ist dies z. B. bei Durchgängen. Über Ligaturen können ebenfalls Funktionssymbole stehen, die sich dann auf diejenige Funktion beziehen, bei der die Ligatur angesetzt hat.

Doppelfunktionen: Doppelfunktionen werden durch zwei ineinander verschränkte Funktionssymbole bezeichnet. Beispielsweise bezeichnet DD die Dominante der Dominante (Doppeldominante), SS die Subdominante der Subdominante (Doppelsubdominante).

Durchstreichungen: Durchstreichungen des Akkordsymbols, die nur bei Septakkorden eingesetzt werden, zeigen an, dass der Klang verkürzt ist, das heißt, ihm fehlt der Grundton. Hierdurch entsteht bei der Dominante ein verminderter Akkord, der in der Stufentheorie als Dreiklang auf der 7. Stufe gedeutet wird.

Spezielle Akkorde: Einige geläufigere Akkorde wie der neapolitanische Sextakkord, der verselbständigte neapolitanische Sextakkord, oder der verminderte Septakkord erhalten hochgestellte kleine Buchstaben:

sⁿ: Der neapolitanische Sextakkord (auch kurz Neapolitaner) wird entweder von der ersten Umkehrung des Dur-Akkordes auf der tiefalterierten zweiten Skalenstufe, oder alternativ von der Moll-Subdominante mit kleiner, skalenfremder Sexte (also quasi s^6>) abgeleitet. Beispiel für C-Dur: f-as-des.

S^N: Der verselbständigte Neapolitanische Sextakkord (auch kurz verselbständigter Neapolitaner) ist ein quasi in Grundstellung, also entgegen dem Namen nicht in Sextakkordstellung auftretender neapolitanischer Sextakkord. Beispiel für C-Dur: des-f-as.

D^v: Tritt der verminderte Septakkord (in C-dur: h-d-f-as) dominantisch in Erscheinung, wird er als verkürzter Dominantseptnonakkord gedeutet, dessen Funktionsbezeichnung eigentlich

{\cancel {D}}^{\begin{smallmatrix}9&>\\7&~\end{smallmatrix}}

, ein durchgestrichenes D mit hochgestellter 7 und 9>, wäre. Als vereinfachte Schreibweise verwendet man häufig D^v. Ist sein Auftreten dagegen eher subdominantisch, betrachtet die Funktionslehre ihn als Mollsubdominante mit Sixte ajoutée und Quarte statt Quinte, also als

s^{\begin{smallmatrix}6\\4\\3\end{smallmatrix}}

mit hochgestellter 3,4 und 6. Der Zwitterstatus dieses Akkordes drückt sich auch im Symbol der ineinander verschränkten Buchstaben D und s aus.

Funktionsharmonische Analyse eines Bach-Chorals

Beispiel einer funktionalen Analyse

Obwohl Bach die Funktionstheorie nicht bekannt war, lassen sich seine Choräle (in Grenzen) mit ihr beschreiben. Die folgende Analyse erhebt (natürlich) keinen Anspruch auf Vollständigkeit und Richtigkeit. Sie ist ebenso nur eine Interpretation des Chorals, andere sind durchaus denkbar. Gut zu sehen ist, dass die Komposition wegen der vielen kleinen Bewegungen in den einzelnen Stimmen nur sehr kompliziert vertikal, also harmonisch, beschrieben werden kann, was auf eine starke lineare Komponente zurückzuführen ist. Die Funktionstheorie wird dieser Musik eigentlich nicht gerecht, da harmonische Strukturen zu dieser Zeit vom Generalbass her gedacht wurden. Dennoch: die funktionsharmonische Analyse ist gängige Praxis, auch wenn sie schnell an ihre Grenzen in Bezug auf Übersichtlichkeit und Vollständigkeit stößt.

Klangbeispiel des analysierten Chorals (Midi)

Die vorliegende Analyse ist allerdings zwecklos, wenn sie nicht interpretiert wird. Im Grunde ist die Übersetzung in Funktionssymbole lediglich eine verallgemeinernde Betrachtung des komponierten Spezialfalls.

Ein Ansatzpunkt der Interpretation wäre zum Beispiel die Beschreibung der harmonischen Dramaturgie: Der erste Teil (bis zum Wiederholungszeichen) moduliert zur Dominante, was als bekanntes Prinzip der Sonata bzw. später der Sonatenhauptsatzform zu deuten wäre. Nachdem die Tonika zu Beginn des zweiten Teils zunächst gefestigt wurde (die Subdominante hat hier entscheidenden Anteil), entfernt sich der Satz sehr weit von ihr, die beiden verkürzten Zwischendominanten bieten im gleichen Zug eine neue Klangqualität. Nach der längsten Zäsur auf der erreichten Subdominantparallele etabliert sich wieder die Tonika, auffällig ist auch, dass die harmonische Bewegung zum Ende hin ruhiger wird, und das vollständige Fehlen von Zwischendominanten glättet den abschließenden Weg zum Grundklang. Besonders hervorzuheben wäre hier am Ende die zweimalige Schlusswendung T-S-D-T, sowie die Betonung (durch starke zeitliche Ausdehnung) der Dominante als vorletztem Klang.

Ein weiterer, möglicher Betrachtungsgegenstand wäre die Behandlung von Umkehrungen, im Besonderen die Stimmführung des Basses: Septimen werden ausnahmslos mit einem Sekundschritt nach unten fortgeführt, Terzen haben ebenfalls eine schrittige Umgebung usw.

Einschränkung

Nicht alle harmonischen Verwandtschaften und Fortschreitungen lassen sich mit Hilfe der Funktionstheorie fassen. Funktionsharmonik greift nur dort, wo es sich um mindestens in Dreiklangsharmonien konzipierte Musik handelt, der eine zentrale Dur- oder Molltonart zugrunde liegt. Daher ist die Funktionstheorie als Instrument der Analyse in dem Maße ungeeignet, wie die Musik diesen Bedingungen nicht entspricht.

So ist im Besonderen ein Großteil der Kunstmusik des 20. und 21. Jahrhundert, sowie die Musik der Renaissance mit Mitteln der Funktionstheorie häufig nicht zufriedenstellend, bis nahezu unmöglich zu erfassen. Erstere, da ein Großteil der Kunstmusik der Moderne auf nicht traditionellen Kompositionstechniken, wie der Polytonalität und Atonalität beruht. Letztere, da die Musik der Renaissance (welche zum Großteil polyphonische Vokalmusik ist) viel mehr horizontal als vertikal - sowohl gedacht, als auch musikalisch umgesetzt wurde. Natürlich bilden sich auch in der Musik der Renaissance Harmonien, aber aufgrund der speziellen Musikarchitektonik, die aber nicht nur aufgrund der horizontalen Ausrichtung Probleme bereiten kann, sondern ebenfalls aufgrund der zumeist polyphonen, komplizieren Melodik, welche die Funktionstheorie hier nicht als Mittel der Wahl erscheinen lassen.

Genauso ist die Funktionstheorie bei bestimmten harmonischen Verläufen, wie bspw. Quintfallsequenzen (besonders häufig im Barock) oder Akkorden, die auf nicht diatonischen Skalenstufen fußen (wie besonders häufig in Pop, Jazz oder Filmmusik eingesetzt, etwa bei der Tritonussubstitution oder Modal Interchange), eher schwierig einsetzbar. Bei diesen harmonischen Vorgängen greift die der Funktionstheorie gegenüberstehende Stufentheorie oft deutlich besser, da diese wesentlich rudimentärer und elementarer aufgebaut ist. In der Filmmusik ist beispielsweise, neben chromatischen Medianten, Modal Interchange und anderen harmonischen Spezifika, ein Wechsel zwischen Tonika und einem Durakkord auf der hochalterierten #IV, bzw. tiefalterierten bV Skalenstufe (einen Tritonus entfernt) gängige Praxis. Ginge man von C-Dur als Tonart und somit als Tonika aus, so wäre mit der Stufentheorie der Akkordwechsel zur #IV Skalenstufe sehr simpel als 'I - #IV' klassifizierbar (oder enharmonisch verwechselt als 'I - bV'); mit der Funktionstheorie dagegen aber fast unmöglich zu erfassen, außer man erweitert die Definitionen und führt neue Termini ein wie T' als Tritonustonart.

Der Wechsel von C nach Ges lässt sich durch die Theorie von der Gleichsetzung von Akkorden einfach erklären: Setzt man die Tonika C gleich mit der Dominante C (also der 5. Stufe in F-Dur), so kann man den Ges-Akkord als Umkehrung des neapolitanischen Sextakkordes in F-Dur interpretieren: eigentlich ein b-moll-Akkord ohne Quinte und mit tiefalterierter Sexte (Töne b - des - ges). Dieser Akkord sieht dann in der Umkehrung aus wie Ges-Dur. Dies wäre vor allem in Betracht zu ziehen als eine Möglichkeit zur Rückmodulation in die Tonika.

Spielt man die Akkordfolge C - Ges - F, wäre eine naheliegende Möglichkeit, dass man das F als neue Tonika hört (C = Dominante, Ges = Neapolitanischer Sextakkord, F = Tonika). Spielt man den F-Akkord nicht, wird kein kadenzielles Muster gespielt und somit auch kein nach der traditionellen Harmonielehre korrektes Ziel erreicht.

Auch die vorbarocke und spätmittelalterliche Musik (Ars nova) funktioniert eher nach melodischen bzw. kontrapunktischen Gesetzmäßigkeiten. Der harmonische Verlauf ergibt sich aus den Regeln des Fortschreitens innerhalb einer Stimme und des Verhältnisses jeweils zweier Stimmen zueinander, nicht durch eine übergeordnete harmonische Struktur. Die daraus entstehende Abfolge von Zusammenklängen ist allerdings der Ursprung unseres sich später entwickelnden Harmonieempfindens.

Im Blues sind Dominantseptakkorde Ruheklänge, so dass man von ${T}^{\begin{smallmatrix}7&~\end{smallmatrix}}$ und ${S}^{\begin{smallmatrix}7&~\end{smallmatrix}}$ statt Zwischenfunktionen ausgehen kann.

Jazz-Funktionsharmonik

Während die europäische traditionelle Musiklehre auf Dreiklängen basiert, sieht man im Jazz Vierklänge (drei Terzen übereinander) als Grundakkorde an. Die Stufenbezifferung besteht darin, dass man bei Dur-Akkorden die Bezifferung groß, bei Moll-Akkorden aber kleinschreibt. Zum Beispiel ionisch: I ii iii IV V vi vii oder dorisch: i ii III IV v vi VII.
Baut man auf den einzelnen Stufen einer beliebigen Tonleiter Akkorde auf, die nur aus Tönen dieser Skala bestehen, erhält man eine diatonische Reihe. Demnach besitzt jeder Modus neben dem horizontalen (melodischen) Aspekt auch einen vertikalen (harmonischen) Aspekt und somit auch eine leitereigene Harmonik. Dur und Moll sind nur ein Teil der Klangfarben, die theoretisch möglich sind.
Die nachfolgende Funktionstabelle zeigt die leitereigene Harmonik, wobei Funktionskürzel für Dur- und Moll-Stufen zusätzlich zur Groß-/Kleinschreibung entsprechend gefärbt sind.

Vertikale Sicht:

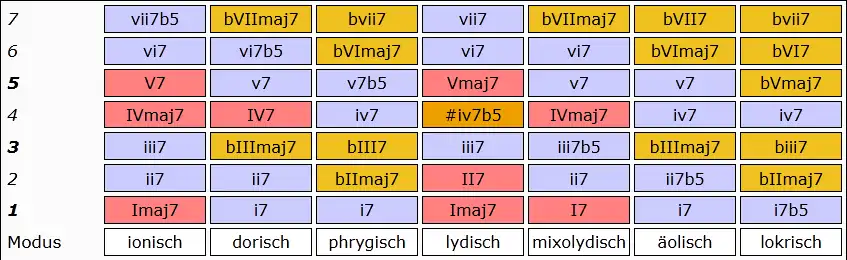
Ein »b« oder »#« wird immer dann vorangestellt, wenn eine Abweichung von der ionischen Skala vorliegt und zwar in Bezug auf Stufe und Tongeschlecht.

Siehe auch

Literatur

Wolf Burbat: Die Harmonik des Jazz. 5. Auflage. Deutscher Taschenbuch Verlag u. a., München u. a. 1998, ISBN 3-423-30140-6.
Hermann Grabner: Handbuch der funktionellen Harmonielehre (= Hesses Handbücher der Musik. 15 und 25, ZDB-ID 777229-4). 2 Bände (Bd. 1: Lehrbuch. Bd. 2: Aufgabenbuch.). Hesse, Berlin-Halensee u. a. 1944.
Richard Graf, Barrie Nettles: Die Akkord-Skalen-Theorie & Jazz-Harmonik. Advance Music, Rottenburg/N. 1997, ISBN 3-89221-055-1.
Hanno Hussong: Untersuchungen zu praktischen Harmonielehren seit 1945. dissertation.de, Berlin 2005, ISBN 3-89825-931-5 (Zugleich: Saarbrücken, Universität, Dissertation, 2004).
Wilhelm Maler: Beitrag zur durmolltonalen Harmonielehre. Band 1: Lehrbuch. 13. Auflage. Leuckart, München u. a. 1984, ISBN 3-920587-00-6.
Diether de la Motte: Harmonielehre (= dtv 30166). Gemeinschaftliche Original-Ausgabe, 13. Auflage. Deutscher Taschenbuch-Verlag u. a., München u. a. 2004, ISBN 3-423-30166-X.
Benedikt Stegemann: Theorie der Tonalität (= Taschenbücher zur Musikwissenschaft. 162). Noetzel, Wilhelmshaven 2013, ISBN 978-3-7959-0962-8.
Erich Wolf: Die Musikausbildung. Band 2: Harmonielehre. Akkordlehre, harmonische Funktionen, Modulationen, Harmonisierungstechnik, musikalischer Satz, Harmonieanalysen, Übungen. 6. Auflage. Breitkopf & Härtel, Wiesbaden 1992, ISBN 3-7651-0061-7.

Weblinks

Online-Tutorial zum Thema: Funktionstheorie und Sequenzen auf musikanalyse.net

Einzelnachweise

Lektoren-Vereinigung Korea: Peter Gahn - Fachsprache Musik als Vorbereitung für ein Musikstudium in Deutschland". In: lvk-info.org. Abgerufen am 26. März 2016.
ZGMTH - Von der Musiktheorie zum Tonsatz. In: www.gmth.de. Abgerufen am 26. März 2016.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Lektoren-Vereinigung Korea: Peter Gahn - Fachsprache Musik als Vorbereitung für ein Musikstudium in Deutschland". In: lvk-info.org. Abgerufen am 26. März 2016.

[2] ZGMTH - Von der Musiktheorie zum Tonsatz. In: www.gmth.de. Abgerufen am 26. März 2016.