Gegenklang
Gegenklänge, auch Gegenparallelen[1] oder Leittonwechselklänge bezeichnen Begriffe aus der Funktionstheorie und zählen zu den Nebenfunktionen einer Tonart. Sie sind mit den Hauptfunktionen (Tonika, Dominante und Subdominante) einer Tonart großterzverwandt und stellen quasi „Gegenpole“ zu den kleinterzverwandten Parallelklängen dar. In Dur liegen sie eine große Terz über, in Moll eine große Terz unter der zugehörigen Hauptfunktion. Gegen(drei)klänge[2] in Dur sind Molldreiklänge, in Moll sind es Durdreiklänge. In der Funktionstheorie werden sie durch ein an das Symbol der zugehörigen Hauptfunktion angehängtes g oder G gekennzeichnet, wobei Großbuchstaben für Dur, Kleinbuchstaben für Moll stehen.
| Bezeichnung | Dur (Beispiele in C-Dur) | Moll (Beispiele in a-Moll) |
|---|---|---|
| Tonikagegenklang | Tg auf der III. Stufe Bsp.: e-g-h | tG auf der VI. Stufe Bsp.: F-A-c |
| Dominantgegenklang | Dg auf der VII. Stufe Bsp.: H-d-fis (nicht leitereigen!) | dG auf der III. Stufe Bsp.: c-e-g |
| Subdominantgegenklang | Sg auf der VI. Stufe Bsp.: A-c-e | sG auf der erniedrigten II. Stufe Bsp.: B-d-f (nicht leitereigen!) |

Der Dominantgegenklang kommt als leitereigener Akkord auf der VII. Stufe der lydischen Tonleiter vor. In Dur kann er nicht ausschließlich aus leitereigenen Tönen gebildet werden, sondern nur, wenn man die IV. Stufe zur lydischen Quart erhöht. Entsprechend lässt sich der auf der II. Stufe von Phrygisch leitereigene Subdominantgegenklang in Moll nur darstellen, wenn man die II. Stufe zur phrygischen Sekunde erniedrigt. Der Gegenklang der Mollsubdominante tritt meist als Neapolitanischer Sextakkord, seltener auch als grundstelliger „verselbstständigter Neapolitaner“ in Erscheinung.
Leittonwechselklang

Die Bezeichnungen Gegenklang (Wilhelm Maler) und Gegenparallele (Hugo Distler) haben sich heute weitgehend gegenüber der ursprünglichen Bezeichnung von Hugo Riemann durchgesetzt, der solche Klänge Leittonwechselklang nannte. Ein solcher entsteht aus einem Dur-Dreiklang, wenn man dessen untersten Ton gegen den unter ihm liegenden Leitton auswechselt, wobei das Geschlecht von Dur nach Moll wechselt (im nebenstehenden Beispiel also e-Moll statt C-Dur). Aus einem Moll-Dreiklang wird ein Leittonwechselklang, wenn man seinen obersten Ton durch den über ihm liegenden (abwärtsführenden) Leitton ersetzt, wobei das Geschlecht von Moll nach Dur wechselt (im Beispiel F-Dur statt a-Moll).
Nach Riemanns eigener Formulierung entsteht ein Leittonwechselklang „durch Einstellung des Leittons zur Prim statt der Prim“.[3] Diese höchst einfache und allgemeine Definition ist nur möglich und verständlich vor dem Hintergrund, dass Riemann als Anhänger des harmonischen Dualismus im Molldreiklang ein Spiegelbild des Durdreiklangs sah: den Durdreiklang bezeichnete er als „Oberklang“, der aus Prim, großer Oberterz und Oberquint besteht, wogegen er den Molldreiklang als „Unterklang“ betrachtete, der aus Prim, großer Unterterz und Unterquint gebildet wird. Im Unterschied zur heutigen Auffassung ist also für Riemann die „Prim“ des Molldreiklangs nicht der unterste, sondern der oberste Ton. Entsprechend ist beim Durdreiklang der „Leitton zur Prim“ die kleine Untersekunde des untersten, beim Molldreiklang die kleine Obersekunde des obersten Tons.
Das folgende Notenbeispiel aus Riemanns Handbuch der Harmonielehre zeigt einige Beispiele für Leittonwechselklänge mit der von der heutigen Bezeichnungsweise stark abweichenden Riemannschen Funktionssymbolik:
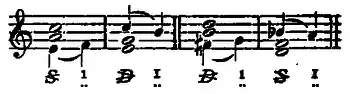
Riemann bezeichnet die Leittonwechselklänge durch Verschränkung der Symbole für die jeweiligen Hauptfunktionen (T,D und S) mit den Zeichen < und >, wobei < einen aufwärtsführenden und > einen abwärtsführenden Leitton bedeutet. Im Notenbeispiel lösen sich die Leittöne in die Prim der Ausgangsdreiklänge auf, wobei die „liegenden“ Doppelpunkte den darüber bezifferten Ton als Auflösungsziel kennzeichnen, während die arabische Ziffer 1 für die (unten liegende) Prim eines Durdreiklangs und die römische Ziffer I für die (oben liegende) Prim eines Molldreiklangs steht.
Obwohl die Leittonwechselklänge nur aus konsonanten Intervallen bestehen und satztechnisch als vollwertige Akkorde behandelt werden können, erscheinen sie wegen der enthaltenen Leittöne in bestimmten Zusammenhängen als auflösungsbedürftig und damit „auffassungsdissonant“. Riemann nennt sie „scheinkonsonant“ und benutzt gelegentlich auch den Terminus „Scheinharmonie“.
Verhältnis und Verwendung von Gegen- und Parallelklängen
Mit Ausnahme der Gegenklänge mit leiterfremden Tönen (Dominantgegenklang in Dur, Subdominantgegenklang in Moll) gibt es zu jedem Gegenklang einen zu einer anderen Funktion gehörenden Parallelklang, der mit ihm übereinstimmt. Die Beziehungen zwischen Gegen- und Parallelklängen im Einzelnen zeigt die folgende Tabelle:
| Funktion | in Dur (Bsp. in C-Dur) | in Dur identisch mit: | in Moll (Bsp. in a-Moll) | in Moll identisch mit: |
|---|---|---|---|---|
| Tonikagegenklang | Tg (e-g-h) / III. Stufe | Dominantparallele Dp | tG (F-A-c) / VI. Stufe | Subdominantparallele sP |
| Dominantgegenklang | Dg (H-d-fis) / VII. Stufe | dG (c-e-g) / III. Stufe | Tonikaparallele tP | |
| Subdominantgegenklang | Sg (A-c-e) / VI. Stufe | Tonikaparallele Tp | sG (B-d-f) / ♭II. Stufe |
Ob ein Akkord im konkreten Einzelfall als Gegen- oder Parallelklang zu deuten ist, hängt entscheidend davon ab, welche Hauptfunktion er im jeweiligen Kadenzverlauf stellvertretend verkörpert. Allgemein lässt sich sagen, dass der Tonikagegenklang Tg/tG von den Gegenklängen die häufigste Verwendung findet. Ansonsten bestehen zwischen Dur und Moll erhebliche Unterschiede, sodass eine getrennte Behandlung sinnvoll ist.
Verwendung in Dur

In Dur tritt die VI. Stufe fast ausschließlich als Tonikaparallele auf, insbesondere vertritt sie die Tonika bei Trugschlusswendungen. Die Verwendung als Subdominantgegenklang ist äußerst selten, aber immerhin möglich, wie das nebenstehende Kadenzbeispiel zeigt.
Die III. Stufe fungiert in den meisten Fällen als Tonikagegenklang, also als Stellvertreter der Tonika. Ihre Verwendung in dominantischer Funktion als Dominantparallele ist möglich (siehe nebenstehendes Beispiel), kommt aber selten vor. Die nahezu „exotische“ Schlusswendung Dp-T kann aber auch einen besonderen Reiz haben, wie die Schlusskadenz der Bilder einer Ausstellung beweist.
Der Dominantgegenklang wird nur äußerst selten verwendet.
Verwendung in Moll
In Moll fungiert die VI. Stufe hauptsächlich als Tonikagegenklang. Dieser spielt in Moll kadenziell eine ähnliche Rolle wie in Dur die Tonikaparallele, ist also z. B. auch Zielakkord bei Trugschlüssen. Die Verwendung als Subdominantparallele ist selten.
Die III. Stufe tritt praktisch nur als Tonikaparallele auf; als Vertreter der Dominante (dG) ist sie wegen des fehlenden Leitton ungeeignet.[4]
Der Subdominantgegenklang wird gerne als Neapolitaner verwendet.
Literatur
- Christoph Hempel: Neue allgemeine Musiklehre. 6. Auflage. Schott, Mainz 2008, ISBN 978-3-254-08200-8.
- Thomas Krämer: Harmonielehre im Selbststudium. 5. Auflage. Breitkopf & Härtel, Wiesbaden 2009, ISBN 978-3-7651-0261-5.
- Diether de la Motte: Harmonielehre. 16. Auflage. Bärenreiter, Kassel 2011, ISBN 978-3-7618-2115-2.
- Leittonwechselklang. In: Marc Honegger, Günther Massenkeil (Hrsg.): Das große Lexikon der Musik. Band 5: Köth – Mystischer Akkord. Aktualisierte Sonderausgabe. Herder, Freiburg im Breisgau u. a. 1987, ISBN 3-451-20948-9, S. 93.
- Leittonwechselklang. In: Wilibald Gurlitt, Hans Heinrich Eggebrecht (Hrsg.): Riemann Musiklexikon. 12. Auflage. Sachteil. B. Schott’s Söhne, Mainz 1967, S. 514.
- Reinhard Amon: Lexikon der Harmonielehre. 2. Auflage. Doblinger, Wien 2015, ISBN 978-3-902667-56-4.
Weblinks
- Everard Sigal: Tonsatz: leitereigene Dreiklänge. Abgerufen: 17. März 2012.
Anmerkungen und Einzelnachweise
- Eigentlich Gegenparallelklang, die Kurzform Gegenparallele hat sich jedoch allgemein durchgesetzt. Vgl.: Everard Sigal: Terzverwandtschaft. Abgerufen am 17. September 2015.
- Gegenklänge treten meist als Dreiklänge in Erscheinung, können aber theoretisch und in praktischen Einzelfällen auch mehr als drei Töne enthalten.
- Hugo Riemann: Handbuch der Harmonielehre. 1920, S. 80 ff. Abgerufen: 19. September 2015.
- Reinhard Amon: Lexikon der Harmonielehre. 2. Auflage. Doblinger, Wien 2015, ISBN 978-3-902667-56-4, S. 210.