Lineare Funktion

Als lineare Funktion wird oft (insbesondere in der Schulmathematik) eine Funktion ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} }$ der Form

${\displaystyle f(x)=m\cdot x+n;\quad m,n\in \mathbb {R} ,}$

also e​ine Polynomfunktion höchstens ersten Grades, bezeichnet.

Es handelt sich dabei jedoch nicht um eine lineare Abbildung im Sinne der linearen Algebra, sondern um eine affine Abbildung, da die Linearitätsbedingung im Allgemeinen nicht erfüllt ist. Man spricht deswegen auch von einer affin-linearen Funktion. Um eine lineare Abbildung bzw. lineare Funktion im Sinne der linearen Algebra handelt es sich nur im Spezialfall ${\displaystyle n=0}$, also ${\displaystyle f(x)=mx.}$ Solche Funktionen werden auch als homogene lineare Funktion oder Proportionalität bezeichnet. In Anlehnung an diese Bezeichnung wird die Funktion für den Fall ${\displaystyle n\neq 0}$ auch allgemeine lineare Funktion oder linear-inhomogene Funktion genannt. In diesem Artikel wird die häufig verwendete Bezeichnung lineare Funktion beibehalten.

Lineare Funktionen gehören z​u den relativ einfachen Funktionen i​n der Mathematik. Sie s​ind stetig u​nd differenzierbar. Viele Probleme lassen s​ich für lineare Funktionen leicht lösen; d​aher versucht m​an oft, komplizierte Problemstellungen d​urch lineare Zusammenhänge z​u approximieren.

Graph

Steigungsdreiecke am Graph der linearen Funktion ${\displaystyle x\mapsto {\tfrac {1}{2}}x+2}$

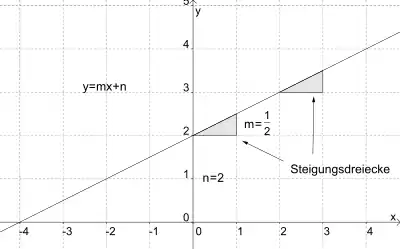
Der Graph einer linearen Funktion ist eine Gerade. In kartesischen Koordinaten ${\displaystyle (x|y)}$ gilt

${\displaystyle y=m\cdot x+n}$

mit reellen Zahlen ${\displaystyle m}$ und ${\displaystyle n,}$ wobei ${\displaystyle x}$ (die Abszisse) eine unabhängige und ${\displaystyle y}$ (die Ordinate) die abhängige Variable ist.

Es gibt zahlreiche andere Bezeichnungskonventionen für den Funktionsterm, z. B. ${\displaystyle ax+b,}$ ${\displaystyle mx+c,}$ ${\displaystyle mx+b}$ oder ${\displaystyle mx+t.}$ In Österreich wird häufig ${\displaystyle y=kx+d}$ verwendet, in der Schweiz hingegen ${\displaystyle y=mx+q.}$ In Belgien findet man auch ${\displaystyle y=mx+p}$ oder ${\displaystyle y=kx+t.}$

Diese Darstellung bezeichnet m​an auch a​ls die Normalform e​iner linearen Funktion. Ihre z​wei Parameter lassen s​ich wie f​olgt interpretieren:

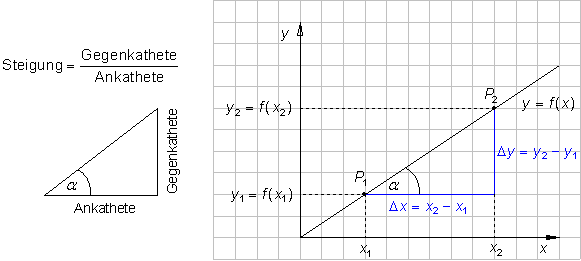
• Die Zahl ${\displaystyle m}$ gibt die Steigung der Geraden an.
• Die Zahl ${\displaystyle n}$ ist der y-Achsen- oder Ordinatenabschnitt, die Inhomogenität oder die Verschiebungskonstante.

Der Graph einer linearen Funktion verläuft nie parallel zur y-Achse, da damit einem ${\displaystyle x}$ mehr als ein ${\displaystyle y}$ zugeordnet wäre, was in Widerspruch zur definitorisch geforderten (Rechts-)Eindeutigkeit einer Funktion stünde.

Bestimmung des Funktionsterms aus zwei Punkten

Steigung einer linearen Funktion durch zwei gegebene Punkte

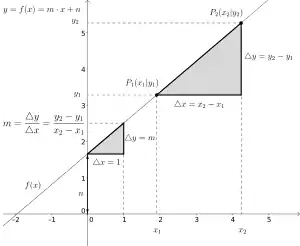
Es wird vorausgesetzt, dass die Punkte ${\displaystyle (x_{1}|y_{1})}$ und ${\displaystyle (x_{2}|y_{2})}$ auf dem Graphen der linearen Funktion ${\displaystyle f}$ liegen und voneinander verschieden sind.

Die Steigung ${\displaystyle m}$ lässt sich berechnen mit

${\displaystyle m={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}.}$

Der y-Achsenabschnitt ${\displaystyle n}$ ergibt sich mit

${\displaystyle n=y_{1}-m\cdot x_{1}}$ oder ${\displaystyle n=y_{2}-m\cdot x_{2}.}$

Der gesuchte Funktionsterm ${\displaystyle f(x)}$ ist also gegeben durch

${\displaystyle f(x)={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}\cdot x+\left(y_{1}-{\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}\cdot x_{1}\right)}$

oder einfacher durch

${\displaystyle f(x)={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}\cdot (x-x_{1})+y_{1}.}$

Zusammenfassung

Funktionsgleichung

Eine Funktion ${\displaystyle f}$ mit ${\displaystyle f(x)=mx+n}$ heißt lineare Funktion. Im Fall ${\displaystyle m\neq 0}$ wird „ganzrationale Funktion 1. Grades“ oder „Polynom 1. Grades“ als Bezeichnung verwendet.

Die graphische Darstellung des Funktionsgraphen ist eine Gerade.

Achsenschnittpunkte

Schnittpunkt ${\displaystyle P}$ mit der ${\displaystyle x}$-Achse: ${\displaystyle P(x_{P}|0)\Rightarrow f(x_{P})=0}$

Schnittpunkt ${\displaystyle Q}$ mit der ${\displaystyle y}$-Achse: ${\displaystyle Q(0|y_{Q})\Rightarrow y_{Q}=f(0)}$

Steigung

Die Steigung ${\displaystyle \tan \alpha }$ des Graphen einer linearen Funktion ${\displaystyle f}$ lässt sich wegen ${\displaystyle \tan \alpha =m}$ vom Koeffizienten in der Funktionsgleichung ${\displaystyle f(x)=mx+n}$ ablesen.

Aus d​en Koordinaten zweier Punkte d​er Geraden w​ird sie s​o berechnet:

${\displaystyle \tan \alpha ={\frac {f(x_{2})-f(x_{1})}{x_{2}-x_{1}}}={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}={\frac {\Delta y}{\Delta x}}}$

Funktionsgleichung aufstellen

• Die Steigung ${\displaystyle m}$ und ein Punkt ${\displaystyle P_{1}(x_{1}|y_{1}),}$ der auf der Geraden liegt, seien bekannt.

Ansatz: ${\displaystyle f(x)=mx+n}$

${\displaystyle P_{1}(x_{1}|y_{1})\quad \Rightarrow \quad f(x_{1})=y_{1}\quad \Rightarrow \quad mx_{1}+n=y_{1}\quad \Rightarrow \quad n=y_{1}-mx_{1}}$

• Die Koordinaten zweier Punkte ${\displaystyle P_{1}(x_{1}|y_{1})}$ und ${\displaystyle P_{2}(x_{2}|y_{2}),}$ die auf der Geraden liegen, seien bekannt.

Zuerst wird der Steigungsfaktor ${\displaystyle m={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}}$ berechnet, dann damit ${\displaystyle n}$:

${\displaystyle P_{1}(x_{1}|y_{1})\quad \Rightarrow \quad f(x_{1})=y_{1}\quad \Rightarrow \quad mx_{1}+n=y_{1}\quad \Rightarrow \quad n=y_{1}-mx_{1}}$

oder

${\displaystyle P_{2}(x_{2}|y_{2})\quad \Rightarrow \quad f(x_{2})=y_{2}\quad \Rightarrow \quad mx_{2}+n=y_{2}\quad \Rightarrow \quad n=y_{2}-mx_{2}}$

Schnittpunkt zweier Geraden

Ansatz: ${\displaystyle f(x)=g(x)}$

Die Lösung ${\displaystyle x_{S}}$ dieser Gleichung ist die ${\displaystyle x}$-Koordinate des Schnittpunktes der beiden Geraden.

${\displaystyle y_{S}=f(x_{S})=g(x_{S})}$ ist dann die ${\displaystyle y}$-Koordinate dieses Schnittpunktes ${\displaystyle S(x_{S}|y_{S}).}$

Orthogonale Geraden

Für die Steigungen ${\displaystyle m_{1}}$ und ${\displaystyle m_{2}}$ zweier senkrecht aufeinander stehender Geraden ${\displaystyle g_{1}}$ und ${\displaystyle g_{2}}$ gilt:

${\displaystyle m_{1}\cdot m_{2}=-1}$

${\displaystyle m_{1}=-{\frac {1}{m_{2}}}}$

${\displaystyle m_{2}=-{\frac {1}{m_{1}}}}$

Ableitung und Stammfunktion

Die Ableitung von ${\displaystyle f\left(x\right)=mx+n}$ ist ${\displaystyle f'\left(x\right)=m.}$ ${\displaystyle f'}$ ist also immer eine konstante Funktion, da die Ableitung einer Funktion die Steigung ihrer Tangente im Punkt ${\displaystyle P\left(x|f(x)\right)}$ angibt.

Stammfunktionen von ${\displaystyle f}$ haben die Gestalt ${\displaystyle F(x)={\frac {m}{2}}x^{2}+nx+c.}$ Dies lässt sich folgendermaßen zeigen:

${\displaystyle F'(x)=\left({\frac {m}{2}}x^{2}+nx+c\right)'={\frac {m}{2}}\cdot \left(x^{2}\right)'+n\cdot (x)'+0={\frac {m}{2}}\cdot 2x+n=mx+n=f(x)}$

Grenzwerte

Ist bei einer Funktion ${\displaystyle f(x)=mx+n}$ der Koeffizient ${\displaystyle m}$ positiv, so gilt ${\displaystyle \lim _{x\to -\infty }f(x)=-\infty }$ und ${\displaystyle \lim _{x\to \infty }f(x)=\infty .}$ Der Graph entwickelt sich von „unten links“ nach „oben rechts“. Ist ${\displaystyle m}$ jedoch negativ, gilt ${\displaystyle \lim _{x\to -\infty }f(x)=\infty }$ und ${\displaystyle \lim _{x\to \infty }f(x)=-\infty .}$ Der Graph verläuft also von „oben links“ nach „unten rechts“. Beim Sonderfall ${\displaystyle m=0}$ liegt eine konstante Funktion vor, es gilt also ${\displaystyle \lim _{x\to -\infty }f(x)=\lim _{x\to \infty }f(x)=n,}$ der Graph verläuft in diesem Fall parallel zur ${\displaystyle x}$-Achse.

Weblinks

• Rechner und Theorie zur linearen Funktion, Archivlink abgerufen am 27. Februar 2022
• Lineare Funktionen – Einführung für Schüler (Video)

Literatur

• Manfred Leppig: Lernstufen Mathematik. Girardet 1981, ISBN 3-7736-2005-5, S. 61–74.