Neutroneneinfang

Neutroneneinfang (Bezeichnung in der Kernphysik und Kerntechnik; engl. neutron capture) oder Neutronenanlagerung (Bezeichnung in der Astrophysik) ist im engeren Sinne eine Kernreaktion, bei der ein Atomkern ein Neutron absorbiert, ohne dass dabei Teilchen mit Masse freigesetzt werden. Der Kern gibt die gewonnene Bindungsenergie vielmehr als Gammastrahlung ab. Nach seiner Formelschreibweise – Beispiele siehe unten – wird dieser Reaktionstyp auch n-gamma-Reaktion genannt.[1]

Allerdings werden gelegentlich auch Neutronenreaktionen mit Emission von Masseteilchen als Neutroneneinfang bezeichnet, besonders dann, wenn ihre Anregungsfunktion jener der n-gamma-Reaktionen ähnelt. Dies gilt beispielsweise für die n-alpha-Reaktion an Bor-10, wie etwa die Bezeichnung Bor-Neutroneneinfangtherapie zeigt.

Nuklidkarte mit Wirkungsquerschnitt für Neutroneneinfang

Da das Neutron im Gegensatz zum Proton keine elektrische Ladung trägt und daher vom Atomkern nicht abgestoßen wird, kann es sich ihm auch mit geringer Bewegungsenergie leicht nähern. Der Wirkungsquerschnitt für den Einfang ist sogar im Allgemeinen bei thermischer, also sehr kleiner, Neutronenenergie besonders groß.

In Sternen läuft die Neutronenanlagerung als s- oder r-Prozess ab. Sie spielt in der kosmischen Nukleosynthese eine wichtige Rolle, denn sie erklärt die Entstehung der Elemente mit Massenzahlen oberhalb etwa 60, also der Atome, die schwerer als Eisen- oder Nickelatome sind. Diese können durch thermonukleare Reaktionen, d. h. durch Kernfusion, in Sternen nicht gebildet werden.

In normaler Umgebung auf der Erde freigesetzte Neutronen werden in den allermeisten Fällen, nachdem sie auf thermische Energie abgebremst sind, von Kernen in dieser Weise eingefangen. Technische Anwendungen des Neutroneneinfangs sind beispielsweise:

Steuerung von Kernreaktoren und Abschirmung gegen Neutronenstrahlung (siehe Neutronenabsorber),
Gewinnung bestimmter Radionuklide.

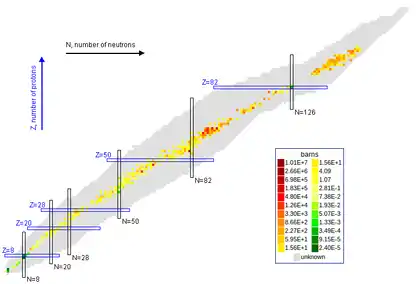
Das nebenstehende Bild zeigt eine Nuklidkarte mit farblicher Kennzeichnung des Wirkungsquerschnitts für Neutroneneinfang (Neutroneneinfangsquerschnitt). Durch Doppellinien hervorgehoben sind die magischen Protonen- und Neutronenzahlen; man erkennt, dass dieser Wirkungsquerschnitt bei solchen magischen Atomkernen meist klein, fern von magischen Zahlen dagegen groß ist.

Neutroneneinfang bei kleinem Neutronenfluss

Bei nicht zu hohem Neutronenfluss, etwa bei Neutronenbestrahlung in einem Kernreaktor, wird jeweils ein Neutron von einem Atomkern eingefangen. Die Massenzahl (Zahl der Nukleonen im Kern) steigt dadurch um 1. Beispielsweise entsteht bei Bestrahlung von natürlichem Gold, ¹⁹⁷Au, das Goldisotop ¹⁹⁸Au in einem hochangeregten Zustand, der sehr schnell durch Aussendung eines γ-Quants zum Grundzustand des ¹⁹⁸Au übergeht. In Formelschreibweise:

\mathrm {{^{197}_{\ 79}Au}+n\rightarrow {^{198}_{\ 79}Au}} +\gamma

oder kurz:

\mathrm {^{197}Au(n,\gamma )^{198}Au}

Das Goldisotop ¹⁹⁸Au ist ein β⁻-Strahler, sein Kern zerfällt also durch Emission eines Elektrons und eines Elektron-Antineutrinos zu dem Quecksilberisotop ¹⁹⁸Hg.

Der oben erwähnte s-Prozess im Inneren von Sternen läuft im Wesentlichen genauso ab.

Bedeutung in der Kerntechnik

Am gewöhnlichen Wasserstoff gibt es eine Einfangreaktion mit merklichem Wirkungsquerschnitt:

\mathrm {^{1}H(n,\gamma )^{2}H} +2,2\,\mathrm {MeV}

.

Diese Absorption am Wasserstoff bewirkt, dass ein Leichtwasserreaktor mit Natururan nicht kritisch werden kann. Dieses Problem wurde umgangen durch Urananreicherung oder durch den Bau von Schwerwasserreaktoren sowie graphitmoderierten Reaktoren.

Auch die zur Reaktorsteuerung und in Abschirmungen gegen Neutronen verwendeten Neutronenabsorber beruhen meist auf Neutroneneinfang.

Im Kernbrennstoff Uran bilden sich durch Neutroneneinfang Transurane, vor allem Plutonium - im Brutreaktor intendiert, sonst eher als Nebenprodukt. Ein erheblicher Teil der besonders stark radioaktiven langlebigen nuklearen Abfälle entsteht durch (wiederholten) Neutroneneinfang. Neben den Auswirkungen auf die Endlagerfähigkeit unterscheidet sich auch die Spaltbarkeit der entstandenen Isotope teilweise deutlich vom ursprünglichen Kernbrennstoff.

Neutroneneinfang bei großem Neutronenfluss

Beim r-Prozess im Sterninnern ist die Neutronenflussdichte so hoch, dass der Atomkern zwischen den Neutroneneinfängen „keine Zeit“ für den Betazerfall hat, d. h., der mittlere Zeitabstand zwischen den Neutroneneinfängen ist kurz im Vergleich zur Halbwertszeit des Betazerfalls. Die Massenzahl nimmt dadurch stark zu, ohne dass die Ordnungszahl steigt. Erst anschließend zerfallen die entstandenen hoch instabilen Nuklide durch jeweils mehrere aufeinander folgende β⁻-Zerfälle zu stabilen oder stabileren (langlebigeren) Nukliden mit entsprechend höheren Ordnungszahlen.

Siehe auch

Protonenanlagerung

Literatur

Bogdan Povh, Klaus Rith, Christoph Scholz, Frank Zetsche: Teilchen und Kerne. 4. Auflage, Springer 1997, ISBN 3-540-61737-X.
Arnold Hanslmeier: Einführung in Astronomie und Astrophysik. 2. Auflage, Spektrum Akademischer Verlag, 2007, ISBN 978-3-8274-1846-3.

Einzelnachweise

Vgl. B. L. Cohen, Concepts of Nuclear Physics, McGraw-Hill 1971, S. 338.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Vgl. B. L. Cohen, Concepts of Nuclear Physics, McGraw-Hill 1971, S. 338.