Insolvenzprognoseverfahren

Als Insolvenzprognoseverfahren werden in der Finanzanalyse und im Bankwesen Verfahren bezeichnet, welche das Insolvenzrisiko und damit die Wahrscheinlichkeiten bestimmen, mit denen Wirtschaftssubjekte innerhalb eines bestimmten Zeitraums (typischerweise ein Jahr) insolvent werden.

Allgemeines

Die folgenden Ausführungen beziehen sich auf Verfahren für die Prognose von Unternehmensinsolvenzen.[1] Als Wirtschaftssubjekte kommen Unternehmen, Privatpersonen, Staaten oder sonstige Institutionen in Frage.

Entwicklung der Unternehmensinsolvenzen in Deutschland

Während zu Beginn der 1990er Jahre in Deutschland noch rund 10.000 Unternehmensinsolvenzen pro Jahr zu verzeichnen waren, stieg deren Zahl bis 2003/2004 auf fast 40.000 an. Bei einem Unternehmensbestand von rund drei Millionen entsprach dies einer durchschnittlichen Insolvenzquote von 1,3 % pro Jahr. Je nach Unternehmenssegment waren deutlich höhere Werte zu verzeichnen. In den Folgejahren verringerte sich die Anzahl der Insolvenzen wieder etwas und betrug im Zeitraum 2007 bis 2011 jeweils rund 30.000. Die Höhe der neu entstandenen offenen Insolvenzforderungen betrug Anfang der 1990er Jahre noch rund 6 Milliarden EUR pro Jahr, in den 2000er Jahren hingegen meist zwischen 30 und 40 Milliarden EUR, in einzelnen Jahren (2002 und 2009) wurden sogar Werte von 62 bzw. 85 Milliarden EUR erreicht. Insolvenzforderungen sind erfahrungsgemäß zu 90 bis 95 % uneinbringbar.[2]

Motivation für die Entwicklung

Der Fähigkeit zur Erstellung trennscharfer Prognosen von Unternehmensinsolvenzen, aber auch der Fähigkeit zur Ermittlung von Handlungsempfehlungen zur Vermeidung von Insolvenzen kommt sowohl aus individueller als auch aus volkswirtschaftlicher Sicht eine große Bedeutung zu. Auf individueller Ebene sind neben Eigentümern, Mitarbeitern, Kunden, Lieferanten, Wirtschaftsprüfern und sonstigen Geschäftspartnern eines Unternehmens vor allem Banken an präzisen Insolvenzprognosen interessiert, da sie bei Unternehmensinsolvenzen regelmäßig erhebliche Schäden zu verzeichnen haben.[3][4] Allein die administrativen Aufwendungen (Konkursverwalter) und Kosten, die mit der Liquidation der Aktiva des insolventen Unternehmens verbunden sind, verzehren im Durchschnitt zwischen 15 % und 20 % der Bruttoliquidationserlöse.[5]

Aus Bankensicht sind Insolvenzprognosen eine wesentliche Voraussetzung dafür, um eine risikogerechte Preissetzung und Ausgestaltung nichtfinanzieller Kreditkonditionen (Limite, geforderte Sicherheiten) umsetzen zu können. Es sind Kreditprozesse kostengünstig zu gestalten (durch die Identifikation kritischer Fälle, die einer aufwendigeren Betreuung durch Kreditexperten bedürfen), die eigene Liquidität durch die Schaffung von Verbriefungsmöglichkeiten zu erhöhen und der ökonomische bzw. aufsichtsrechtliche Eigenkapitalbedarf zu ermitteln und zu steuern.[6] Aus volkswirtschaftlicher Sicht werden Insolvenzprognoseverfahren als eine wichtige Voraussetzung für die Stabilität des Bankensystems gesehen. Überhöhte Kreditrisiken waren die häufigste Ursache der über 100 Bankinsolvenzen seit den 1960er Jahren in (West-)Deutschland.[7] Auch entfallen über 90 % der aufsichtsrechtlichen Eigenkapitalanforderungen bei Banken auf die Absicherung von Kreditrisiken.[8] Ferner ist die Verfügbarkeit leistungsfähiger Insolvenzprognoseverfahren eine notwendige Voraussetzung, um Kreditnehmer zu einem anreizkompatiblen, risikobewussten Verhalten zu motivieren.[9] Ebenso kann durch leistungsfähigere Insolvenzprognosen Marktversagen, im Sinne eines vollständigen Rückzugs von Banken oder anderen Fremdkapitalgebern aus der Finanzierung von Unternehmen in überdurchschnittlich riskanten Segmenten vermieden werden.[10]

Klassifikation

Der aktuelle Stand der Wissenschaft in der Insolvenzprognoseforschung ist durch Methodenvielfalt geprägt. Ein Grund für diese Vielfalt dürfte im Fehlen eines derzeit allgemein akzeptierten, umfassenden theoretischen Fundaments zur Erklärung von Unternehmensinsolvenzen liegen.[11] Ursächlich für die Vielfalt an Insolvenzprognosetechniken dürfte auch sein, dass zahlreiche Verfahren, die sich häufig bereits in anderen Kontexten als der Insolvenzprognose bewährt haben, als ungeeignet oder unterlegen verworfen werden kann. Ferner können – je nach prinzipieller Verfügbarkeit bzw. den jeweils akzeptierten Kosten der Informationserhebung – eine Vielzahl unterschiedlicher Datenquellen und Datenarten für die Zwecke der Insolvenzprognose herangezogen werden, deren Aggregation zum Teil unterschiedliche Verfahren bedingen bzw. aus statistisch-technischen Gründen als zweckmäßig erscheinen lassen.[12] Einen Überblick über die Vielzahl der in Wissenschaft und Praxis verwendeten Insolvenzprognoseverfahren zeigt die folgende Abbildung.[13]

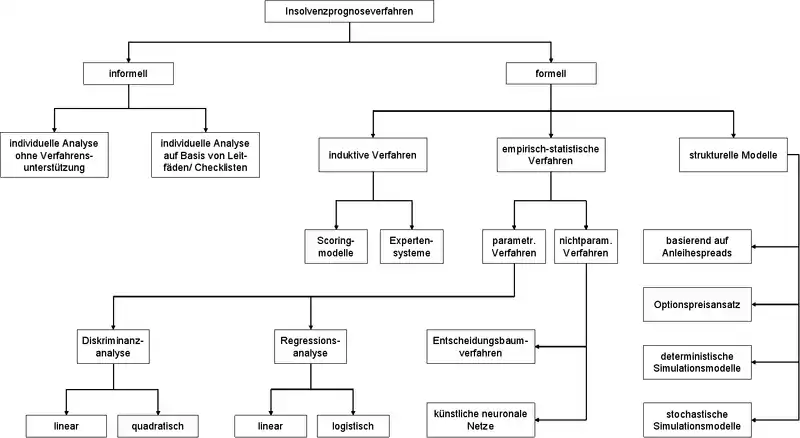
Übersicht Insolvenzprognoseverfahren

Insolvenzprognoseverfahren lassen sich in formelle und informelle Insolvenzprognoseverfahren untergliedern. Bei den informellen Verfahren treffen menschliche Kreditentscheider Insolvenzprognosen auf der Basis ihrer Intuition und persönlichen Erfahrung. Formelle Verfahren basieren hingegen auf explizit festgeschriebenen Verfahrensregeln. Bei den formellen Verfahren werden induktive, (parametrische und nichtparametrische) empirisch-statistische sowie strukturelle Verfahren unterschieden. Zu den induktiven Verfahren gehören beispielsweise Scoringmodelle und Expertensysteme. Bei den parametrischen empirisch-statistischen Verfahren sind die Multivariate Lineare Diskriminanzanalyse und die Logistische Regressionsanalyse von Bedeutung. Bei den nichtparametrischen empirisch-statistischen Insolvenzprognoseverfahren sind die Entscheidungsbaumverfahren und Künstliche neuronale Netze zu nennen. Zu den strukturellen Insolvenzprognosemodellen gehören anleihespreadbasierte und Optionspreismodelle sowie deterministische und stochastische Simulationsverfahren.

Das erste formelle, multivariate Insolvenzprognoseverfahren für Unternehmen war das Z-Faktormodell (Altman’s Z-Score) von Altman (1968), ein Diskriminanzanalysemodell.

Datenquellen

Übersicht

Zahlreiche Datenquellen können für die Prognose von Unternehmensinsolvenzen herangezogen werden. Je nach der Objektivität ihrer Erhebung („harte“ vs. „weiche“ Daten) und je nachdem, ob die entsprechenden Daten originär metrisch skaliert sind oder nicht („quantitative“ vs. „qualitative“ Daten), lassen sich insgesamt vier Gruppen von Inputvariablen für Insolvenzprognoseverfahren unterscheiden, siehe die folgende Abbildung.[14]

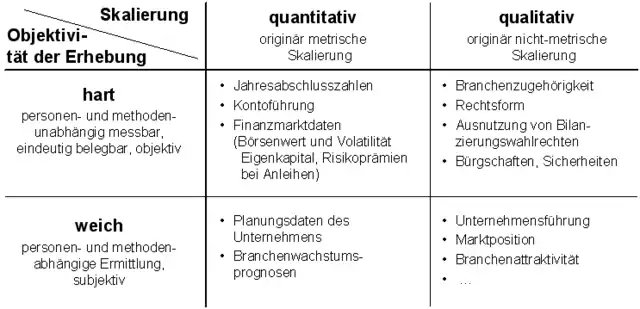
Datenquellen Insolvenzprognoseverfahren

Harte quantitative Daten

Harte quantitative Daten sind Daten, die originär metrisch skaliert sind und methoden- und personenunabhängig erhoben werden können. Von besonderer Relevanz im Kontext der Unternehmensinsolvenzprognose sind dabei Jahresabschlussdaten, Informationen zum Kontoführungsverhalten[15] sowie Finanzmarktdaten (Niveau und Volatilität der Marktkapitalisierung des Unternehmens, Höhe der Risikoprämie auf börsennotierte Fremdverbindlichkeiten des Unternehmens). Vorteile von Kontoführungs- und Marktdaten gegenüber Buchhaltungsdaten bestehen in der wesentlich größeren Aktualität. Sie können täglich aktualisiert werden und ihre Erhebung verursacht praktisch keine (zusätzlichen) Kosten. Auch können sie von den Unternehmen kaum manipuliert werden. Ein wichtiger Vorteil von Marktdaten gegenüber Kontoführungs- und Buchhaltungsdaten wird in deren „Vorwärtsgerichtetheit“ gesehen. Dabei wird unterstellt, dass Marktdaten – via den rationalen Erwartungen der Marktteilnehmer – von der künftigen Entwicklungen der Unternehmen beeinflusst werden und nicht von deren Vergangenheit – wie im Fall von Kontoführungs- und Buchhaltungsdaten.[16] Allerdings verfügen nur die wenigsten Unternehmen über börsennotierte Eigen- oder Fremdmittel. Angaben zum Kontoführungsverhalten stehen den jeweiligen kreditgebenden Banken exklusiv zur Verfügung – und auch diesen erst nachdem sie Kredite an die entsprechenden Unternehmen vergeben haben. Am besten ist die Datenlage bei Jahresabschlussdaten, welche Angaben zu den Bilanzen, den Gewinn- und Verlustrechnungen und den Anlagespiegeln umfassen. Jahresabschlussdaten zeichnen sich durch einen relativ geringen Erfassungsaufwand aus. Ihre Erhebung erfordert keine besonderen Kenntnisse. Ihre Erhebung unterliegt keinen subjektiven Einflüssen und bietet keine Möglichkeiten zur gezielten Manipulation, die sich nicht leicht durch nachträgliche Kontrollen zweifelsfrei feststellen ließen.[17] Eingabefehler lassen sich aufgrund der Redundanten Datenstruktur leicht erkennen und beheben. Auch lassen sich durch systematische Auswertungen der Jahresabschlussunterlagen, „wobei neben Bilanz und GuV insbesondere die zusätzlichen Erläuterungen im Anhang und Lagebericht heranzuziehen sind“[18], viele der Möglichkeiten aufdecken – und ggf. später neutralisieren, mit denen die Ertrags- und Vermögenslage des Unternehmens gezielt verzerrt werden soll.

Harte qualitative Daten

Harte qualitative Daten sind nominal oder ordinal skalierte Daten, die personen- und methodenunabhängig messbar sind und damit objektiv erhoben werden können. Im Rahmen empirisch-statistischer Verfahren werden dabei Faktoren aufgedeckt, die einen empirischen Zusammenhang mit der Ausfallwahrscheinlichkeit der Unternehmen aufweisen („statistische Sippenhaft“[19]). Von besonderer Bedeutung sind in diesem Kontext die Rechtsform und die Branchenzugehörigkeit – denn die verschiedenen Branchen-Rechtsform-Gruppen sind durch erhebliche und langanhaltende Unterschiede bezüglich ihrer Insolvenzquoten gekennzeichnet. So zeigt sich beispielsweise, dass Kapitalgesellschaften des Baugewerbes in Deutschland über lange Zeiträume hinweg etwa fünfzehnmal so große Insolvenzquoten zu verzeichnen hatten wie Einzelunternehmen des Dienstleistungsgewerbes.[20]

Weiche quantitative Daten

Weiche quantitative Daten sind metrisch skalierte Daten, deren Erhebung persönlichen, subjektiven Beurteilungen (seitens der Befragten oder der Befrager) unterliegt. Typische weiche quantitative Informationen im Kontext der Insolvenzprognose sind Branchenwachstumsprognosen, quantitative Angaben zu betrieblichen Risiken oder individuelle Angaben der Unternehmen, welche die für künftige Perioden geplanten Umsätze, Kosten oder Gewinne betreffen. Eigene Untersuchungen mit mittelständischen Unternehmen zeigten jedoch, dass die Mehrzahl der Unternehmen keine (konsistenten) Mehrjahresfinanzpläne erstellt. Die von den Unternehmen gemachten Planangaben sind im Durchschnitt erheblich positiv verzerrt. Sie können vermutlich nur im Sinne von "angestrebten Zielgrößen" interpretiert werden, stellen aber keine Erwartungswerte im statistischen Sinne dar. Häufig werden runde Werte genannt. Die Eintrittswahrscheinlichkeiten von bestandsgefährdenden Verlusten werden völlig unterschätzt. Besonders problematisch ist, dass die Planangaben je nach Art der Befragung erhebliche Widersprüche aufweisen. Nachteilig ist ferner, dass die Erhebung detaillierter Planungsdaten zeitaufwendig und teuer ist, da hierbei eine Vielzahl an Daten in einer für die Unternehmen ungewohnten und erklärungsbedürftigen Form im Rahmen von Vor-Ort-Gesprächen erhoben werden müssen.

Auch ist nicht zu erwarten, dass die Unternehmen ihre Plan- und Risikoinformationen gegenüber Dritten, insbesondere gegenüber Banken oder Auskunfteien, wahrheitsgemäß und umfassend offenlegen, wenn sie damit rechnen müssen, dass dies negative wirtschaftliche Konsequenzen für sie haben kann. Einer nachträglichen Sanktionierung „falscher“ Plan- und Risikoannahmen sind enge Grenzen gesetzt. Für die Verfehlung geplanter Umsatz- oder Ertragsziele lassen sich im Nachhinein immer plausible Gründe vorbringen, die nicht im Einflussbereich des Unternehmens liegen. Stochastische Planannahmen lassen sich, außer in trivialen Fällen, ex-post nie mit Sicherheit als wahr oder falsch klassifizieren. Auch würde die Sanktionierung von Planverfehlungen (zusätzliche) Anreize zu ökonomisch nutzlosen bis schädlichen Verhaltensweisen setzen, beispielsweise durch die Verschiebung von Umsätzen und/oder Kosten und Erträgen in benachbarte Perioden.

Weiche qualitative Daten

Weiche qualitative Daten sind Daten, die nicht originär metrisch skaliert sind und deren Erhebung subjektiven, wertenden Einflüssen unterliegt. Hierunter fallen beispielsweise Fragen zu den betrieblichen Erfolgspotentialen, wie der „Qualität des Rechnungswesens“, der „fachlichen Eignung des Managements“ oder der „Lieferantenabhängigkeit“.[21] Der Nutzen weicher qualitativer Daten im Kontext der Unternehmensinsolvenzprognose wird vor allem darin gesehen, dass sie es erlauben sollen, negative Unternehmensentwicklungen frühzeitig zu identifizieren, also noch bevor sie sich in „schlechten“ Jahresabschlüssen manifestieren.[22]

Weiche qualitative Faktoren können jedoch nur mit einer sehr geringen Reliabilität erhoben werden, was nur einen geringen (zusätzlichen) Prognosenutzen dieser Daten vermuten lässt.

Fazit zu Datenquellen

Die Ratingverfahren von Banken basieren typischerweise zu erheblichen Teilen auf der Auswertung harter quantitativer Informationen und dabei insbesondere auf der statistischen Analyse von aus Jahresabschlüssen abgeleiteten Kennzahlen.[23] Viele in wissenschaftlichen Studien vorgestellte Insolvenzprognosemodelle sowie die Prognosemodelle kommerzieller Anbieter, die zur kostengünstigen Bonitätsbeurteilung von mittelständischen Unternehmen entwickelt wurden, beschränken sich von vornherein ausschließlich auf die Analyse derartiger Finanzkennzahlen.[24] In einigen Ratingmodellen werden zusätzlich auch harte qualitative Variablen wie Branche, Rechtsform oder regionale Herkunft, berücksichtigt.

Auch wenn sie theoretisch viele Vorteile bieten, ist der praktische Nutzen ("zukunftsbezogener") weicher quantitativer und weicher qualitativer Daten für die Prognose von Insolvenzen gering. Ihre Erhebung verursacht vergleichsweise hohe Kosten und unterliegt Anreizproblemen seitens der Befragten.

Auch wenn die Ratingagenturen in Abrede stellen, dass die von ihnen vergebenen Urteile im Wesentlichen auf Kennzahlenanalysen beruhen[25], wurde in empirischen Studien zumindest gezeigt, dass sich die Ratingurteile renommierter Agenturen anhand von (wenigen) Finanzkennzahlen relativ gut reproduzieren bzw. prognostizieren lassen.[26] Interessant ist dabei auch, dass der erhebliche personelle Aufwand, den die kommerziellen Ratingagenturen bei der Erstellung ihrer Ratingurteile leisten[27] (und die erheblichen Gebühren, die sie hierfür in Rechnung stellen[28]) sich nicht adäquat in der Schätzgüte ihrer Prognosen niederschlägt. So lassen sich mit einfachen Kennzahlenmodellen – bei Anwendung auf identische Datensätze von Unternehmen – Insolvenzprognosen mit einer Qualität erstellen, die der Prognosequalität der Ratingurteile renommierter Agenturen entspricht oder diese sogar übertrifft.[29]

Klassifikation von Schätzgütemaßen

Unter der Schätzgüte eines Insolvenzprognoseverfahrens soll im Folgenden der Grad der Übereinstimmung der Insolvenzprognosen mit den tatsächlich eingetretenen Insolvenzereignissen verstanden werden. Mathematisch fassbare Präzisierungen des Begriffs müssen dabei berücksichtigen, ob die zu beurteilenden Insolvenzprognosen kategorialer (=nominaler), ordinaler oder kardinaler (=metrischer bzw. quantitativer) Art sind.

Als kategoriale Insolvenzprognosen werden Insolvenzprognosen bezeichnet, die lediglich zwei mögliche Ausprägungen zur Beurteilung der gerateten Unternehmen kennen: „Unternehmen A wird voraussichtlich (innerhalb eines zu spezifizierenden Zeitraums) ausfallen“ vs. „Unternehmen B wird voraussichtlich (innerhalb eines zu spezifizierenden Zeitraums) nicht ausfallen“.
Im Fall ordinaler Insolvenzprognosen werden Urteile über die relativen Ausfallwahrscheinlichkeiten der bewerteten Unternehmen abgegeben: „Unternehmen B fällt mit größerer Wahrscheinlichkeit (innerhalb eines zu spezifizierenden Zeitraums) aus als Unternehmen A, allerdings mit geringerer Wahrscheinlichkeit als Unternehmen C“. Zwar könnten ordinale Insolvenzprognosen theoretisch beliebig differenziert sein, in der Praxis haben sich aber ordinale Ratingsysteme durchgesetzt, die ihre Ergebnisse auf diskreten, 7- oder 17-stufigen Skalen in einer von Standard & Poor’s übernommenen Notation kommunizieren.[30]
Kardinale Insolvenzprognosen ordnen jedem Unternehmen eine Wahrscheinlichkeit zu, mit der das Unternehmen (innerhalb eines zu spezifizierenden Zeitraums) ausfällt.

Die einzelnen Verfahren sind abwärtskompatibel. Durch beliebige, schwach monotone Transformationen können aus Ausfallwahrscheinlichkeiten ordinal interpretierbare Scorewerte generiert werden, die sich bei Bedarf auch zu einer endlichen Anzahl von Klassen zusammenfassen lassen. Ebenso lassen sich durch Zusammenfassen von Scoreintervallen oder benachbarter Ratingklassen, solange bis nur noch zwei Klassen verbleiben, ordinale Insolvenzprognosen in kategoriale Insolvenzprognosen überführen. Die Art, in der Insolvenzprognosen vorliegen, ist unter anderem verfahrensbedingt. So generieren beispielsweise Diskriminanzanalysen oder Neuronale Netze standardmäßig nur kategoriale Insolvenzprognosen. Ihr Output wird in der Praxis jedoch auch ordinal interpretiert[31] und kann durch Kalibrierung auf Ausfalldaten auch einen kardinalen Informationsgehalt erhalten.[32]

Ordinale Insolvenzprognosen ergeben sich beispielsweise aus der Anwendung subjektiv parametrisierter Scoring- oder Kennzahlenmodelle, während mit Logit-Modellen kardinale Insolvenzprognosen erstellt werden. Die Art, in der Insolvenzprognosen vorliegen müssen, ergibt sich aus der beabsichtigten Nutzung der Prognosen: hat der Anwender lediglich zwei Handlungsoptionen – z. B. Annahme oder Ablehnung eines Kunden, positive oder negative Feststellung der „Notenbankfähigkeit“ von Forderungen[33] – so genügen im Prinzip kategoriale Insolvenzprognosen. Der optimalen Ausgestaltung kategorialer Prognosen liegt ein Zielkonflikt zwischen (Prognose-)Fehlern I. und Fehlern II. Art zugrunde (siehe Schätzgütemaße für kategoriale Insolvenzprognosen). Dieser wiederum ist abhängig von subjektiv beeinflussbaren Nebenbedingungen, beispielsweise der konkreten Ausgestaltung von Kreditkonditionen (Zinssätze, Sicherheiten, Bürgschaften, …) und von subjektiv nicht beeinflussbaren, aber im Zeitverlauf veränderlichen Größen, beispielsweise von der durchschnittlichen Ausfallquote der betrachteten Grundgesamtheit.[34]

An dieser Stelle setzen ordinale Gütemaße zur Beurteilung von Insolvenzprognosen an. Sie bewerten die Klassifikationsleistung von Insolvenzprognoseverfahren anhand der Gesamtheit aller möglichen mit dem Prognoseverfahren erzeugbaren Fehler-I-II-Kombinationen. Sie ermöglichen damit eine differenziertere Beurteilung von Kunden, beispielsweise als Grundlage für die Entscheidung über die Art und Höhe von jeweils einzufordernden Sicherheiten oder den festzulegenden Überwachungsaufwand. Beispiele für ordinale Schätzgütemaße sind die Accuracy Ratio (auch Gini-Index, Lorenz-Münzer-Konzentrationsmaß oder Power-Statistic).

Als Grundlage für quantitative Entscheidungen, beispielsweise für die Preisfindung von Krediten[35], Anleihen oder Derivaten oder für die Ermittlung des ökonomischen oder aufsichtsrechtlichen Risikokapitals werden hingegen kardinale Insolvenzprognosen, d. h. Ausfallwahrscheinlichkeiten, benötigt. So müssen gemäß den ab Anfang 2008 geltenden Neuen Eigenkapitalanforderungen des Basler Ausschusses für Bankenaufsicht bankinterne Ratingsysteme auf kardinalen Insolvenzprognosen (Ausfallwahrscheinlichkeiten) basieren.[36] Schätzgütemaße für kardinale Insolvenzprognosen sind beispielsweise der Brier-Score, die bedingte Informationsentropie, der Rommelfanger-Index oder der Gruppierte Brier-Score.[37]

Ein wesentlicher Nachteil kardinaler Schätzgütemaße ist deren Abhängigkeit von den erwarteten bzw. realisierten Portfolioausfallraten.[38] Sie eignen sich damit nicht für portfolioübergreifende Vergleiche – und schon bei moderat korrelierten Ausfallwahrscheinlichkeiten ist eine aussagekräftige Validierung kardinaler Insolvenzprognosen, selbst bei beliebig großen Portfolios, nicht mehr möglich.[39][40]

Insgesamt ist eine gute Trennfähigkeit von Insolvenzprognosen, wie sie durch ordinale Gütemaße gemessen werden, auch für die Qualität kardinaler Insolvenzprognosen wichtig – und sogar wichtiger als eine korrekte Kalibrierung.[41] Bei der Beurteilung der Qualität von Insolvenzprognosen wird deshalb im Folgenden schwerpunktmäßig Bezug auf ordinale Schätzgütemaße für Prognosen genommen.[42]

Literatur

E. I. Altman: Financial Ratios, Discriminant Analysis and the Prediction of Corporate Bankruptcy. (PDF-Datei; 1,19 MB). In: Journal of Finance. Band 23, Nr. 4, 1968, S. 589–610.
E. I. Altman, A. Saunders: Credit Risk Measurement: Developments over the last 20 years. In: Journal of Banking and Finance. Band 21, 1998, S. 1721–1742.
E. I. Altman, H. A. Rijken: How rating agencies achieve rating stability. In: Journal of Banking and Finance. Band 28, 2004, S. 2679–2714.
J. D. Amato, CH Furfine: Are credit ratings procyclical? (PDF-Datei; 327 kB). In: Journal of Banking and Finance. Band 28, 2004, S. 2641–2677.
S. Balcaen, H. Ooghe: 35 Years of Studies on Business Failure: An Overview of the Classic Statistical Methodologies and their Related Problems. Vlerick Leuven Gent Working Paper Series 2004/15, 2004. (auch in British Accounting Review. Band 38, Nr. 1, 2006, S. 63–93).
Basler Ausschuss für Bankenaufsicht (Hrsg.): Range of Practice in Banks' Internal Ratings systems. (PDF-Datei; 172 kB). Diskussionspapier, Bank für internationalen Zahlungsausgleich (BIS), 01/2000.
Basler Ausschuss für Bankenaufsicht (Hrsg.): Credit Ratings and Complementary Sources of Credit Quality Information. (PDF-Datei; 864 kB). Working Paper #3, 2000.
Basler Ausschuss für Bankenaufsicht (Hrsg.): Internationale Konvergenz der Kapitalmessung und Eigenkapitalanforderungen, Überarbeitete Rahmenvereinbarung. Übersetzung der Deutschen Bundesbank, 06/2004.
Basler Ausschuss für Bankenaufsicht (Hrsg.): Studies on the Validation of Internal Rating Systems. (PDF-Datei; 491 kB). Working Paper No. 14, überarbeitete Version, 05/2005.
M. Bemmann: Verbesserung der Vergleichbarkeit von Schätzgüteergebnissen von Insolvenzprognosestudien. In: Dresden Discussion Paper Series in Economics. 08/2005.
M. Bemmann: Entwicklung und Validierung eines stochastischen Simulationsmodells für die Prognose von Unternehmensinsolvenzen. Dissertation. Technische Universität Dresden, TUDpress Verlag der Wissenschaften, Dresden 2007, ISBN 978-3-940046-38-3.
S. Blochwitz, T. Liebig, M. Nyberg: Benchmarking Deutsche Bundesbank’s Default Risk Model, the KMV® Private Firm Model® and Common Financial Ratios for German Corporations. (PDF-Datei; 587 kB). Workshop on Applied Banking Research, Basler Ausschuss für Bankenaufsicht, 2000.
U. Blum, W. Gleißner, F Leibbrand: Stochastische Unternehmensmodelle als Kern innovativer Ratingsysteme. IWH-Diskussionspapier Nr. 6, 11/2005.
M. E. Blume, F. Lim, A. C. Mackinlay: The Declining Credit Quality of U.S. Corporate Debt: Myth or Reality. In: Journal of Finance. Band 53, Nr. 4, 1998, S. 1389–1413.
R. Cantor, C. Mann: Measuring the Performance of Corporate Bond Ratings. (PDF-Datei; 278 kB). Special Comment, Report #77916, Moody’s Investor’s Service, 04/2003.
M. S. Carey, M. Hrycay: Parameterizing Credit Risk Models with Rating Data. In: Journal of Banking and Finance. Band 25, Nr. 1, 2001, S. 197–270.
L. K. C. Chan, J. Karceski, J. Lakonishok: The Level and Persistence of Growth Rates. (PDF; 299 kB). In: Journal of Finance. Band 58, Nr. 2, 2003, S. 643–684.
Deutsche Bundesbank (Hrsg.): Zur Bonitätsbeurteilung von Wirtschaftsunternehmen durch die Deutsche Bundesbank. In: Monatsbericht Januar 1999. 01/1999, S. 51–64.
Deutsche Bundesbank (Hrsg.): Validierungsansätze für interne Ratingsysteme. In: Monatsbericht September 2003. 09/2003, S. 61–74.
Deutsche Bundesbank (Hrsg.): Finanzstabilitätsbericht 2005. 11/2005.
A. I. Dimitras, S. H. Zanakis, C. Zoponidis: A survey of business failures with an emphasis on prediction methods and industrial applications, Theory and methodology. In: European Journal of Operational Research. Band 90, 1996, S. 487–513.
J. Eigermann: Quantitative Credit-Ratingverfahren in der Praxis. In: Finanz Betrieb. 10/2001, S. 521–529.
B. Engelmann, E. Hayden, D. Tasche: Measuring the Discriminative Power of Rating Systems. Deutsche Bundesbank, Discussion Paper, Series 2: Banking and Financial supervision, 01/2003.
W. B. English, W. R. Nelson: Bank Risk Rating of Business Loan. Board of Governors of the Federal Reserve System FEDS Paper No. 98-51, 12/1998
P. Escott, F. Glormann, A. E. Kocagil: RiskCalcTM for Private Companies: The German Model. Moody’s KMV, Modeling Methodology, 11/2001.
E. Falkenstein, A. Boral, A. E. Kocagil: RiskCalcTM for Private Companies II: More Results and the Australian Model In: Moody’s Investors Service. Rating Methodology, Report # 62265, 12/2000
A. Fischer: Qualitative Merkmale in bankinternen Ratingsystemen: eine empirische Analyse zur Bonitätsbeurteilung von Firmenkunden. Dissertation, Universität Münster. Uhlenbruch Verlag, Bad Soden am Taunus 2004, ISBN 3-933207-47-9.
J. S. Fons, J. Viswanathan: A User’s Guide to Moody’s Default Predictor Model: an Accounting Ratio Approach. (PDF-Datei; 209 kB). In: Moody’s Investors Service. Report # 90127, 12/2004.
J. Franks, A. de Servigny, S. Davydenko: A Comparative Analysis of the Recovery Process and Recovery Rates for Private Companies in the U.K., France, and Germany. In: Standard and Poor’s Risk Solution. 06/2004.
S. Fritz, D. Hosemann: Restructuring the Credit Process: Behaviour Scoring for German Corporates. In: International Journal of Intelligent Systems in Accounting, Finance and Management. Band 9, 2000, S. 9–21.
H. Frydman, E. I. Altman, D. L. Kao: Introducing Recursive Partitioning for Financial Classification: The Case of Financial Distress. In: Journal of Finance. Band 40, Nr. 1, 1985, S. 269–291.
W. Gleißner: Ratingprognose, Solvenztest und Rating-Impact-Analyse. In: KRP Kredit & Rating Praxis. Ausgabe 03/2009, S. 38–40. (werner-gleissner.de)
J. Grunert, L. Norden, M. Weber: The role of non-financial factors in internal credit ratings. In: Journal of Banking and Finance. Band 29, 2005, S. 509–531.
T. Günther, M. Grüning: Einsatz von Insolvenzprognoseverfahren bei der Kreditwürdigkeitsprüfung im Firmenkundenbereich. In: Die Betriebswirtschaft. Heft 1/2000, S. 39–59.
T. Günther, G. Hübl, M. Niepel: Insolvenzprognose anhand unterjähriger Daten. In: Deutsches Steuerrecht. (DStR), Jg. 2000, Nr. 8, 2000, S. 346–352.
G. M. Gupton, R. M. Stein: LossCalc V2: Dynamic Prediction of LGD Modeling Methodology. Moody’s KMV, Working Paper, 01/2005.
A. Hamerle, R. Rauhmeier, D. Rösch: Uses and Misuses of Measures for Credit Rating Accuracy. Version 04/2003, Working Paper, University of Regensburg, 2003.
T. Hartmann-Wendels, A. Lieberoth-Leden, T. Mählmann, I. Zunder: Entwicklung eines Ratingsystems für mittelständische Unternehmen und dessen Einsatz in der Praxis. (PDF-Datei; 485 kB). In: Zeitschrift für Betriebswirtschaft. ZfB, Sonderheft 52, 2005, S. 1–29.
S. Huschens, S. Höse: Sind interne Ratingsysteme im Rahmen von Basel II evaluierbar? – Zur Schätzung von Ausfallwahrscheinlichkeiten durch Ausfallquoten. In: Zeitschrift für Betriebswirtschaft. (ZfB), Band 73, Nr. 2, 2003, S. 139–168.
K. Keasey, R. Watson: Financial Distress Prediction Models: A Review of their Usefulness. In: British Journal of Management. Band 2, 1991, S. 89–102.
KfW Bankengruppe (Hrsg.): Unternehmensfinanzierung: Immer noch schwierig, aber erste Anzeichen einer Besserung. Studie der KfW-Bankengruppe, 2005.
W. Krämer: Die Bewertung und der Vergleich von Kreditausfall-Prognosen. In: Kredit und Kapital. Band 36, Nr. 3, 2003, S. 395–410.
K. Küting, C.-P. Weber: Die Bilanzanalyse, Lehrbuch zur Beurteilung von Einzel- und Konzernabschlüssen. 7. Auflage. Schäffer-Pöschel, Stuttgart 2004, ISBN 3-7910-2260-1.
W.-C. Lee: Probabilistic Analysis of Global Performances of Diagnostic Tests: Interpreting the Lorenz Curve-Based Summary Measures. In: Statistics in Medicine. Band 18, 1999, S. 455–471.
B. Lehmann: Is It Worth the While? The Relevance of Qualitative Information in Credit Rating. EFMA 2003 Helsinki Meetings, 04/2003.
J. A. McQuown: A Comment on Market vs. Accounting-Based Measures of Default Risk. KMV Working Paper, KMV Corporation, 1993.
Moody’s (Hrsg.): Default & Recovery Rates of Corporate Bond Issuers, A Statistical Review of Moody’s Ratings Performance, 1920–2003. (PDF-Datei; 1,51 MB). Moody’s Investors Service, Special Comment, 01/2004.
Österreichische Nationalbank (Hrsg.): Ratingmodelle und -validierung. (PDF; 2,3 MB). Leitfadenreihe zum Kreditrisiko, Wien 2004.
Österreichische Nationalbank (Hrsg.): Kreditvergabeprozess und Kreditrisikomanagement. (PDF; 3,5 MB). Leitfadenreihe zum Kreditrisiko, Wien 2004.
F. Romeike, U. Wehrspohn: Marktstudie Rating-Software für Unternehmen. auszugsweise erschienen in RATINGaktuell 06/2004, S. 10–19.
H. Scheule: Prognose von Kreditausfallrisiken. Dissertation, Universität Regensburg. Uhlenbruch Verlag, Bad Soden/Ts. 2003, ISBN 3-933207-41-X.
J. R. Sobehart, R. M. Stein, V. Mikityanska, L. Li: Moody’s Public Firm Risk Model: A Hybrid Approach to Modeling Short Term Default Risk. Moody’s Investors Service, Rating Methodology, Report #53853, 03/2000.
R. H. Somers: A new asymmetric measure of association for ordinal variables. In: American Sociological Review. Band 27, Nr. 6, 1962, S. 799–811.
Standard and Poor’s (Hrsg.): Corporate Ratings Criteria. The McGraw Hills Companies, 2003.
Statistisches Bundesamt (Hrsg.): Insolvenzen in Deutschland 2003, Strukturen und Entwicklungen. Statistisches Bundesamt, Wiesbaden 2004.
R. M. Stein: Benchmarking Default Prediction Models, Pitfalls and Remedies in Model Validation. Moody’s KMV, Report #030124, 2002. (auch erschienen in Journal of Risk Model Validation, Band 1 (1), 2007, S. 77–113.)
J. A. Swets: Measuring the Accuracy of Diagnostic Systems. In: Science. Band 240, 1988, S. 1285–1293.
W. F. Treacy, M. S. Carey: Credit Risk Rating at Large U.S. Banks. (PDF-Datei; 138 kB). In: Journal of Banking and Finance. Band 24, Nr. 1–2, 2000, S. 167–201.
Unabhängiges Landeszentrum für Datenschutz Schleswig-Holstein (Hrsg.): Scoringsysteme zur Beurteilung der Kreditwürdigkeit - Chancen und Risiken für Verbraucher. (PDF; 7,2 MB). Studie im Auftrag des Bundesministeriums für Verbraucherschutz, Ernährung und Landwirtschaft bzw. der Bundesanstalt für Landwirtschaft und Ernährung, 2006.
L. J. White: The Credit Rating Industry: An Industrial Organization Analysis. New York University, Center for Law and Business, Research Paper No. 01-001, 04/2001.

Einzelnachweise

Dieser Artikel basiert wesentlich auf: Martin Bemmann, Verbesserung der Vergleichbarkeit von Schätzgüteergebnissen von Insolvenzprognosestudien, in: Dresden Discussion Paper Series in Economics. 08/2005; Martin Bemmann, Entwicklung und Validierung eines stochastischen Simulationsmodells für die Prognose von Unternehmensinsolvenzen, Dissertation, Technische Universität Dresden, TUDpress Verlag der Wissenschaften, Dresden, 2007
Zur Entwicklung der Insolvenzanzahl und -quoten sowie zum Bestand und zur Einbringbarkeit von Insolvenzforderungen siehe Statistisches Bundesamt (2004, S. 31 und S. 44), zu aktuellen Daten zum Insolvenzgeschehen siehe https://www.destatis.de/DE/ZahlenFakten/Indikatoren/LangeReihen/Insolvenzen/lrins01.html und https://www.destatis.de/DE/ZahlenFakten/Indikatoren/Konjunkturindikatoren/Insolvenzen/ins110.html (20. September 2012)
Siehe Dimitras, Zanakis, Zoponidis (1996, S. 488) und Balcaen, Ooghe (2004, S. 4) oder Hartmann-Wendels et al. (2005, S. 4f.) für eine Analyse der Interessenten an Insolvenzprognoseverfahren für Unternehmen.
siehe Franks, Servigny, Davydenko (2004, S. 4), Basler Ausschuss (2000b, S. 27f.), Basler Ausschuss (2000b, S. 7f.), Moody’s (2004, S. 13) und Gupton, Stein (2005).
siehe Franks, Servigny, Davydenko, 2004, S. 13
siehe English, Nelson (1998, S. 11f.), Treacy, Carey (2000, S. 897), Basler Ausschuss (2000a, S. 33), Escott, Glormann, Kocagil (2001a, S. 3) und Scheule (2003, S. 96ff.)
siehe Fischer (2004, S. 13 und die dort zitierte Literatur)
siehe Deutsche Bundesbank (2005, S. 44)
siehe Basler Ausschuss (2004, §4), OeNB (2004b, S. 33)
Siehe KfW (2005, S. 6): „Dies deutet auf die mittlerweile flächendeckende Verbreitung bankinterner Ratingtools hin, die nun auch bei kleinen Unternehmen Anwendung finden. […] Früher führten die für alle Kunden eines Kreditinstitutes weitgehend einheitlichen Zinssätze dazu, dass vor allem kleinere Unternehmen Schwierigkeiten hatten, überhaupt Kredite zu erhalten. Heute nutzen Banken und Sparkassen Ratingtools dazu, Kreditkonditionen zunehmend risikoorientiert zu gestalten. Damit wird insbesondere für kleine Unternehmen der Zugang zu Bankkrediten erleichtert.“
siehe Basler Ausschuss (2000b, S. 109ff.), Altman, Saunders (1998, S. 1724), Keasey, Watson (1991, S. 90) oder Günther, Hübl, Niepel (2000, S. 347).
siehe Frydman, Altman, Kao (1985, S. 270)
siehe Bemmann (2007, S. 6)
Die im Folgenden verwendete Terminologie wurde von Fischer (2004, S. 83) übernommen, der harte vs. weiche und quantitative vs. qualitative Daten abgrenzt. In der Insolvenzprognoseliteratur werden diese Begriffe meist synonym und deshalb häufig inkonsistent verwendet. Beispielsweise führt OeNB (2004a, S. 65) aus: „Qualitative Fragen unterliegen stets einem subjektiven Beurteilungsspielraum“, bezeichnet aber auch das zweifellos objektiv feststellbare „Heimatland des Schuldners“ als „qualitatives Ratingkriterium“, siehe OeNB (2004a, S. 66).
Für Kennzahlen zur Quantifizierung des Kontoführungsverhaltens siehe Fritz, Hosemann (2000, S. 13ff.).
Siehe bspw. McQuown (1993, S. 1f.). Gerade der Vorteil der „Vorwärtsgerichtetheit“ von Marktpreisen im Vergleich zu (historischen) Buchhaltungsdaten wird aber in einer Studie von Chan, Karceski, Lakonishok (2003, S. 671) in Frage gestellt. So lassen sich die teils erheblichen Unterschiede bezüglich der beobachtbaren Kurs-Gewinn-Quoten (KGV) von Aktiengesellschaften gut durch die historische Gewinnentwicklung der Unternehmen erklären – ein Prognosenutzen sei hingegen kaum nachweisbar.
siehe Fischer (2004, S. 91)
Siehe Deutsche Bundesbank (1999, S. 54), Eigermann (2001, S. 523) und Küting, Weber (2004, S. 423ff). Die Zielsetzung der vorgenannten Autoren besteht jedoch nicht in einer Korrektur der Jahresabschlussdaten, sondern in der Bewertung des „Bilanzierungsverhaltens“ des Unternehmens, das dann als eigenständiger Input im Rahmen des verwendeten Insolvenzprognoseverfahrens herangezogen wird.
siehe ULD (2006, S. 50)
Siehe Bemmann (2005, S. 57). Die durchschnittlichen jährlichen Insolvenzquoten der beiden genannten Unternehmensgruppen betragen im Zeitraum 1999–2003 3,6 % und 0,23 %.
Siehe Blum, Gleißner, Leibbrand (2005b). Siehe Fischer (2004, S. 97) für eine Auswahl von 150 Beispielen aus 18 Gruppen von weichen qualitativen Faktoren.
siehe Fischer (2004, S. 89)
siehe Basler Ausschuss (2000a, S. 17ff.) und Romeike, Wehrspohn (2004, S. 9)
siehe Bemmann (2005, S. 51ff.)
S&P (2003, S. 53). “Ratios are helpful in broadly defining a company’s position relative to rating categories. They are not intended to be hurdles or prerequisites that should be achieved to attain a specific debt rating. […].” und S&P (2003, S. 17) “There are no formulae for combining scores to arrive at a rating conclusion. Bear in mind that ratings represent an art as much as a science.”
siehe Blume, Lim, Mackinlay (1998) und Amato, Furfine (2004)
Siehe die über 100 Seiten umfassende Beschreibung der Elemente von Ratingprozessen bei Standard and Poors’s in S&P (2003).
Nach White (2001, S. 14) betragen die vom zu bewertenden Unternehmen zu tragenden „Listenpreise“ für die Erstellung eines Ratings durch Moody’s oder S&P 3,25 Basispunkte bei Anleihebeträgen von bis zu 500 Millionen US$ - bei einer Mindestgebühr von 25.000 US$ und einem Höchstbetrag von 125.000 US$ (S&P) bzw. 130.000 US$ (Moody’s). Für über 500 Mio. US$ hinausgehende Anleihebeträge berechnen beide Agenturen 2 Basispunkte. S&P kappt den Gesamtbetrag bei 200.000 US$, verlangt aber eine zusätzliche Gebühr von 25.000 US$ bei der erstmaligen Erstellung eines Ratings.
siehe Carey, Hrycay (2001), Altman, Rijken (2004) und Fons, Viswanathan (2004)
siehe Bemmann (2005, S. 6f.)
siehe Altman, Saunders (1998, S. 1737)
Die Kalibrierung eines Ratingsystems auf Basis empirischer Ausfalldaten wird beispielsweise in Sobehart et al. (2000, S. 23f.) und Stein (2002, S. 8ff.) beschrieben.
siehe Deutsche Bundesbank (1999)
siehe Bemmann (2005, S. 9ff. und die dort zitierte Literatur)
“There are no bad loans, only bad prices.”, siehe Falkenstein, Boral, Kocagil (2000, S. 5).
siehe Basler Ausschuss (2004, insb. Tz. 461f.)
siehe hierzu ausführlich Bemmann (2005, S. 32ff.)
siehe Bemmann (2005, S. 32ff.)
siehe Huschens, Höse (2003, S. 152f.) und Basler Ausschuss (2005, S. 31f.)
Die tatsächliche Relevanz dieses theoretischen Einwands ist noch umstritten. Es existieren empirische Hinweise darauf, dass die entsprechenden im Rahmen von Basel II unterstellten segmentspezifischen Korrelationsparameter um den Faktor 15 bis 120 (im Durchschnitt rund 50) zu hoch angesetzt werden, siehe hierzu Scheule (2003).
Blochwitz, Liebig, Nyberg (2000, S. 3): “It is usually much easier to recalibrate a more powerful model than to add statistical power to a calibrated model. For this reason, tests of power are more important in evaluating credit models than tests of calibration. This does not imply that calibration is not important, only that it is easier to carry out.”, analog Stein (2002, S. 9)
Für weitere Erläuterungen und Argumente für die Verwendung ordinaler Kenngrößen für die Gütebestimmung von Insolvenzprognosen siehe Bemmann (2005, S. 12ff.).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Dieser Artikel basiert wesentlich auf: Martin Bemmann, Verbesserung der Vergleichbarkeit von Schätzgüteergebnissen von Insolvenzprognosestudien, in: Dresden Discussion Paper Series in Economics. 08/2005; Martin Bemmann, Entwicklung und Validierung eines stochastischen Simulationsmodells für die Prognose von Unternehmensinsolvenzen, Dissertation, Technische Universität Dresden, TUDpress Verlag der Wissenschaften, Dresden, 2007

[Entwicklung-2] Zur Entwicklung der Insolvenzanzahl und -quoten sowie zum Bestand und zur Einbringbarkeit von Insolvenzforderungen siehe Statistisches Bundesamt (2004, S. 31 und S. 44), zu aktuellen Daten zum Insolvenzgeschehen siehe https://www.destatis.de/DE/ZahlenFakten/Indikatoren/LangeReihen/Insolvenzen/lrins01.html und https://www.destatis.de/DE/ZahlenFakten/Indikatoren/Konjunkturindikatoren/Insolvenzen/ins110.html (20. September 2012)

[3] Siehe Dimitras, Zanakis, Zoponidis (1996, S. 488) und Balcaen, Ooghe (2004, S. 4) oder Hartmann-Wendels et al. (2005, S. 4f.) für eine Analyse der Interessenten an Insolvenzprognoseverfahren für Unternehmen.

[4] siehe Franks, Servigny, Davydenko (2004, S. 4), Basler Ausschuss (2000b, S. 27f.), Basler Ausschuss (2000b, S. 7f.), Moody’s (2004, S. 13) und Gupton, Stein (2005).

[5] siehe Franks, Servigny, Davydenko, 2004, S. 13

[6] siehe English, Nelson (1998, S. 11f.), Treacy, Carey (2000, S. 897), Basler Ausschuss (2000a, S. 33), Escott, Glormann, Kocagil (2001a, S. 3) und Scheule (2003, S. 96ff.)

[7] siehe Fischer (2004, S. 13 und die dort zitierte Literatur)

[8] siehe Deutsche Bundesbank (2005, S. 44)

[9] siehe Basler Ausschuss (2004, §4), OeNB (2004b, S. 33)

[10] Siehe KfW (2005, S. 6): „Dies deutet auf die mittlerweile flächendeckende Verbreitung bankinterner Ratingtools hin, die nun auch bei kleinen Unternehmen Anwendung finden. […] Früher führten die für alle Kunden eines Kreditinstitutes weitgehend einheitlichen Zinssätze dazu, dass vor allem kleinere Unternehmen Schwierigkeiten hatten, überhaupt Kredite zu erhalten. Heute nutzen Banken und Sparkassen Ratingtools dazu, Kreditkonditionen zunehmend risikoorientiert zu gestalten. Damit wird insbesondere für kleine Unternehmen der Zugang zu Bankkrediten erleichtert.“

[11] siehe Basler Ausschuss (2000b, S. 109ff.), Altman, Saunders (1998, S. 1724), Keasey, Watson (1991, S. 90) oder Günther, Hübl, Niepel (2000, S. 347).

[12] siehe Frydman, Altman, Kao (1985, S. 270)

[13] siehe Bemmann (2007, S. 6)

[14] Die im Folgenden verwendete Terminologie wurde von Fischer (2004, S. 83) übernommen, der harte vs. weiche und quantitative vs. qualitative Daten abgrenzt. In der Insolvenzprognoseliteratur werden diese Begriffe meist synonym und deshalb häufig inkonsistent verwendet. Beispielsweise führt OeNB (2004a, S. 65) aus: „Qualitative Fragen unterliegen stets einem subjektiven Beurteilungsspielraum“, bezeichnet aber auch das zweifellos objektiv feststellbare „Heimatland des Schuldners“ als „qualitatives Ratingkriterium“, siehe OeNB (2004a, S. 66).

[15] Für Kennzahlen zur Quantifizierung des Kontoführungsverhaltens siehe Fritz, Hosemann (2000, S. 13ff.).

[16] Siehe bspw. McQuown (1993, S. 1f.). Gerade der Vorteil der „Vorwärtsgerichtetheit“ von Marktpreisen im Vergleich zu (historischen) Buchhaltungsdaten wird aber in einer Studie von Chan, Karceski, Lakonishok (2003, S. 671) in Frage gestellt. So lassen sich die teils erheblichen Unterschiede bezüglich der beobachtbaren Kurs-Gewinn-Quoten (KGV) von Aktiengesellschaften gut durch die historische Gewinnentwicklung der Unternehmen erklären – ein Prognosenutzen sei hingegen kaum nachweisbar.

[17] siehe Fischer (2004, S. 91)

[18] Siehe Deutsche Bundesbank (1999, S. 54), Eigermann (2001, S. 523) und Küting, Weber (2004, S. 423ff). Die Zielsetzung der vorgenannten Autoren besteht jedoch nicht in einer Korrektur der Jahresabschlussdaten, sondern in der Bewertung des „Bilanzierungsverhaltens“ des Unternehmens, das dann als eigenständiger Input im Rahmen des verwendeten Insolvenzprognoseverfahrens herangezogen wird.

[19] siehe ULD (2006, S. 50)

[20] Siehe Bemmann (2005, S. 57). Die durchschnittlichen jährlichen Insolvenzquoten der beiden genannten Unternehmensgruppen betragen im Zeitraum 1999–2003 3,6 % und 0,23 %.

[21] Siehe Blum, Gleißner, Leibbrand (2005b). Siehe Fischer (2004, S. 97) für eine Auswahl von 150 Beispielen aus 18 Gruppen von weichen qualitativen Faktoren.

[22] siehe Fischer (2004, S. 89)

[23] siehe Basler Ausschuss (2000a, S. 17ff.) und Romeike, Wehrspohn (2004, S. 9)

[24] siehe Bemmann (2005, S. 51ff.)

[25] S&P (2003, S. 53). “Ratios are helpful in broadly defining a company’s position relative to rating categories. They are not intended to be hurdles or prerequisites that should be achieved to attain a specific debt rating. […].” und S&P (2003, S. 17) “There are no formulae for combining scores to arrive at a rating conclusion. Bear in mind that ratings represent an art as much as a science.”

[26] siehe Blume, Lim, Mackinlay (1998) und Amato, Furfine (2004)

[27] Siehe die über 100 Seiten umfassende Beschreibung der Elemente von Ratingprozessen bei Standard and Poors’s in S&P (2003).

[28] Nach White (2001, S. 14) betragen die vom zu bewertenden Unternehmen zu tragenden „Listenpreise“ für die Erstellung eines Ratings durch Moody’s oder S&P 3,25 Basispunkte bei Anleihebeträgen von bis zu 500 Millionen US$ - bei einer Mindestgebühr von 25.000 US$ und einem Höchstbetrag von 125.000 US$ (S&P) bzw. 130.000 US$ (Moody’s). Für über 500 Mio. US$ hinausgehende Anleihebeträge berechnen beide Agenturen 2 Basispunkte. S&P kappt den Gesamtbetrag bei 200.000 US$, verlangt aber eine zusätzliche Gebühr von 25.000 US$ bei der erstmaligen Erstellung eines Ratings.

[29] siehe Carey, Hrycay (2001), Altman, Rijken (2004) und Fons, Viswanathan (2004)

[30] siehe Bemmann (2005, S. 6f.)

[31] siehe Altman, Saunders (1998, S. 1737)

[32] Die Kalibrierung eines Ratingsystems auf Basis empirischer Ausfalldaten wird beispielsweise in Sobehart et al. (2000, S. 23f.) und Stein (2002, S. 8ff.) beschrieben.

[33] siehe Deutsche Bundesbank (1999)

[34] siehe Bemmann (2005, S. 9ff. und die dort zitierte Literatur)

[35] “There are no bad loans, only bad prices.”, siehe Falkenstein, Boral, Kocagil (2000, S. 5).

[36] siehe Basler Ausschuss (2004, insb. Tz. 461f.)

[37] siehe hierzu ausführlich Bemmann (2005, S. 32ff.)

[38] siehe Bemmann (2005, S. 32ff.)

[39] siehe Huschens, Höse (2003, S. 152f.) und Basler Ausschuss (2005, S. 31f.)

[40] Die tatsächliche Relevanz dieses theoretischen Einwands ist noch umstritten. Es existieren empirische Hinweise darauf, dass die entsprechenden im Rahmen von Basel II unterstellten segmentspezifischen Korrelationsparameter um den Faktor 15 bis 120 (im Durchschnitt rund 50) zu hoch angesetzt werden, siehe hierzu Scheule (2003).

[41] Blochwitz, Liebig, Nyberg (2000, S. 3): “It is usually much easier to recalibrate a more powerful model than to add statistical power to a calibrated model. For this reason, tests of power are more important in evaluating credit models than tests of calibration. This does not imply that calibration is not important, only that it is easier to carry out.”, analog Stein (2002, S. 9)

[42] Für weitere Erläuterungen und Argumente für die Verwendung ordinaler Kenngrößen für die Gütebestimmung von Insolvenzprognosen siehe Bemmann (2005, S. 12ff.).