Entscheidungsbaum
Entscheidungsbäume (englisch: decision tree) sind geordnete, gerichtete Bäume, die der Darstellung von Entscheidungsregeln dienen. Die grafische Darstellung als Baumdiagramm veranschaulicht hierarchisch aufeinanderfolgende Entscheidungen. Sie haben eine Bedeutung in zahlreichen Bereichen, in denen automatisch klassifiziert wird oder aus Erfahrungswissen formale Regeln hergeleitet oder dargestellt werden.
Eigenschaften und Einsatz
Entscheidungsbäume sind eine Methode zur automatischen Klassifikation von Datenobjekten und damit zur Lösung von Entscheidungsproblemen. Sie werden außerdem zur übersichtlichen Darstellung von formalen Regeln genutzt. Ein Entscheidungsbaum besteht immer aus einem Wurzelknoten und beliebig vielen inneren Knoten sowie mindestens zwei Blättern. Dabei repräsentiert jeder Knoten eine logische Regel und jedes Blatt eine Antwort auf das Entscheidungsproblem.
Die Komplexität und Semantik der Regeln sind von vornherein nicht beschränkt. Bei binären Entscheidungsbäumen kann jeder Regelausdruck nur einen von zwei Werten annehmen. Alle Entscheidungsbäume lassen sich in binäre Entscheidungsbäume überführen.
Entscheidungsbäume kommen in zahlreichen Bereichen zum Einsatz, z. B.
- in der Stochastik als Wahrscheinlichkeitsbaum zur Veranschaulichung bedingter Wahrscheinlichkeiten (z. B. bei absoluten Häufigkeiten)
- im Maschinellen Lernen als Methode zur automatischen Klassifikation von Objekten
- im Data-Mining
- in der Entscheidungstheorie
- in der ärztlichen Entscheidungsfindung (Medizin) und in der Notfallmedizin
- in Business-Rule-Management-Systemen (BRMS) für die Definition von Regeln
Funktionsweise
Klassifizieren mit Entscheidungsbäumen
Um eine Klassifikation eines einzelnen Datenobjektes abzulesen, geht man vom Wurzelknoten entlang des Baumes abwärts. Bei jedem Knoten wird ein Attribut abgefragt und eine Entscheidung über die Auswahl des folgenden Knoten getroffen. Diese Prozedur wird so lange fortgesetzt, bis man ein Blatt erreicht. Das Blatt entspricht der Klassifikation. Ein Baum enthält grundsätzlich Regeln zur Beantwortung von nur genau einer Fragestellung.
Beispiel: Ein Entscheidungsbaum mit geringer Komplexität
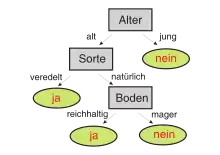
Der nebenstehende binäre Entscheidungsbaum gibt eine Antwort auf die Frage, ob ein Apfelbaum Früchte tragen wird. Als Eingabe benötigt der Baum einen Vektor mit Angaben zu den Attributen eines Apfelbaumes. Ein Apfelbaum kann beispielsweise die Attribute alt, natürliche Sorte und reichhaltiger Boden besitzen. Beginnend mit dem Wurzelknoten werden nun die Entscheidungsregeln des Baumes auf den Eingabevektor angewendet. Dabei wird im Beispielbaum an jedem Knoten ein Attribut des Eingabevektors abgefragt, am Wurzelknoten etwa das Alter des Apfelbaumes. Die Antwort entscheidet über den Folgeknoten und damit über die nächste anzuwendende Entscheidungsregel, in diesem Falle die Frage zur Sorte, und danach die Frage nach der Bodenbeschaffenheit. Gelangt man nach einer Folge ausgewerteter Regeln an ein Blatt, erhält man die Antwort auf die ursprüngliche Frage. Nicht immer müssen alle Ebenen des Entscheidungsbaums durchlaufen werden. Für den oben beschriebenen Apfelbaum ist die Antwort ja, also dass der Baum Früchte tragen wird. Diesen Entscheidungsvorgang nennt man formal Klassifikation.
Induktion von Entscheidungsbäumen
Entscheidungsbäume können entweder von Experten manuell aufgeschrieben werden oder mit Techniken des maschinellen Lernens automatisch aus gesammelten Erfahrungswerten induziert werden. Hierzu gibt es mehrere konkurrierende Algorithmen.
Die Induktion der Entscheidungsbäume erfolgt üblicherweise rekursiv im Top-down-Prinzip. Dazu ist es von entscheidender Bedeutung, dass ein geeigneter Datensatz mit verlässlichen Erfahrungswerten zum Entscheidungsproblem (der sogenannte Trainingsdatensatz) vorliegt. Das bedeutet, dass zu jedem Objekt des Trainingsdatensatzes die Klassifikation des Zielattributs bekannt sein muss. Bei jedem Induktionsschritt wird nun das Attribut gesucht, mit welchem sich die Trainingsdaten in diesem Schritt bezüglich des Zielattributs am besten klassifizieren lassen. Als Maß für die Bestimmung der besten Klassifizierung kommen Entropie-Maße, Gini-Index oder andere zur Anwendung. Das ermittelte Attribut wird nun zur Aufteilung der Daten verwendet. Auf die so entstandenen Teilmengen wird die Prozedur rekursiv angewendet, bis in jeder Teilmenge nur noch Objekte mit einer Klassifikation enthalten sind. Am Ende ist ein Entscheidungsbaum entstanden, der das Erfahrungswissen des Trainingsdatensatzes in formalen Regeln beschreibt.
Die Bäume können nun zum automatischen Klassifizieren anderer Datensätze oder zum Interpretieren und Auswerten des entstandenen Regelwerks genutzt werden.
Algorithmen im Vergleich
Die Algorithmen zur automatischen Induktion von Entscheidungsbäumen setzen alle auf dem gleichen rekursiven Top-down-Prinzip auf. Sie unterscheiden sich nur in ihren Kriterien zur Auswahl der Attribute und Werte der Regeln an den Knoten des Baumes, in ihren Kriterien zum Abbruch des Induktionsprozesses und in möglichen Nachbearbeitungsschritten, die einen bereits berechneten Ast eines Baumes (oder ganze Bäume) nachträglich anhand diverser Kriterien optimieren.
Die Praxis unterscheidet verschiedene Familien von Algorithmen:
- Die älteste Familie sind die CHAIDs (Chi-square Automatic Interaction Detectors) von 1964.[1] Sie können Bäume auf Basis von diskreten Attributen erzeugen.
- Die Familie der CARTs (Classification And Regression Trees) erweitert die CHAIDS vor allem um die Möglichkeit, reellwertige Attribute verarbeiten zu können, indem ein Teilungs-Kriterium (englisch split-criterion) zur Aufteilung reellwertiger Attribute in diskrete Kategorien genutzt wird. Zudem werden einige Optimierungsstrategien wie z. B. das Pruning eingeführt.
- Die jüngsten Algorithmen sind der ID3-Algorithmus[2] und seine Nachfolger C4.5 und C5.0[3]. Sie zählen formal zur Familie der CARTs, werden aber häufig als eigenständige Gruppe gesehen, da sie im Vergleich zu CART zahlreiche neue Optimierungsstrategien einführen.
Fehlerrate und Wirksamkeit
Die Fehlerrate eines Entscheidungsbaumes ist die Anzahl der inkorrekt klassifizierten Datenobjekte im Verhältnis zu allen Datenobjekten eines Datensatzes. Diese Zahl wird regelmäßig entweder auf den benutzten Trainingsdaten oder besser auf einer zu den Trainingsdaten disjunkten Menge an möglichst korrekt klassifizierten Datenobjekten ermittelt.
Je nach Anwendungsbereich kann es von besonderer Bedeutung sein, entweder die Anzahl der falsch positiv oder falsch negativ klassifizierten Objekte im Speziellen niedrig zu halten. So ist es etwa in der Notfallmedizin wesentlich unschädlicher einen gesunden Patienten zu behandeln, als einen kranken Patienten nicht zu behandeln. Die Wirksamkeit von Entscheidungsbäumen ist daher immer auch eine kontextabhängige Größe.
Darstellung in disjunktiver Normalform
Jede mögliche Klassifikation eines Entscheidungsbaumes lässt sich in Disjunktiver Normalform angeben. Hierzu betrachtet man alle Blätter dieser Klassifikation und deren Pfade zum Wurzelknoten. Für jeden dieser Pfade werden alle Bedingungen der Entscheidungsknoten entlang des Pfades miteinander in Konjunktion gesetzt und die dadurch entstehenden Terme in Disjunktion gesetzt. Für das oben abgebildete Beispiel ergibt sich für die Klassifikation „Apfelbaum trägt Früchte“ (ja) folgende Aussage:
Vorteile
Interpretierbarkeit und Verständlichkeit
Ein großer Vorteil von Entscheidungsbäumen ist, dass sie gut erklärbar und nachvollziehbar sind. Dies erlaubt dem Benutzer, das Ergebnis auszuwerten und Schlüsselattribute zu erkennen. Das ist vor allem nützlich, wenn grundlegende Eigenschaften der Daten von vornherein nicht bekannt sind. Damit ist die Induktion von Entscheidungsbäumen auch eine wichtige Technik des Data-Minings.
Entscheidungsbäume können verständliche Regeln generieren. Sie führen eine Klassifizierung durch, ohne dass viel Berechnung erforderlich ist. Sie können sowohl kontinuierliche als auch kategoriale Variablen verarbeiten. Sie geben einen klaren Hinweis darauf, welche Felder für die Vorhersage oder Klassifizierung am wichtigsten sind.[4]
Wird jedoch Boosting oder Bagging eingesetzt, sind Entscheidungsbaummodelle auch schwer nachvollziehbar.
Nachteile
Klassifikationsgüte in reellwertigen Datenräumen
Ein oft benannter Nachteil der Entscheidungsbäume ist die relativ geringe Klassifikationsgüte in reellwertigen Datenräumen, wenn man die Bäume zur automatischen Klassifikation einsetzt. So schneiden die Bäume aufgrund ihres diskreten Regelwerks bei den meisten Klassifikationsproblemen aus der realen Welt im Vergleich zu anderen Klassifikationstechniken wie beispielsweise Künstlichen Neuronalen Netzen oder Support-Vektor-Maschinen etwas schlechter ab.[5][6] Das bedeutet, dass durch die Bäume zwar für Menschen leicht nachvollziehbare Regeln erzeugt werden können, diese verständlichen Regeln aber für Klassifikationsprobleme der realen Welt statistisch betrachtet oft nicht die bestmögliche Qualität besitzen.[7][8]
Größe der Entscheidungsbäume und Überanpassung
Ein weiterer Nachteil ist die mögliche Größe der Entscheidungsbäume, wenn sich aus den Trainingsdaten keine einfachen Regeln induzieren lassen. Dies kann sich mehrfach negativ auswirken: Zum einen verliert ein menschlicher Betrachter schnell den Gesamtüberblick über den Zusammenhang der vielen Regeln, zum anderen führen solche großen Bäume aber auch meistens zur Überanpassung an den Trainingsdatensatz, so dass neue Datensätze nur fehlerhaft automatisch klassifiziert werden. Es wurden deshalb sogenannte Pruning-Methoden entwickelt, welche die Entscheidungsbäume auf eine vernünftige Größe kürzen. Beispielsweise kann man die maximale Tiefe der Bäume beschränken oder eine Mindestanzahl der Objekte pro Knoten festlegen.
Weiterverarbeitung der Ergebnisse
Oft bedient man sich der Entscheidungsbäume nur als Zwischenschritt zu einer effizienteren Darstellung des Regelwerkes. Um zu den Regeln zu gelangen, werden durch verschiedene Verfahren unterschiedliche Entscheidungsbäume generiert. Dabei werden häufig auftretende Regeln extrahiert. Die Optimierungen werden überlagert, um einen robusten, allgemeinen und korrekten Regelsatz zu erhalten. Dass die Regeln in keinerlei Beziehungen zueinander stehen und dass widersprüchliche Regeln erzeugt werden können, wirkt sich nachteilig auf diese Methode aus.
Schätzaufgaben und Klassifizierungsprobleme
Entscheidungsbäume eignen sich weniger für Schätzaufgaben, bei denen das Ziel darin besteht, den Wert eines kontinuierlichen Attributs vorherzusagen. Entscheidungsbäume sind bei vielen Klassen und einer relativ geringen Anzahl von Trainingsbeispielen fehleranfällig bei Klassifizierungsproblemen.
Hoher Rechenaufwand
Das Trainieren eines Entscheidungsbaums kann rechenintensiv sein. Das Wachstum eines Entscheidungsbaums ist rechenintensiv. An jedem Knoten muss jedes Kandidaten-Aufteilungsfeld sortiert werden, bevor die beste Aufteilung gefunden werden kann. In einigen Algorithmen werden Feldkombinationen verwendet, und es muss nach optimalen Kombinationsgewichten gesucht werden. Bereinigungsalgorithmen können auch teuer sein, da viele Kandidaten-Teilbäume gebildet und verglichen werden müssen.[4]
Weiterentwicklungen und Erweiterungen
Entscheidungswälder
Eine Methode, um die Klassifikationsgüte beim Einsatz von Entscheidungsbäumen zu steigern, ist der Einsatz von Mengen von Entscheidungsbäumen anstelle von einzelnen Bäumen.[9] Solche Mengen von Entscheidungsbäumen werden als Entscheidungswälder (englisch: decision forests) bezeichnet.[10]
Der Gebrauch von Entscheidungswäldern zählt im maschinellen Lernen zu den sogenannten Ensemble-Techniken. Die Idee der Entscheidungswälder ist, dass ein einzelner Entscheidungsbaum zwar keine optimale Klassifikation liefern muss, die Mehrheitsentscheidung einer Menge von geeigneten Bäumen dies aber sehr wohl leisten kann.[11] Verbreitete Methoden zur Erzeugung geeigneter Wälder sind Boosting,[12] Bagging[13] und Arcing.
Nachteil der Entscheidungswälder ist, dass es für Menschen nicht mehr so einfach ist, die in allen Bäumen enthaltenen Regeln in ihrer Gesamtheit in einfacher Weise zu interpretieren, so wie es bei einzelnen Bäumen möglich wäre.[14]
Kombination mit Neuronalen Netzen
Entscheidungsbäume können mit neuronalen Netzen kombiniert werden. So ist es möglich, ineffiziente Äste des Baumes durch neuronale Netze zu ersetzen, um eine höhere, allein mit den Bäumen nicht erreichbare Klassifikationsgüte zu erreichen.[15] Auch können die Vorteile beider Klassifikationsmethoden durch die Abbildung von Teilstrukturen in die jeweils andere Methodik genutzt werden: Die Bäume brauchen nicht so viele Trainingsdaten zur Induktion wie die neuronalen Netze. Dafür können sie ziemlich ungenau sein, besonders wenn sie klein sind. Die Neuronalen Netze hingegen klassifizieren genauer, benötigen aber mehr Trainingsdaten. Deshalb versucht man, die Eigenschaften der Entscheidungsbäume zur Generierung von Teilen neuronaler Netze zu nutzen, indem sogenannte TBNN (Tree-Based Neural Network) die Regeln der Entscheidungsbäume in die neuronalen Netze übersetzen.
Praktische Anwendungen
Anwendungsprogramme
Es gibt etliche Anwendungsprogramme, die Entscheidungsbäume implementiert haben, so werden sie zum Beispiel in den Statistiksoftwarepaketen GNU R, Scikit-learn[16] (XGBoost), SPSS und SAS angeboten. Die letzteren beiden Pakete verwenden – wie die meisten anderen Data-Mining-Software-Pakete auch – den CHAID-Algorithmus.
Beispiel: Kundenklassifikation
Eine Bank möchte mit einer Direct-Mailing-Aktion einen neuen Service verkaufen. Um die Erfolgsaussichten zu erhöhen, sollen mit der Aktion nur Haushalte angesprochen werden, die einer Kombination von demografischen Variablen entsprechen, die ein entsprechender Entscheidungsbaum als optimal erklärt hat. Dieser Prozess wird Data Segmentation oder auch Segmentation Modeling genannt.
Siehe auch
Literatur
- Leo Breiman, Jerome H. Friedman, Richard A. Olshen, Charles J. Stone: Classification and regression trees, Wadsworth International Group, Belmont CA, 1984, ISBN 0-412-04841-8
- Tom M. Mitchell: Machine Learning, McGraw-Hill, Boston USA, 1997, ISBN 0-07-115467-1
- Jiawei Han, Micheline Kamber: Data Mining, Morgan Kaufmann publishers, San Francisco CA, 2006 (2nd edition), ISBN 978-1558609013
- Peter Dörsam: Entscheidungstheorie anschaulich dargestellt, Pd-Verlag, Heidenau, 2007 (5. Auflage), ISBN 978-3867073059
- Günter Bamberg, Adolf G. Coenenberg, Michael Krapp: Betriebswirtschaftliche Entscheidungslehre, Verlag Franz Vahlen, München, 2008 (14. Auflage), ISBN 978-3-8006-3506-1
Weblinks
Einzelnachweise
- J.A. Sonquist, J.N. Morgan: The Detection of Interaction Effects, Survey Research Center, Institute for Social Research, University of Michigan, Ann Arbor.
- J.R. Quinlan: Induction of decision trees, Machine learning, 1(1):81-106, 1986
- Xindong Wu, Vipin Kumar, J. Ross Quinlan, Joydeep Ghosh, Qiang Yang, Hiroshi Motoda, Geoffrey J. McLachlan, Angus Ng, Bing Liu and Philip S. Yu, et al.: Top 10 algorithms in data mining, Knowledge and Information Systems Volume 14, Number 1 (2008), 1-37
- GeeksforGeeks: Decision Tree
- R.King, C.Feng, A.Sutherland: Comparison of classification algorithms on large real-world problems, Applied Artificial Intelligence, 9(3):259-287, Mai/Juni 1995
- O.Gascuel, B.Bouchon-Meunier, G.Caraux, P.Gallinari, A. Guénoche, Y.Guermeur: Twelve numerical, symbolic and hybrid supervised classification methods, International Journal of Pattern Recognition and Artificial Intelligence, 12(5):517-571, 1998
- A.Flöter: Analyzing biological expression data based on decision tree induction, Dissertation, Universität Potsdam, 2006
- M.Murata, Q.Ma, H.Isahara: Comparison of three machine-learning methods for thai part-of-speech tagging, ACM Transaction on Asian Language Information Processing, 1(2):145-158, Juni 2002
- Y.Freund: Boosting a weak learning algorithm by majority, Information and Computation, 121(2):256-285, 1995
- W.Tong, Q.Xie, H.Hong, H.Fang, L.Shi, R.Perkins, E.F.Petricoin: Using decision forests to classify prostate cancer samples on the basis of seldi-tof ms data: Assessing chance correlation and prediction confidence, Environmental Health Perspectives, 112(16):1622-1627, 2004
- E.Bauer, R.Kohavi: An empirical comparison of voting classification algorithms: Bagging, Boosting, and variants, Machine Learning, 36(1-2):105-139, 1998
- R.E.Schapire: A short introduction to boosting, Japanese Society for Artificial Intelligence, 14(5):771-780, 1999
- L.Breiman: Bagging predictors, Machine Learning, 24(2):123-140, 1996
- R.Nock: Inducing interpretable voting classifiers without trading accuracy for simplicity: Theoretical results, approximation algorithms, and experiments, Journal of Artificial Intelligence Research, 17:137-170, August 2002
- A.K. Seewald, J. Petrak, G. Widmer: Hybrid decision tree learners with alternative leaf classifiers, Proceedings of the 14th International FLAIRS conference, AAAI Press, Menlo Park CA, 2000
- Decision Trees — scikit-learn documentation. Abgerufen am 24. August 2018.