Schätzgütemaße für kategoriale Insolvenzprognosen

Schätzgütemaße für kategoriale Insolvenzprognosen messen die Qualität kategorialer Insolvenzprognosen. Als kategoriale Insolvenzprognosen werden Insolvenzprognosen bezeichnet, die lediglich zwei mögliche Ausprägungen zur Beurteilung der gerateten Unternehmen kennen: „Unternehmen A wird voraussichtlich (innerhalb des nächsten Jahres) ausfallen“ vs. „Unternehmen B wird voraussichtlich (innerhalb des nächsten Jahres) nicht ausfallen“.[1]

Arten von Prognosefehlern

Kontingenztabelle

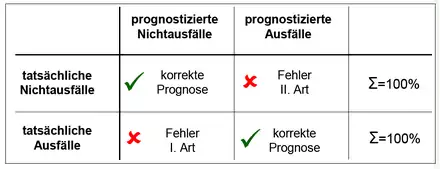
Kategoriale Insolvenzprognosen teilen die zu beurteilenden Unternehmen in zwei Gruppen, „voraussichtlich insolvent“ vs. „voraussichtlich nicht insolvent“ ein. Keines der heute verwendeten Insolvenzprognoseverfahren ist jedoch auch nur annähernd in der Lage, derart trennscharfe und gleichzeitig stets korrekte Prognosen zu erstellen.[2] Abgesehen von „Zufallstreffern“ in kleinen Stichproben, werden kategoriale Insolvenzprognosen deshalb stets Fehler aufweisen. Hierbei gibt es zwei mögliche Fehlerarten: Fehler des Typs I – tatsächliche Ausfälle, die als Nicht-Ausfälle prognostiziert wurden (auch Fehler 1. Art, α-Fehler, false negative proportion) – und Fehler des Typs II – tatsächliche Nicht-Ausfälle, die als Ausfälle prognostiziert wurden (auch Fehler 2. Art, β-Fehler, false positive proportion). Üblich ist es, Fehler des Typs I ins Verhältnis zu allen tatsächlichen Ausfällen und Fehler des Typs II ins Verhältnis zu allen tatsächlichen Nicht-Ausfällen zu setzen (siehe die folgende Abbildung).

In der Insolvenzprognoseliteratur werden die Terme 100 % – Fehler 1. Art auch als Trefferquote (hit rate, true positive proportion) und Fehler 2. Art auch als Fehlalarmquote (false alarm rate) bezeichnet.[3][4]

Klassifizierungsfehler in Abhängigkeit vom gewählten Schwellenwert und den Scoredichtefunktionen für insolvente und nichtinsolvente Unternehmen

Als Gütemaße können beispielsweise der ungewichtete Mittelwert[5] beider Fehlerquoten oder aber ein gewichteter Mittelwert, wobei als Gewichtungsfaktoren beispielsweise die Anteile der Ausfaller und Nichtausfaller an allen Unternehmen des Samples verwendet werden können („Bayesscher Gesamtfehler“[6]) oder aber die Kosten[7], die mit beiden Fehlerarten verbunden sind (Fehler-Typ I: Kreditausfallkosten, Fehler-Typ II: entgangene Kreditmarge, sonstiges „Cross-Selling-Geschäft“[8]).

Des Weiteren besteht bei allen Verfahren, die kategoriale Insolvenzprognosen erstellen, ein Zielkonflikt zwischen Fehlern I und II. Art. Je nach Parametrisierung des Insolvenzprognoseverfahrens kann erreicht werden, dass 0 % aller Ausfälle und 100 % aller Nichtausfälle – oder umgekehrt – richtig erkannt werden, und auch eine Feinjustierung zwischen diesen Extrempunkten ist in der Regel möglich (siehe die Abbildung unten[9]).[10] Angesichts der unendlich vielen alternativen Möglichkeiten ist die Wahl einer konkreten Fehler-I-II-Kombination demnach willkürlich und kann somit nur bedingt geeignet sein, die Qualität eines Verfahrens zu messen.

Eine denkbare Rechtfertigung für die Beschränkung auf eine einzige Fehler-I-II-Kombination bei der Beurteilung der Schätzgüte eines Verfahrens wäre die Verwendung von „optimalen“ („kostenminimalen“) Fehlerkombination I. und II. Art. Welche Fehler-I-II-Kombination jedoch „optimal“ ist, ist subjektiv verschieden – bei einer Bank sind die Kosten für einen Fehler I. Art im Verhältnis zu einem Fehler II. Art vermutlich wesentlich höher als bei einem Lieferanten des Unternehmens – ist von subjektiv beeinflussbaren Nebenbedingungen abhängig (beispielsweise den konkreten Ausgestaltungen von Kreditkonditionen wie Zinssätzen, Sicherheiten, Bürgschaften, ...) und ist von im Zeitverlauf veränderlichen Größen abhängig, beispielsweise von der durchschnittlichen Ausfallquote.[11]

Umrechnung kategorialer in ordinale Schätzgütemaße

Moderne Insolvenzprognoseverfahren basieren nicht mehr auf kategorialen, sondern auf ordinalen oder kardinalen Insolvenzprognosen. Speziell für ordinale Insolvenzprognosen existieren mittlerweile etablierte Schätzgütemaße. Ordinale Schätzgütemaße bewerten dabei die Klassifikationsleistung eines Insolvenzprognoseverfahrens nicht anhand einer einzigen, willkürlich bestimmten, Fehler-I-II-Kombination, sondern anhand der Gesamtheit aller möglichen mit dem Prognoseverfahren erzeugbaren Fehler-I-II-Kombinationen. Unter empirisch gut bewährten Annahmen lässt sich die ordinale Schätzgüte eines Verfahrens anhand einer einzigen Fehler-I-II-Kombination wie folgt abschätzen[12]:

$AR^{*}=0,5\cdot {\frac {\ln {F_{II}}-\ln {(1-F_{I})}}{\ln {F_{II}}+\ln {(1-F_{I})}}}+0,5\cdot {\frac {\ln {F_{I}}-\ln {(1-F_{II})}}{\ln {F_{I}}+\ln {(1-F_{II})}}}$

mit AR^* ... Accuracy Ratio,

F_I ... Fehler I. Art,

F_II ... Fehler II. Art

Quellen

Bemmann (2005).
Siehe hierzu beispielsweise die Übersichten in Bemmann (2005, S. 73ff.)
Siehe beispielsweise Swets (1973, S. 995), Engelmann, Hayden, Tasche (2003, S. 13) und OeNB (2004c, S. 21).
Eine alternative, möglicherweise intuitivere Definition von Trefferquote wäre: Anteil der tatsächlich insolventen Unternehmen an allen Unternehmen, die vom Prognoseverfahren als insolvent prognostiziert wurden. Eine alternative, möglicherweise intuitivere Definition von Fehlalarmquote wäre: Anteil aller „Fehlalarme“ (nichtinsolvente Unternehmen, die als insolvent prognostiziert wurden) an allen „Alarmen“ (Prognosen, die einen Ausfall des Unternehmens behaupten). Für eine Übersicht weiterer kategorialer Kennzahlen siehe Swets, Dawes, Monahan (2000, S. 25f.) und Swets, Pickets (1982, S. 24ff.).
siehe Balcaen, Ooghe (2004, S. 12 und die dort zitierte Literatur)
Der „bayessche Gesamtfehler“ gibt an, welcher Anteil der Prognosen falsch ist, ohne dabei zwischen Fehler I. und II. Art zu unterscheiden. Für die Beurteilung der Güte von Insolvenzprognosen ist diese Kenngröße denkbar ungeeignet, da sich bereits mit der naiven Prognose „kein Unternehmen wird je insolvent“ Prognosen abgeben lassen, deren Gesamtfehler nahe bei 0 % (in Höhe der durchschnittlichen Insolvenzrate) liegt und damit selbst sehr trennfähige Insolvenzprognosen schlägt, selbst wenn diese nur einen niedrigen Fehler II. Art aufweisen, siehe OeNB (2004a, S. 117ff.).
siehe beispielsweise Nanda, Pendharkar (2001, S. 155ff.)
siehe beispielsweise OeNB (2004b, S. 33, 80)
Abbildung in Anlehnung an Deutsche Bundesbank (2003a, S. 73), Engelmann, Hayden, Tasche (2003, S. 5) und OeNB (2004a, S. 107).
siehe Ohlson (1980, S. 124ff.)
siehe Balcaen, Ooghe (2004, S. 15)
siehe Bemmann (2005, S. 27)

Literatur

Balcaen, S., Ooghe, H. (2004): "35 Years of Studies on Business Failure: An Overview of the Classic Statistical Methodologies and their Related Problems", Vlerick Leuven Gent Working Paper Series 2004/15, 2004, auch erschienen in British Accounting Review, Bd. 38 (1), S. 63–93

Bemmann, M. (2005): "Verbesserung der Vergleichbarkeit von Schätzgüteergebnissen von Insolvenzprognosestudien", in Dresden Discussion Paper Series in Economics 08/2005

Deutsche Bundesbank (Hrsg.) (2003a): "Validierungsansätze für interne Ratingsysteme", in Monatsbericht September 2003, S. 61–74

Engelmann, B., Hayden, E., Tasche, D. (2003): "Measuring the Discriminative Power of Rating Systems", Deutsche Bundesbank, Discussion Paper, Series 2: Banking and Financial supervision

Nanda, S., Pendharkar, P. (2001): "Linear Models for Minimizing Misclassification Costs in Bankruptcy Prediction", in International Journal of Intelligent Systems in Accounting, Finance and Management, Bd. 10, S. 155–168

Österreichische Nationalbank (Hrsg.)(2004a): "Ratingmodelle und -validierung" (PDF; 2,3 MB), Leitfadenreihe zum Kreditrisiko, Wien

Österreichische Nationalbank (Hrsg.)(2004b): "Kreditvergabeprozess und Kreditrisikomanagement" (PDF; 3,5 MB), Leitfadenreihe zum Kreditrisiko, Wien

Österreichische Nationalbank (Hrsg.)(2004c): "Neue quantitative Modelle der Bankenaufsicht" (PDF; 1,3 MB), Leitfadenreihe zum Kreditrisiko, Wien

Ohlson, J.A. (1980): "Financial Ratios and the Probabilistic Prediction of Bankruptcy", in Journal of Accounting Research, Bd. 18 (1), S. 109–131

Swets, J. A. (1973): "The Relative Operating Characteristic in Psychology", in Science, Bd. 182, S. 990–1.000

Swets, J. A., Picket, R. M. (1982): "Evaluation of Diagnostic Systems, Methods from Signal Detection Theory", Academic Press, series in cognition and perception, New York et al.

Swets, J.A., Dawes, R.M., Monahan, J. (2000): "Psychological Science Can Improve Diagnostic Decisions", in Psychological Science in the Public Interest, Bd. 1 (1), S. 1–26

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Bemmann (2005).

[2] Siehe hierzu beispielsweise die Übersichten in Bemmann (2005, S. 73ff.)

[3] Siehe beispielsweise Swets (1973, S. 995), Engelmann, Hayden, Tasche (2003, S. 13) und OeNB (2004c, S. 21).

[4] Eine alternative, möglicherweise intuitivere Definition von Trefferquote wäre: Anteil der tatsächlich insolventen Unternehmen an allen Unternehmen, die vom Prognoseverfahren als insolvent prognostiziert wurden. Eine alternative, möglicherweise intuitivere Definition von Fehlalarmquote wäre: Anteil aller „Fehlalarme“ (nichtinsolvente Unternehmen, die als insolvent prognostiziert wurden) an allen „Alarmen“ (Prognosen, die einen Ausfall des Unternehmens behaupten). Für eine Übersicht weiterer kategorialer Kennzahlen siehe Swets, Dawes, Monahan (2000, S. 25f.) und Swets, Pickets (1982, S. 24ff.).

[5] siehe Balcaen, Ooghe (2004, S. 12 und die dort zitierte Literatur)

[6] Der „bayessche Gesamtfehler“ gibt an, welcher Anteil der Prognosen falsch ist, ohne dabei zwischen Fehler I. und II. Art zu unterscheiden. Für die Beurteilung der Güte von Insolvenzprognosen ist diese Kenngröße denkbar ungeeignet, da sich bereits mit der naiven Prognose „kein Unternehmen wird je insolvent“ Prognosen abgeben lassen, deren Gesamtfehler nahe bei 0 % (in Höhe der durchschnittlichen Insolvenzrate) liegt und damit selbst sehr trennfähige Insolvenzprognosen schlägt, selbst wenn diese nur einen niedrigen Fehler II. Art aufweisen, siehe OeNB (2004a, S. 117ff.).

[7] siehe beispielsweise Nanda, Pendharkar (2001, S. 155ff.)

[8] siehe beispielsweise OeNB (2004b, S. 33, 80)

[9] Abbildung in Anlehnung an Deutsche Bundesbank (2003a, S. 73), Engelmann, Hayden, Tasche (2003, S. 5) und OeNB (2004a, S. 107).

[10] siehe Ohlson (1980, S. 124ff.)

[11] siehe Balcaen, Ooghe (2004, S. 15)

[12] siehe Bemmann (2005, S. 27)