Ameisenalgorithmus

Ameisenalgorithmen gehören zu den Metaheuristiken für Verfahren der kombinatorischen Optimierung, die auf dem modellhaften Verhalten von realen Ameisen bei der Futtersuche basieren. Die meisten Ameisenalgorithmen erfüllen auch die von Marco Dorigo vorgestellte ACO (Ant Colony Optimization)-Metaheuristik.

Bestimmte Verhaltensmuster der Ameisen bilden die Grundlage für Optimierungs-Algorithmen (hier Dorylus).

Natürliches Vorbild

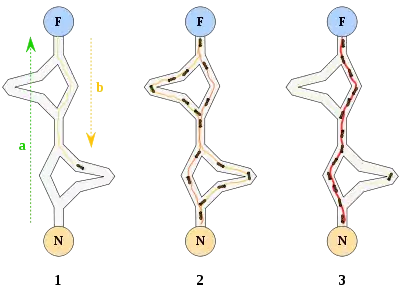
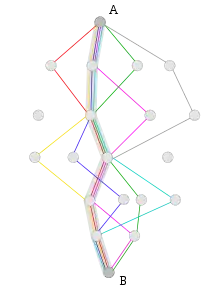
1: Die erste Ameise findet eine Futterquelle (F), benutzt den Weg (a), dann erreicht sie das Nest (N), und hinterlässt eine Pheromonspur. 2: Andere Ameisen folgen der ersten auf 4 möglichen Pfaden. 3: Die Ameisen folgen dem kürzesten Pfad.

Bestimmtes Verhalten von Ameisen wurde zur Formulierung von Optimierungs-Algorithmen verwendet. Hier wird mit einem Ameisenkolonie-Algorithmus (ACS) der kürzeste Weg in einem Graphen zwischen zwei Punkten A und B, gesucht.

Bei der Futtersuche scheiden einzelne Ameisen entlang ihres Weges einen Duftstoff (Pheromon) aus. Andere Ameisen wählen wahrscheinlicher einen Weg mit höherer Pheromonkonzentration. Verbindet man in einem Experiment eine Futterquelle mit zwei unterschiedlich langen Wegen mit dem Nest, so betreten die Ameisen auf ihrer Suche nach Futter beide Wege etwa gleich häufig. Die Ameisen auf dem kürzeren Weg kehren jedoch schneller von der Futterstelle zurück, so dass mit der Zeit auf dem kürzesten Pfad eine höhere Pheromonkonzentration als auf dem anderen vorherrscht. In der Folge wählen die nachkommenden Ameisen bevorzugt diesen Weg: Sie scheinen entlang einer Straße zu laufen, eine Ameisenstraße ist entstanden.

Diese Art von Ameisenoptimierung wurde schon in den 1940er Jahren vom späteren Physik-Nobelpreisträger Richard P. Feynman beobachtet und in seinem populären Buch Surely you are joking, Mr. Feynman anschaulich beschrieben.[1]

Übertragung auf Algorithmen

Dieses Vorgehen lässt sich als Schwarmintelligenz beschreiben: eine höhere Leistung (hier als Beispiel die Lösung eines Optimierungsproblems, nämlich die Suche nach der kürzesten Route) wird durch das Zusammenspiel von vielen einfachen Akteuren erbracht, die jeweils nur einen Teil zur Gesamtlösung beisteuern können. Deswegen kann man Ameisenalgorithmen auch den Agentenbasierten Modellen zuordnen.

Der erste Ameisenalgorithmus, genannt Ant System (AS), wurde vom italienischen Wissenschaftler Marco Dorigo vorgestellt (1991, 1996). Er wandte AS auf das bekannte informatische Problem des Handlungsreisenden an, da eine Übertragung von der Suche nach kürzesten Wegen auf dieses Problem naheliegend ist.

Wichtige Erweiterungen und Modifikationen lieferten in den Folgejahren Luca Maria Gamberdella mit Ant Colony System (ACS, 1997) und Thomas Stützle mit Max-Min Ant System (MMAS, 1999), mit dem bisher die besten Ergebnisse für das Problem des Handlungsreisenden erzielt wurden.

Mit Ameisenalgorithmen lassen sich vor allem kombinatorische Optimierungsprobleme lösen, beispielsweise Projektplanungsprobleme oder das Quadratische Zuordnungsproblem, IP-Routing oder Probleme der Logistik. Da es sich um heuristische Optimierungsverfahren handelt, kann nicht garantiert werden, dass immer die optimale Lösung gefunden wird. Deshalb ist ein Einsatz auch nur dann sinnvoll, wenn eine optimale Lösung nicht unbedingt gefunden werden muss oder nicht in akzeptabler Rechenzeit gefunden werden kann.

Geschichte

2000: Sonderausgabe einer wissenschaftlichen Zeitschrift über Ameisenalgorithmen[2]
2000: Gutjahr führt ersten Nachweis der Konvergenz für einen Ameisenalgorithmus[3]
2001: Erste Verwendung der Ameisenalgorithmen von Unternehmen (Eurobios und AntOptima)[4]
2001: Iredi u. a. veröffentlichen den ersten Multi-Ziel-Algorithmus[5]

Anwendungen

siehe auch Rucksackproblem

Busrouten, Müllabfuhr, Post- und Auslieferungsrouten.
Maschinenbelegungsproblem: Minimierung der Transportzeit bei räumlich weit auseinander liegenden Produktionsstätten: Realisiert bei Unilever in England und Vincent Darley von der Bios-Gruppe in Santa Fe (New Mexico).
Routenoptimierung zur Nachschubversorgung von Fertigungslinien mit minimalem Transportmitteleinsatz (Routenbildung, -führung, -taktung in Verbindung mit der Behälterauswahl); realisiert im layoutbasierten Logistikplanungssystem MALAGA mit Algorithmen von INPRO.
Beschickung von Lackieranlagen: Losbildung zur Minimierung der Farbwechsel: Realisiert bei DaimlerChrysler.
Fertigungssteuerung: Losbildung zur Minimierung der Rüstzeiten und der Einhaltung von Endterminen bei ebm-papst, St. Georgen; realisiert durch ein Programm von Carpe Retem.
Proteinfaltung: 20 Aminosäuren werden zu Proteinen mit 100 Aminosäuren kombiniert → 20¹⁰⁰, dies ergibt etwa 10¹³⁰ verschiedene Proteine.
Telefonnetzwerk und Internet: Durch ACO können schnell freie Strecken gefunden werden und zwar während des Betriebs (z. B. Antnet).
Personaleinsatzplanung bei Fluggesellschaften: Flugbegleiter und Piloten werden unter Berücksichtigung von Ruhephasen etc. monatlich geplant.
Staplerleitsysteme: Optimale Steuerung und Auslastung von Fahrzeugen und Fahrwegen.

TSP mit ACO

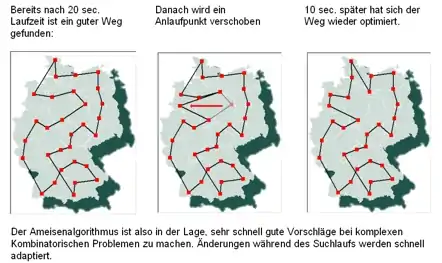
Bildschirmfotos eines Laufs für das Problem des Handlungsreisenden mit ACO

Das Problem des Handlungsreisenden (TSP) kann sehr effizient mit ACO bearbeitet werden. Im Beispiel wird TSP mit 30 „Städten“ bzw. Zielen berechnet (etwa 4,4·10³⁰ mögliche Wege). Die Stärke von ACO, Änderungen im laufenden Suchprozess selbstadaptiv zu verarbeiten, wird im Beispiel deutlich. Bei Verschieben eines Zielpunktes in der nach 20 Sekunden gefundenen Route wird bereits 10 Sekunden später (ohne Reinitialisierung) vom Algorithmus erneut ein guter Wegevorschlag gemacht (siehe Kombinatorik).

Literatur

M. Dorigo, M. Birattari, T. Stützle: Ant Colony Optimization: Artificial Ants as a Computational Intelligence Technique. In: IEEE Computational Intelligence Magazine. Volume 1, Nr. 4, 2006, S. 28–39.
Johann Dréo, Alain Petrowski, Éric Taillard, Patrick Siarry: Métaheuristiques pour l’optimisation difficile. Éd. Eyrolles, Paris 2003, ISBN 2-212-11368-4 (französisch, 356 S., extrait concernant les algorithmes de colonies de fourmis [PDF; 933 kB]).
Éric Bonabeau, Marco Dorigo, Guy Theraulaz: Swarm Intelligence: From Natural to Artificial Systems. Oxford University Press, 1999, ISBN 0-19-513159-2.
M. Dorigo, T. Stützle: Ant Colony Optimization. MIT Press / Bradford Books, Cambridge MA 2004, ISBN 0-262-04219-3.

Weblinks

ameisenalgorithmus.de (Memento vom 1. November 2010 im Internet Archive)
MIDACO-Solver Generelle Optimierungssoftware basierend auf dem Ameisenalgorithmus (Matlab, Excel, C/C++, R, Fortran, Python)
AntSim v1.1 Simulation des Ameisenalgorithmus (Windows)

Einzelnachweise

http://www.mathpages.com/home/kmath320/kmath320.htm
M. Dorigo, G. Di Caro et T. Stützle, special issue on "Ant Algorithms", Future Generation Computer Systems, volume 16, numéro 8, 2000.
W.J. Gutjahr, A graph-based Ant System and its convergence, Future Generation Computer Systems, volume 16, pages 873-888, 2000.
Eurobios und AntOptima.
S. Iredi, D. Merkle et M. Middendorf, Bi-Criterion Optimization with Multi Colony Ant Algorithms, Evolutionary Multi-Criterion Optimization, First International Conference (EMO’01), Zurich, Springer Verlag, pages 359-372, 2001.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] ttp://www.mathpages.com/home/kmath320/kmath320.htm

[2] M. Dorigo, G. Di Caro et T. Stützle, special issue on "Ant Algorithms", Future Generation Computer Systems, volume 16, numéro 8, 2000.

[3] W.J. Gutjahr, A graph-based Ant System and its convergence, Future Generation Computer Systems, volume 16, pages 873-888, 2000.

[4] Eurobios und AntOptima.

[5] S. Iredi, D. Merkle et M. Middendorf, Bi-Criterion Optimization with Multi Colony Ant Algorithms, Evolutionary Multi-Criterion Optimization, First International Conference (EMO’01), Zurich, Springer Verlag, pages 359-372, 2001.