Optische Täuschung
Eine optische Täuschung (von griech. optein = Sehen)[2] oder auch visuelle Illusion ist eine Täuschung der visuellen Wahrnehmung.
Optische Täuschungen können nahezu alle Aspekte des Sehens betreffen. Es gibt Tiefenillusionen, Farbillusionen, geometrische Illusionen, Bewegungsillusionen und einige mehr. In all diesen Fällen scheint das Sehsystem falsche Annahmen über die Natur des Sehreizes zu treffen, wie sich unter Zuhilfenahme weiterer Sinne oder durch Entfernen der auslösenden Faktoren zeigen lässt.
Optische Täuschungen werden in der Wahrnehmungspsychologie untersucht, da aus ihnen Rückschlüsse über die Verarbeitung von Sinnesreizen im Gehirn gewonnen werden können. Optische Täuschungen beruhen auf der Tatsache, dass Wahrnehmung auf unvollständiger Information beruht. Systematisch produziert und analysiert wurden optische Täuschungen zuerst in der Gestaltpsychologie.
Beispiele
Relativität von Linien
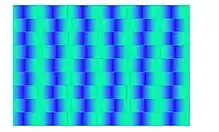
Das Quadrat im Bild links besteht aus schachbrettartig angeordneten dunklen und hellen Teilquadraten. In einigen der dunklen Teilquadrate sind die Ecken durch kleine helle Quadrate gestört. Es entsteht der Eindruck, als seien die – nachweislich geraden – Trennlinien zwischen den Teilquadraten wellenförmig gekrümmt. Dabei spielt deren Helligkeit und Dicke eine wesentliche Rolle.
Im Beispiel rechts oben scheinen die Querbalken keilförmig zu sein – in Wahrheit sind alle horizontalen Linien exakt parallel. Diese Täuschung wurde 1874 erstmals von Hugo Münsterberg (1863–1916), der sie auf einer amerikanischen Pferdebahnabokarte vorfand, beschrieben und im Jahre 1894/1897 als Die verschobene Schachbrettfigur veröffentlicht. Sie heißt deshalb auch Münsterberg-Täuschung. A. H. Pierce beschrieb sie 1898 im Titel einer Arbeit als Illusion of the Kindergarten Patterns, da sie an Flechtmuster im Kindergarten erinnert (in Psychological Review 5(3), 233–253). Der jüngste Name stammt von Richard L. Gregory, der sie 1973 nach einer schwarz-weiß gefliesten Wand in einem Café aus dem 19. Jahrhundert in der Innenstadt Bristols als Café Wall Illusion (Kaffeehaus-Täuschung) bezeichnete. Nach McCourt[3] kann die Café-Wall-Illusion über einen Helligkeitskontrast erklärt werden. Sind die Reihen schwarzer und weißer Felder durch schmale graue Linien getrennt, dann nimmt man diese zwischen schwarzen Feldern als deutlich heller wahr und zwischen hellen Feldern dunkler. Die Wahrnehmung verbindet nun die hell erscheinenden Linienabschnitte mit den Ecken der hellen Felder und entsprechend die dunkel erscheinenden Liniensegmente mit den Ecken der dunklen Felder. Diese subjektiven Konturen werden als zur Horizontalen geneigt wahrgenommen und lassen deshalb die Rechtecke keilförmig erscheinen. Der Effekt ist nicht auf ein Muster abwechselnd schwarzer und weißer Fliesen beschränkt, er tritt z. B. auch bei einer abgestuften oder kontinuierlichen Schattierung der Fliesen zwischen schwarz und weiß auf[4]. Die Illusion ist stark von der Breite und dem Grauwert der Trennlinie abhängig und erreicht ihr Maximum, wenn die Breite der Linie um einen Faktor zwei bis drei kleiner ist als das Auflösungsvermögen des Auges[5] (etwa eine Bogenminute, also 1/60 Sehwinkelgrad). Der Eindruck wellenförmig verlaufender Abgrenzungen kann auch entstehen, wenn Reihen mit ungleicher Periodenlänge kombiniert werden.[5] Es gibt auch farbige Versionen.[6]
Im vierten Beispiel (links unten) entsteht der Eindruck, die diagonalen Linien verliefen in einem spitzen Winkel zueinander, tatsächlich jedoch sind sie exakt gerade und parallel. Diese Illusion heißt auch Zöllner-Täuschung. Tauben empfinden diese Illusion im Vergleich zum Menschen genau umgekehrt, sie unterschätzen die Winkel zwischen den Linien.[7]
Einfluss der Flächentönung auf die Linientäuschung
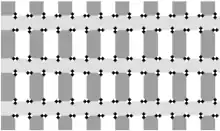
Die Grundlagen der nachfolgenden Illusion, deren Original von Victoria Skye stammt, gehen ursprünglich auf Akiyoshi Kitaoka zurück.[8] Die nicht-parallel erscheinenden hellgrauen Balken sind tatsächlich parallel. Außerdem wirken die dunkelgrauen Balken leicht geschwungen, obwohl sie in Wirklichkeit exakt parallel angeordnete Rechtecke darstellen (Abbildung rechts).
Ersetzt man jedoch den vorher hellen Grauton durch einen Farbton, der dunkler ist als der Farbton der vertikalen Balken, so verschwindet der ursprüngliche Täuschungseffekt. Die vorher nicht-parallel wirkenden Balken erscheinen nun wieder parallel, jedoch leicht gewellt (Abbildung links).
Relativität von Längen
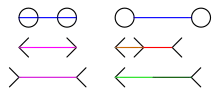
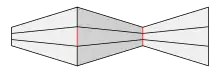
Das Beispiel im Bild links oben zeigt verschiedene Varianten der Müller-Lyer-Täuschung[9].
Die beiden blauen, die beiden pinkfarbenen, die braune und die rote sowie die hellgrüne und die dunkelgrüne Strecke sind jeweils gleich lang.
Der Betrachter nimmt jedoch unterschiedliche Längen wahr.
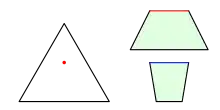
Im Bild rechts oben halbiert der rote Punkt im Innern des Dreiecks die senkrechte Dreieckshöhe. Für den Betrachter erscheint der Punkt jedoch weiter von der Dreiecksgrundseite entfernt als von der Spitze.[10]
Die rote und die blaue Strecke in den Trapezen sind gleich lang, obwohl die rote Strecke vom Betrachter als länger empfunden wird.
Im Bild links unten sind die beiden roten Strecken an den Mauerkanten gleich lang.
Die rechte Strecke empfindet der Betrachter jedoch als länger.
Auch hier handelt es sich um eine Variante der Müller-Lyer-Täuschung.[11]
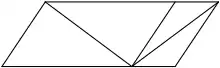
Im Bild rechts unten ist die nach dem Psychologen Friedrich Sander benannte Sandersche Täuschung[12] dargestellt: Die beiden eingezeichneten Parallelogrammdiagonalen sind gleich lang. Die Diagonale im größeren Parallelogramm erscheint jedoch merklich länger.
Relativität von Krümmungen
Im Bild links scheinen von links nach rechts die Krümmungsstärken der drei Kreisbögen abzunehmen.
Aus den im rechten Teil des Bildes dargestellten zugehörigen Vollkreisen wird jedoch ersichtlich, dass alle Radien identisch sind.
Somit haben auch alle Kreisbögen dieselben Krümmungen.[13]
Im Bild rechts erscheinen die beiden roten Parallelen, welche die sternförmig verlaufenden Geraden schneiden, gekrümmt. Tatsächlich sind sie jedoch parallel zueinander.
Diese Täuschung ist benannt nach dem deutschen Arzt und Physiologen Karl Ewald Konstantin Hering und wird als Hering-Täuschung[14] bezeichnet.
Relativität von Farben
Wenn man etwa eine halbe Minute lang das grüne Quadrat im Bild intensiv betrachtet und den Blick anschließend auf die freie Fläche daneben lenkt, so erscheint darauf als Nachbild ein Quadrat in der Komplementärfarbe rot.
Im Jahr 2015 wurde unter dem Stichwort #TheDress das Foto eines schwarz und blau gefärbten Kleids millionenfach auf Twitter verbreitet.[15] Auch zahlreiche Medien zeigten das Bild und meldeten, dass die meisten Menschen es auf dem überbelichteten Foto und aufgrund des gelblichen Lichts der Umgebung als weiß und gold-farbiges Kleid wahrnahmen. Die optische Wahrnehmung mancher Menschen korrigiert jedoch die Farbstichigkeit, so dass rund ein Fünftel der Betrachter das Kleid in den tatsächlichen Farben sahen. Eine Minderheit von Menschen sieht das Kleid manchmal in weiß-gold und manchmal in schwarz-blau.[16][17][18] In der Abbildung zeigt der Kasten auf der linken Seite, dass die optische Erscheinung des schwarz-blauen Kleids in gelbstichigem Licht identisch ist mit der Erscheinung des gelb-weißen Kleids in blaustichigem Licht, die im Kasten auf der rechten Seite dargestellt ist. Die beiden waagerechten Balken verbinden jeweils die identisch gefärbten Flächen, um dies zu beweisen.
Relativität von Helligkeit
Die Wahrnehmung von Helligkeitsunterschieden ist subjektiv. Ein Farbton, der in der Dämmerung als hell wahrgenommen wird, erscheint bei Sonnenlicht dunkel, und andersherum. Physikalisch ist diese Interpretation korrekt. Das Gehirn greift beim Betrachten der Beispiele auf der linken und rechten Seite auf diese Erfahrung zurück.
Im Bild links oben erscheint Grau im linken Bereich bei dunkler Umgebung heller, in heller Umgebung dunkler, obwohl der graue Balken überall den gleichen Grauwert besitzt (es sei denn, er wird im Winkel mittels eines Flachbildschirms betrachtet, bei dem generell eine tatsächliche Farbabweichung stattfindet). Außerdem scheint die Kontur an allen Stellen deutlich erkennbar zu sein, obwohl das Bild in der Basisgröße einen mehrere Pixel breiten Bereich hat, in dem der Grauwert des Streifens mit dem des Hintergrundes identisch ist.
Das Quadrat B rechts im Bild liegt im Schatten. Gesehen wird es als ein weißes Quadrat, es erscheint viel heller als das dunkle Quadrat A. Absolut betrachtet haben beide Quadrate jedoch den gleichen Grauwert.
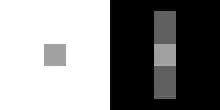
Die beiden kleinen grauen Quadrate im Bild links unten haben exakt den gleichen Grauwert, obwohl das rechte Quadrat deutlich heller erscheint als das linke Quadrat.
Dies zeigt besonders eindrucksvoll, wie sehr die Wahrnehmung des Betrachters von der Farbgebung umliegender Flächen abhängt.[19]
Munker-White-Illusion
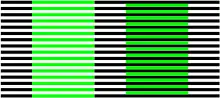
Bei der Munker-White-Täuschung werden zwei senkrechte grüne Balken jeweils von waagerechten weißen bzw. schwarzen Streifen durchkreuzt. Die beiden grünen Balken haben exakt denselben Farbton, obwohl sie in verschiedenen Grüntönen wahrgenommen werden. Der rechte grüne Balken erscheint deutlich dunkler als der linke.
Der Helligkeitseffekt wurde von Michael White beschrieben. Munker untersuchte zusätzlich Farbverschiebungen.[20]
Die Durchkreuzung des rechten grünen Balkens durch die schwarzen Streifen bewirkt die scheinbare Verdunklung des grünen Farbtons. Dies wird deutlich, wenn ein Teil der schwarzen Streifen, die den rechten grünen Balken kreuzen, entfernt wird.
Bezold-Effekt
Der Bezold-Effekt ist eine visuelle Wahrnehmungstäuschung. Benannt wurde er nach seinem Entdecker, dem deutschen Physiker und Meteorologen Johann Friedrich Wilhelm von Bezold.
Im linken Bild werden die blauen Balken in Kombination mit den weißen Zwischenräumen in der linken Hälfte heller wahrgenommen als mit den schwarzen Zwischenräumen in der rechten Hälfte.
Im rechten Bild erscheinen die grünen Kreisringe in der weißen Umgebung der linken Hälfte heller als in der braunen Umgebung der rechten Hälfte.
Chevreul-Täuschung
Die Chevreul-Täuschung (englisch: Chevreul's illusion) ist nach dem französischen Chemiker Michael Eugène Chevreul (1786–1889) benannt. Die Abbildung zeigt homogene graue Streifen abnehmender Helligkeit mit dem Effekt, dass an den Kanten eine Kontrastverstärkung durch die Aufhellung der helleren gegenüber der Verdunklung der dunkleren Flächen wahrgenommen wird. Das wahrgenommene Helligkeitsprofil erscheint nicht treppenstufenförmig, sondern durch ein sägezahnförmiges Profil überlagert.
Die Chevreul-Täuschung kann als Spezialfall der Mach’schen Bänder aufgefasst werden.[21]
Weitere Helligkeitstäuschungen
Das linke Bild zeigt die Bressansche Täuschung. Obwohl alle grauen Quadrate exakt denselben Farbton haben, erscheinen sie links heller als rechts.[22]
Die White-Täuschung ist im rechten Bild dargestellt. Obwohl alle grauen Balken exakt denselben Farbton haben, erscheinen sie links heller als rechts.[23]
Das Hermann-Gitter
Das Hermann-Gitter wurde von Ludimar Hermann im Jahre 1870 vorgestellt. Da dieses Phänomen auch von Ewald Hering bemerkt wurde, bezeichnet man es auch als Hering-Gitter. In den Schnittpunkten der weißen Linien (den „Kreuzungen“) sieht man schattenartige Flecken, jedoch nur dort, wohin man nicht fixiert.
Bisher wurde angenommen, dass der Effekt auf lateraler Hemmung beruht,[24] und in gängigen Lehrbüchern wird dies auch so dargestellt. Inzwischen gilt diese Theorie jedoch als widerlegt.[25][26][27][28][29][30] Ändert man nämlich die Täuschung nur leicht ab, z. B. durch sinusförmige Balken, so verschwindet die Illusion.[26] Diese Eigenschaft widerspricht der Theorie der lateralen Hemmung.
Das Szintillations-Gitter
Das Szintillations-Gitter (scintillating grid illusion) ist eine Illusion, die von E. und B. Lingelbach sowie M. Schrauf 1994 entdeckt wurde.[31] Sie wird oft als Variante des Hermann-Gitters betrachtet, besitzt aber andere Eigenschaften.[31][32] Wie das Hermann-Gitter besteht es aus schwarzen Quadraten die von helleren „Straßen“ getrennt sind, aber im Unterschied zum Hermann-Gitter sind die Straßen nicht weiß, sondern grau und auf den „Kreuzungen“ sind weiße Kreisscheibchen überlagert. Der optische Effekt führt dazu, dass man immer wieder schwarze Kreise an den Kreuzungen aufblinken sieht, die nicht im Blickfokus stehen. Zum Auftreten der Illusion darf das Bild nicht zu weit entfernt oder zu nah sein.
Relativität von Größe
Das Bild links ist ein Beispiel für viele ähnliche Schemazeichnungen, die die menschliche Wahrnehmung verwirren. Die linke orange Kugel ist kleiner als die umgebenden blauen, bei der rechten ist es umgekehrt. Die Übertragung von relativ kleiner und relativ größer auf die beiden orangen Kugeln in direkten Vergleich ist falsch. Beide orangen Kugeln sind gleich groß.
Das Bild rechts zeigt einen Säulengang und drei Schwesternpaare. Das Paar im Vordergrund erscheint kleiner als das mittlere Paar. Das hintere Paar erscheint am größten. Nachmessen beweist, dass alle drei Paare gleich groß sind. Das Auge liefert das Bild auf der Netzhaut, seine Bedeutung erschließt sich jedoch erst durch die Verarbeitung der Bildinformationen im Gehirn. Obwohl das Bild zweidimensional ist, wird ein Weg erkannt, der von vorn nach hinten verläuft und den Eindruck räumlicher Tiefe vermittelt. Daraus wird geschlossen, dass sich Gegenstände am unteren Rand in der Nähe befinden und Gegenstände in der Bildmitte weiter entfernt sind.
Die Bildverarbeitung im Gehirn geht davon aus, dass Gegenstände mit zunehmender Entfernung kleiner werden. So verwundert es nicht, dass die Frau hinten rechts im roten Mantel verglichen mit den Personen links im Bild extrem klein ist, obwohl sie nur weiter entfernt als die Personen im Vordergrund steht.
Das Paar im Vordergrund wirkt sehr klein, denn die Entfernung wird als gering interpretiert. Wäre es in Wirklichkeit genauso groß wie das mittlere Paar, müsste es auf dem Bild größer erscheinen. Da es auf dem Bild aber exakt genauso groß wie das mittlere Paar ist, folgert das Gehirn, dass die Personen in Wirklichkeit kleiner sein müssen. Das Gleiche gilt für das hintere Paar. Eigentlich müsste seine Größe der der Frau im roten Mantel entsprechen. Stattdessen wird es in mehr als doppelter Größe gesehen. Der Bildverarbeitungsprozess erfasst diese beiden Personen im Hintergrund als Riesen.
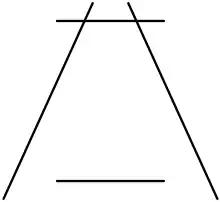
Die Relativität von Größe ist in der Ponzo-Täuschung bedeutungsvoll. Diese Illusion ist auch unter dem Namen Railway Lines Illusion bekannt, da die Figur an Eisenbahnschienen erinnert. Sie wurde vom italienischen Psychologen Mario Ponzo 1913 entwickelt. Zwei Balken werden gleich groß auf zwei (oder mehr Linien, die wie gerade Zuggleise verlaufen) gemalt. Der obere Balken wirkt größer. Haupterklärung ist das Prinzip der Größenkonstanz. Die zusammenlaufenden Schienenlinien werden als eigentlich parallele Linien aufgefasst, die in großer Tiefe ihren Fluchtpunkt haben. So entsteht der Eindruck räumlicher Tiefe. Der obere Balken wird aufgrund der räumlichen Interpretation dadurch als weiter entfernt wahrgenommen und müsste deshalb eigentlich wesentlich kleiner sein als der untere Balken, um als gleich groß wahrgenommen zu werden. Da aber die Netzhautbilder beider Balken gleich groß sind, wirkt der obere Balken größer.
Diese optische Täuschung macht man sich in Architektur, Fotografie und Film unter dem Begriff erzwungene Perspektive zunutze, um Objekte im Auge des Betrachters größer oder entfernter erscheinen zu lassen.
Relativität des Blickwinkels
Eine andere Art der optischen Täuschung entsteht durch den Blickwinkel des Betrachters. Man kann zum Beispiel Objekte bauen, die nur aus einem ganz bestimmten Blickwinkel gesehen wie ein gewöhnlicher Gegenstand, etwa ein Stuhl oder ein Klavier, aussehen, obwohl sie in Wahrheit eine völlig andere, verzerrte, räumliche Form haben. Oder man kann Objekte bauen, die aus einem ganz bestimmten Blickwinkel gesehen räumliche Figuren simulieren, die in der Realität gar nicht möglich sind, etwa das nebenstehende Penrose-Dreieck.
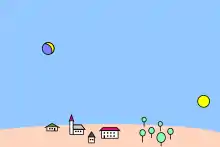
Unter das Stichwort „Relativität des Blickwinkels“ kann auch die „falsche“ Mondneigung eingeordnet werden. Dieses Phänomen kann beobachtet werden, wenn Mond und Sonne tagsüber gleichzeitig am Himmel zu sehen sind. Man würde erwarten, dass der Mond seine beleuchtete Seite, die Sichel, der Sonne zuwendet, weil sie von dort ihr Licht erhält. Stattdessen weicht die Sichel mit ihrer Symmetrieachse deutlich und manchmal sogar stark nach oben von der erwarteten Richtung ab. Die Sichel schaut über die Sonne hinweg, wie das nebenstehende Bild zeigt. Ebenso unerwartet zeigt die Sichel nachts trotz untergegangener Sonne manchmal nach oben statt nach unten. Diese Erscheinung ist eine optische Täuschung, für die es unterschiedliche Erklärungen gibt, unter anderem die, dass die Täuschung von der Blickrichtung abhängt.[33][34][35][36]
Unterschiedliche Wahrnehmung identischer Bilder
Die Abbildung auf der rechten Seite zeigt nebeneinander zwei Fotos einer Allee. Der Betrachter gewinnt den Eindruck, dass die Allee im rechten Foto etwas flacher ansteigt als die im linken Foto und dass die Allee im rechten Foto die im linken Foto kreuzt. In Wirklichkeit aber wurden die beiden Bilder nicht unter verschiedenen Winkeln aufgenommen, sondern sind exakt identisch.
Zwar gibt es bisher noch keine schlüssigen Erklärungen für dieses Phänomen, jedoch erscheint es am plausibelsten, dass unser Gehirn die Schnittstelle der zwei Straßen in der unteren Bildhälfte als eine Art Gabelung interpretiert und daraus folgert, dass die beiden Straßen nicht gleich verlaufen können, da sie sich ja sonst nicht kreuzen würden.[37]
Auf der linken Seite sind nebeneinander zwei Fotos abgebildet, die einen Teil der Westfassade des Altenberger Doms zeigen. Auch hier sind beide Bilder genau identisch, obwohl der Fassadenteil im linken Teil des Bildes schiefer erscheint als der im rechten Teil.
Dieser Effekt gewann den ersten Preis beim Illusion-of-the-year contest im Jahr 2007.[38]
Nicht vorhandene Objekte
Durchbrochene Linien der Ehrenstein-Täuschung
Flecke, Linien, Würfel?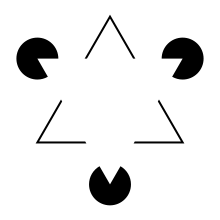
Kanizsa-Dreieck
Scheinkonturen einer Kugel
Bei manchen Sinneseindrücken glaubt der Betrachter Objekte wahrzunehmen, die nicht vorhanden sind. Ein Beispiel dafür ist das abgebildete Muster (links) aus durchbrochenen Linien. Der Betrachter glaubt, an den Schnittstellen weiße Scheiben zu sehen.
Im Beispiel in der Mitte sieht der Betrachter einen Würfel (den Necker-Würfel). Die Kanten, die auf dem Bild gar nicht vorhanden sind, werden in der Wahrnehmung ergänzt. Beim Kanizsa-Dreieck (benannt nach Gaetano Kanizsa) im Bild ganz rechts glaubt der Betrachter, ein weißes Dreieck zu sehen, obwohl im Bild nur Linien und Kreissegmente vorhanden sind. Die gedachten Linien (illusory contours) sind in der Literatur auch als „kognitive Konturen“ (cognitive contours[39]) bekannt geworden.
Ähnlich lassen sich auch die Marskanäle oder das Marsgesicht auf das Bestreben des Wahrnehmungssystems zurückführen, bei der Mustererkennung Bekanntes wiederzuentdecken.
Mehrdeutige Objekte / Kippfiguren
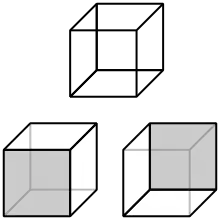
Kippfiguren wie der Necker-Würfel sind ein Beispiel für multistabile Wahrnehmung. Dabei bestimmt die Erfahrung die Lage, in der die Figur vorzugsweise wahrgenommen wird. Bei längerem Betrachten des Bildes kippt der Necker-Würfel.
Weitere Beispiele zur bistabilen Wahrnehmung sind die Rubinsche Vase, das Boring-Bild „Junge-Frau-Alte-Frau“ und die Hase-Ente-Illusion.
Bewegungsillusionen
Es gibt eine lange Reihe optischer Täuschungen, in denen der Betrachter meint, dass sich Teile des Bildes bewegen. Dabei muss manchmal der Kopf selbst bewegt werden und manchmal nicht. Letztere Variante funktioniert am besten mit peripherem Sehen, das heißt, die Bewegung ist an den Stellen zu erkennen, die gerade nicht fokussiert werden.
Eine Bewegungsillusion tritt auch auf, wenn man ein kleines Objekt vor einer Umgebung betrachtet, die keine Anhaltspunkte für die räumliche Lage gibt. Ein einsamer Stern am dunklen Himmel scheint sich zu bewegen.
Auch können statische Bilder eine Bewegungsillusion hervorrufen, ohne dass man seinen Kopf bewegt. Die Ursache findet sich in wiederholten Mustern, innerhalb derer sich unterschiedlich starke Kontraste befinden. Durch die unterschiedlich schnelle Weiterleitung von unterschiedlich starken Kontrasten und Helligkeiten in der Peripherie der Retina kommt es in den nachgeschalteten Ebenen der visuellen Verarbeitung (Stichwort: Reichardt-Detektoren) zur Falschverarbeitung und somit zur Fehlinterpretation. Die „Rotating Snake“ ist ein sehr gutes Beispiel dafür.
Weitere Beispiele
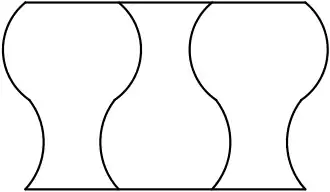
Ein Ames-Raum, benannt nach Adelbert Ames, Jr. (1880–1955), ist ein Raum mit einer speziellen Geometrie, in dem sich eine Reihe von optischen Täuschungen realisieren lassen.
Eine Reihe weitere optischer Täuschungen sind teils seit der Antike bekannt, teils erst im 19. Jahrhundert und in jüngster Vergangenheit beschrieben. Dazu gehören:
- Anamorphose
- Barber-Pole-Illusion
- Bourdon-Täuschung (Benjamin Bourdon, 1902)
- Delboeuf-Täuschung
- Fehlendes-Quadrat-Rätsel
- Fraser-Spirale
- Hollow-Face-Illusion
- Hybridbild
- Machsche Streifen (Ernst Mach, 1865)
- Mondtäuschung
- Mueller-Lyer-Illusion (Franz Müller-Lyer, 1889)
- Neon-Effekt
- Oppel-Täuschung (Johann Joseph Oppel,1855)
- Poggendorff-Täuschung (Johann Christian Poggendorff, 1860)
- Pulfrich-Effekt (Carl Pulfrich, 1922)
- Stürzende Linien und Sonnenstrahlen
- T-Figur-Illusion
- Unmögliche Figur
- Vexierbild
- Wasserfarbeneffekt (Baingio Pinna, John S. Werner und Lothar Spillmann, 2003)
Optische Täuschungen im Alltag
Dass optische Täuschungen auch im Alltag auftreten können, zeigen diese Beispiele:
- Bei einem Film erzeugt das schnelle Hintereinander von statischen Einzelbildern die Illusion einer Bewegung. Dabei handelt es sich um die sogenannte Beta-Bewegung, die unter gewissen Voraussetzungen nicht von einer echten Bewegung unterschieden werden kann. Wenn aber beim Fernsehen oder im Kino die Wiederholfrequenz der Bilder in einem gewissen Verhältnis zur Frequenz eines dargestellten, periodisch bewegten Objekts steht, kann es zu unwirklichen Bewegungserschienungen kommen, wie stillstehende oder rückwärts rotierende Wagenräder. Dies wird als stroboskopischer Effekt bezeichnet.
- Unter bestimmten landschaftlichen Gegebenheiten scheinen Straßen, die in Wirklichkeit bergabwärts verlaufen, bergaufwärts zu führen und umgekehrt (beispielsweise der Electric Brae in Schottland).
- In der illusionistischen Malerei werden mittels Trompe-l’œil-Technik Räume optisch vergrößert.
- Auch die Op-Art setzt optische Täuschungen gezielt als Stilmittel ein.
Die rote Linie scheint gekrümmt, tatsächlich ist sie gerade.
Die Umrandung der Grafik ist ein Rechteck, scheint sich aber nach rechts zu verjüngen.
Das Bild des Hahnentrittmusters scheint nach rechts gekippt.
Bei dieser textilen Wandbekleidung scheinen die tatsächlich parallelen Linien sich zu verjüngen.
Der Text erscheint unscharf, tatsächlich sind aber nur zusätzliche parallele, scharfe Linien eingezeichnet.
Mögliche Erklärungen für optische Täuschungen
Ein möglicher Lösungsansatz für „optische Täuschungen“ ist die Theorie des Amerikaners Mark Changizi. Dieser spricht von einem „Blick in die Zukunft“, die das Gehirn jede Sekunde vornimmt. Die visuellen Informationen der Außenwelt gelangen über die Netzhaut und die Sehnervenkreuzung ins Gehirn. Jedoch ist nur in einem kleinen Teil der Netzhaut scharfes Sehen möglich. Beim Betrachten einer visuellen Szene führt das Auge gezielte Bewegungen aus (Willkürsakkaden). Die unscharfen Bilder während der Augenbewegung werden vom Gehirn unbewusst ausgeblendet. Aus den verschiedenen Seheindrücken gelangen die Impulse über einen Teil des Thalamus (Corpus Geniculatum Laterale) und danach in das primäre Sehzentrum am Hinterhauptspol, dem primären Sehzentrum. Es gibt jedoch bereits auf dieser Ebene Rückkopplungschleifen, so dass bereits im Sehzentrum nur noch ca. 10 % der Nervenfasern vom Auge kommen. Bereits auf dieser Ebene findet eine essentielle Vorverarbeitung der Signale aufgrund biologischer Parameter und Vorerfahrungen statt. Im Wesentlichen erschafft das Gehirn also die visuelle Repräsentation des Gesehenen aus relativ schwachen Signalen selbst.[40] Dieser Mechanismus ist störanfällig, was die optischen Täuschungen verdeutlichen. Das Hirn wertet die Informationen dann weiter aus und errechnet die erwartete Veränderung für die Zukunft, dies ist evolutionär gesehen wichtig. Beispielsweise suggerieren Fluchtpunkte eine Bewegung, das Gehirn berechnet die Umgebung daraus neu. Da sich die reale Position jedoch nicht verändert, entsteht die optische Täuschung, dass Linien verbogen werden. Laut Changizi lassen sich so bis zu 50 Täuschungen erklären.[41]
Philatelistisches
Mit dem Erstausgabetag 10. Oktober 2019 gab die Deutsche Post AG in der Serie Optische Täuschungen zwei Postwertzeichen im Nennwert von 60 (Motiv: Gebogene Linien) und 80 Eurocent (Motiv: Perspektivwechsel) heraus. Die Entwürfe stammen vom Grafiker Thomas Steinacker aus Bonn. Mit dem Erstausgabetag 2. September 2021 folgte ein weiteres Postwertzeichen der Serie im Nennwert von 190 Eurocent mit dem Motiv Scheinbare Bewegung. Der Entwurf stammt vom Grafiker Thomas Steinacker aus Bonn.
Literatur
- artcolor: Optische Täuschungen – Illusions d'optique, Eggenkamp VerlagsgesellschaftmbH, Ascheberg 2003, ISBN 3-89743-373-7.
- Brad Honeycutt: Optische Illusionen, ars edition, 2013, 160 S., ISBN 978-3-8458-0042-4
- Ernst Mach: Über die Wirkung der räumlichen Verteilung des Lichtreizes auf die Netzhaut. In: Sitzungsberichte der mathematisch-naturwissenschaftlichen Classe der kaiserlichen Akademie der Wissenschaften Nr. 52, 1865, S. 303–322.
- Ludimar Hermann: Eine Erscheinung simultanen Contrastes. In: Pflügers Archiv für die gesamte Physiologie Nr. 3, 1870, S. 13–15.
- William H. Ittelson: The Ames Demonstrations in Perception. Princeton University Press, Princeton 1952.
- Franz C. Müller-Lyer: Optische Urtheilstäuschungen. In: Archiv für Physiologie Supplement-Band. 1889, S. 263–270.
- Hugo Münsterberg: Die verschobene Schachbrettfigur. In: Zeitschrift für Psychologie Nr. 15, 1897, S. 184–188.
- Jürg Nänni: Visuelle Wahrnehmung / Visual Perception. Niggli Verlag, Sulgen/Zürich 2008, ISBN 978-3-7212-0618-0.
- Nigel Rodgers: Unglaubliche optische Illusionen. Bechtermünz-Verlag, 1999, 228 Seiten, ISBN 978-3-8289-2318-8.
- Romana Karla Schuler: Seeing Motion. A History of Visual Perception in Art and Science. De Gruyter, Berlin/Boston 2016, ISBN 978-3-11-042696-0
- Uwe Stoklossa: Blicktricks. Anleitung zur Visuellen Verführung. Hermann Schmidt, Mainz 2005, ISBN 978-3-87439-681-3.
- Barton L. Anderson: A theory of illusory lightness and transparency in monocular and binocular images: the role of contour junctions. Perception 26:419–453 (1997)
- Raiten Taya, Walter H. Ehrenstein, C. Richard Cavonius: Varying the strength of the Munker-White effect by stereoscopic viewing. Perception 24:685–694 (1995)
- Michael White: A new effect on perceived lightness. Perception 8:413–416 (1979)
- Michael White: The effect of the nature of the surround on the perceived lightness of gray bars within square-wave test gratings. Perception 10:215–230 (1981)
- David Corney, R. Beau Lotto: What Are Lightness Illusions and Why Do We See Them? PLoS Comput Biol 3:e180 (2007)
Weblinks
- Sammlungen mit Hintergrundinformationen
- 48 optische Täuschungen zusammengestellt und kommentiert von Michael Bach
- Ausführlicher Fachartikel über optische Täuschungen
- A. Strahl: Täuschung des Gesichtssinns. Vortrag (PDF-Datei; 2,1 MB) oder als Flash-Animation. strahl.info
- 12 faszinierende optische Täuschungen, die das Auge betrügen (in englischer Sprache; Original-Titel: 12 fascinating optical illusions show how color can trick the eye). In: The Washington Post. 27. Februar 2015. Abgerufen am 27. Februar 2020.
- Arbeiten über einzelne Phänomene
Einzelnachweise
- Der Effekt, dass man zudem nicht zuordnen kann, ob der Mann auf dem Foto auch der Fotograf ist (trifft zu), kommt von einer Art verschachtelter optischer Täuschung: Das Originalfoto (Quellbild) ist etwas größer und zeigt noch einen Teil der Vorderseite des Kamera-Smartphones (das der Mann in der Hand hält) als Spiegelung. Dieser Teil wurde im obigen Bild weggeschnitten.
- In der wissenschaftlichen Literatur und auf wissenschaftlichen Kongressen zu dem Thema wird oft dem Begriff „visuelle Illusion“ (engl. visual illusion) der Vorzug gegeben, um dem Missverständnis vorzubeugen, dass die Täuschung etwas mit der Optik des Auges zu tun hat (dies ist nur für sogenannte „physikalische [visuelle] Täuschungen“ der Fall). Das Adjektiv optisch leitet sich vom griechischen Begriff optein = Sehen ab, nicht von Optik als einem Teilgebiet der modernen Physik. Regelmäßige wissenschaftliche Quellen zu visuellen Illusionen sind die englischsprachige Zeitschrift Perception und die Online-Schwesterzeitschrift i-Perception.
- M. E. McCourt: Brightness induction and the Café Wall illusion. „Perception“ Nr. 12, 1983. S. 131–142.
- A. Kitaoka, B. Pinna, G. Breistaff: Contrast polarities determine the direction of Café Wall tilts. „Perception“ Nr. 33, 2004. S. 11–20.
- Subjective contours triggered by border lines below the resolution limit. bei uni-ulm.de
- R. L. Gregory: Vision with isoluminant color contrast: 1. A projection technique and observations. Perception Nr. 6, 1977. S. 113–119.
- S. Watanabe, N. Nakamura, K. Fujita (2011). Pigeons perceive a reversed Zöllner illusion. „Cognition“ Nr. 119 (1). S. 137–141.
- Skyes schräges Gitter aus michaelbach.de, abgerufen am 18. Mai 2021
- Inga Menkhoff: Die Welt der optischen Illusionen, Parragon Books Ltd., S. 14 und 15.
- Inga Menkhoff: Die Welt der optischen Illusionen, Parragon Books Ltd., S. 19.
- Inga Menkhoff: Die Welt der optischen Illusionen, Parragon Books Ltd., S. 15.
- Sandersche Täuschung Dorsch – Lexikon der Psychologie, abgerufen am 30. Dezember 2021
- Inga Menkhoff: Die Welt der optischen Illusionen, Parragon Books Ltd., S. 27.
- Lexikon der Neurowissenschaft (spectrum.de über die Hering-Täuschung)
- siehe den entsprechenden Artikel der englischen Wikipedia: The dress
- The Science of Why No One Agrees on the Color of This Dress. In: Wired Magazine, Wired Magazine. Abgerufen am 28. Februar 2020.
- The inside story of the 'white dress, blue dress' drama that divided a planet. In: The Washington Post. Abgerufen am 27. Februar 2020.
- Why that dress looks white and gold: It's overexposed. In: Mashable. Abgerufen am 27. Februar 2020.
- Inga Menkhoff: Die Welt der optischen Illusionen, Parragon Books Ltd., S. 50.
- Munker-White-Täuschung aus michaelbach.de, abgerufen am 15. Mai 2021
- Chevreul-Täuschung Dorsch – Lexikon der Psychologie, abgerufen am 18. Mai 2021
- Bressan'sche Täuschung Dorsch – Lexikon der Psychologie, abgerufen am 18. Mai 2021
- White-Täuschung Dorsch – Lexikon der Psychologie, abgerufen am 18. Mai 2021
- G. Baumgartner: Indirekte Größenbestimmung der rezeptiven Felder der Retina beim Menschen mittels der Hermannschen Gittertäuschung.. In: Pflügers Arch ges Physiol. 272, 1960, S. 21–22. doi:10.1007/BF00680926.
- B. Lingelbach, B. Block, B. Hatzky, E. Reisinger: The Hermann grid illusion–retinal or cortical?. In: Perception. 14, Nr. 1, 1985, S. A7.
- J. Geier, L. Bernáth: Stopping the Hermann grid illusion by simple sine distortion. In: Perception. 33, 2004, S. 53.
- Peter H. Schiller, Christina E. Carvey: The Hermann grid illusion revisited Archiviert vom Original am 12. Dezember 2011. In: Perception. 34, Nr. 11, 2005, S. 1375–1397. doi:10.1068/p5447. Abgerufen am 1. Mai 2018.
- J. Geier, L. Bernáth, M. Hudák, L. Séra: Straightness as the main factor of the Hermann grid illusion. In: Perception. 37, Nr. 5, 2008, S. 651–665. doi:10.1068/p5622. PMID 18605141.
- János Geier: Stopping the Hermann grid illusion by sine distortion. 2008.
- Bach, Michael: Die Hermann-Gitter-Täuschung: Lehrbucherklärung widerlegt (The Hermann grid illusion: the classic textbook interpretation is obsolete). In: Ophthalmologe. 106, 2008, S. 913–917. doi:10.1007/s00347-008-1845-5.
- M. Schrauf, B. Lingelbach, E. Lingelbach, E. R. Wist: The Hermann Grid and the scintillation effect. In: Perception. 24 Suppl., 1995, S. 88–89.
- M. Schrauf, B. Lingelbach, E. R. Wist: The Scintillating Grid Illusion. In: Vision Research. 37, 1997, S. 1033–1038.
- Darstellung der „falschen“ Mondneigung mit Skizzen und geometrischen Berechnungen bei jimdo.com
- Astronomisch-psychologische Erklärung zur „falschen“ Mondneigung (PDF; 1,1 MB) bei psy-mayer.de
- Bernhard Schölkopf: The moon tilt illusion. (Memento vom 12. Dezember 2011 im Internet Archive) Zeitschrift Perception Nr. 27 (10), S. 1229–1232
- Georg Glaeser, Karlheinz Schott: Geometric Considerations About Seemingly Wrong Tilt of Crescent Moon. „KoG“ Nr. 13, S. 19–26
- In Anlehnung an den Artikel in stern.de vom 7. Februar 2018: Optische Täuschung: Warum diese zwei Straßen das Netz verrückt machen.
- The Leaning Tower Illusion aus illusionoftheyear.com, abgerufen am 14. Mai 2021
- Richard L. Gregory: Cognitive contours. In: Nature. 238, 1972, S. 51–52.
- Chris Frith: Wie das Gehirn die Welt erschafft. Spektrum Wissenschaftlicher Verlag, Sachbuch 2010
- Heike Le Ker: Optische Täuschungen: Blick in die Zukunft trickst das Auge aus. Spiegel Online, 2008 (abgerufen am 11. Juni 2008)