Scheinkorrelation

Scheinkorrelation oder (engl.) spurious relationship bezeichnet eine Korrelation (Übereinstimmung oder Entsprechung) zwischen zwei Größen, der kein Kausalzusammenhang, sondern nur eine zufällige oder indirekte Beziehung zu Grunde liegt.

Die Anzahl der Störche und die menschliche Geburtenrate in einem Land: Beispiel für eine Scheinkorrelation

Der deutsche Begriff ist missverständlich, da eben eigentlich Scheinkausalität gemeint ist. Denn es liegt nicht nur scheinbar, sondern tatsächlich eine Korrelation vor (aber eben keine Kausalität; zur Abgrenzung der Konzepte siehe: Korrelation und Kausalzusammenhang). Ohnehin ist eine Korrelation ein statistischer Begriff, der weder Kausalität impliziert, noch von ihr impliziert wird.

Scheinkorrelation ist die statistische Entsprechung des in der Philosophie betrachteten Fehlschlusses Cum hoc ergo propter hoc (gemeinsames Auftreten impliziert keine Kausalität oder engl. correlation, not causation).

Eine Scheinkorrelation kommt z. B. vor, wenn konfundierende Variablen (Störvariablen) oder andere intervenierende Variablen einen Einfluss haben. Das Phänomen ist seit den Anfängen der Statistik bekannt; der Begriff spurious correlation wurde 1954 von Herbert A. Simon geprägt.

Beispiel

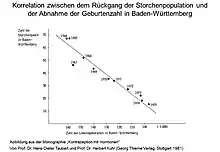
Ein bekanntes Beispiel ist die Korrelation zwischen der menschlichen Geburtenrate und der Zahl der Storchenpaare in verschiedenen europäischen Regionen.[1] Obwohl es eine Korrelation zwischen der Zahl der Geburten und der Zahl der Storchenpaare gibt (d. h. mehr Geburten, und gleichzeitig mehr Storchenpaare), gibt es keinen kausalen Zusammenhang (die falsche Schlussfolgerung, dass die Kinder vom Storch gebracht werden). Die Korrelation zwischen Geburten und Storchpaaren ergibt sich daraus, dass in ländlichen Regionen mehr Störche nisten und tendenziell auch mehr Kinder pro Paar geboren werden. Das Beispiel der Scheinkorrelation zwischen Störchen und der Geburt von Babys wurde von Jerzy Neyman (1952) vorgebracht.[2] Gegeben die Zahl der Frauen $X$ , Zahl der Geburten von Babys $Y$ , und die Zahl der Störche $Z$ , so können die Raten $r_{1}=Y/X$ und $r_{2}=Z/X$ berechnet werden. Zieht man nun unabhängig verteilte Stichproben der Zufallsvariablen und korreliert die Raten $r_{1}$ und $r_{2}$ erhält man aufgrund des gemeinsamen Nenners eine Scheinkorrelation.

Scheinregression

Die Scheinregression ist ein Spezialfall der Regression, bei der ein statistisch signifikanter Zusammenhang zwischen einer Variablen $Y_{t}$ und einer Variablen $X_{t}$ festgestellt werden kann, der sachlogisch nicht zu begründen ist. Scheinregressionen sind auf einen gemeinsamen Trend in den beteiligten Variablen zurückzuführen. Ein Hinweis auf Scheinregression ist ein hohes Bestimmtheitsmaß $R^{2}$ und ein Durbin-Watson-Koeffizient von nahezu Null (hohe positive Autokorrelation erster Ordnung). Darüber hinaus liefert der Dickey-Fuller-Test, insofern dieser eine Zeitreihe als nichtstationär identifiziert, ein Indiz für eine Scheinregression.

Regressionsgerade zwischen zwei unabhängigen AR(1)-Prozessen mit Einheitswurzel inklusive

t

-Statistik.

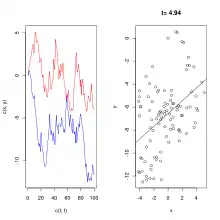
Ein Beispiel in den Anwendungen ist das spurious regression problem der Ökonometrie, auf welches Clive W. J. Granger und Paul Newbold 1974 hingewiesen haben, nach dem auch zwei unabhängige Random walks ohne deterministische Trendkomponente (oder andere Formen von stochastischen Prozessen mit Einheitswurzel) korrelieren, obwohl sogar stochastische Unabhängigkeit vorliegt.[3] Genauer formuliert führen solche durch Autokorrelation verursachte Verletzungen der Voraussetzungen eines Regressionsmodells dazu, dass zum Beispiel die Teststatistiken für die Hypothese, dass der Steigungsparameter der Regressionsgeraden gleich Null ist (t-Statistik), mit wachsendem Datenumfang divergieren, also wenn nur genügend Daten erhoben werden, immer ein Zusammenhang festgestellt wird.

Siehe auch

Literatur

Allgemeine Literatur

Günter Bamberg, Franz Baur, Michael Krapp: Statistik. 13. Auflage. Oldenbourg Wissenschaftsverlag, 2007, ISBN 978-3-486-58188-1.
Udo Kelle: Die Integration qualitativer und quantitativer Methoden in der empirischen Sozialforschung: theoretische Grundlagen und methodologische Konzepte. VS Verlag, 2007, ISBN 978-3-531-15312-4, S. 203.

Originalarbeiten

Herbert A. Simon: Spurious correlation: a causal interpretation. In: Journal of the American Statistical Association. Vol. 49, 1954, S. 467–479, doi:10.1080/01621459.1954.10483515 JSTOR 2281124.
Clive W. J. Granger, Paul Newbold: Spurious regressions in econometrics. In: Journal of Econometrics. Nr. 2, 1974, S. 111–120, doi:10.1016/0304-4076(74)90034-7.

Weblinks

Einzelnachweise

R. Matthews: Storks deliver babies (p= 0.008). In: Teaching Statistics. 22(2), 2000, S. 36–38, doi:10.1111/1467-9639.00013.
Gerald van Belle: Statistical Rules of Thumb, Second Edition (= Wiley Series in Probability and Statistics). John Wiley & Sons, Inc., Hoboken, NJ, USA 2008, ISBN 978-0-470-37796-3.
Christopher Dougherty: Introduction to Econometrics. 3. Auflage. Oxford University Press, 2007, ISBN 978-0-19-928096-4, S. 388. (Google-Books-Link)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] R. Matthews: Storks deliver babies (p= 0.008). In: Teaching Statistics. 22(2), 2000, S. 36–38, doi:10.1111/1467-9639.00013.

[2] Gerald van Belle: Statistical Rules of Thumb, Second Edition (= Wiley Series in Probability and Statistics). John Wiley & Sons, Inc., Hoboken, NJ, USA 2008, ISBN 978-0-470-37796-3.

[3] Christopher Dougherty: Introduction to Econometrics. 3. Auflage. Oxford University Press, 2007, ISBN 978-0-19-928096-4, S. 388. (Google-Books-Link)