Umgekehrte polnische Notation
Die umgekehrte polnische Notation (UPN) oder reverse polnische Notation[1] englisch reverse Polish notation (kurz RPN), auch Postfixnotation genannt, ist eine von der polnischen Notation abgeleitete Schreibweise bzw. Eingabelogik für die Anwendung von Operationen. Bei der umgekehrten polnischen Notation werden zunächst die Operanden niedergeschrieben bzw. eingegeben und danach der darauf anzuwendende Operator.

Größere Verbreitung fand die UPN nur durch die Taschenrechner des Herstellers Hewlett-Packard. Dessen Rechner besitzen eine meist auffällig große Enter-Taste, dafür fehlen die Klammertasten (, ) und die Gleichheitstaste =. Eine konventionelle Löschtaste zur Einleitung der Berechnung fehlt ebenfalls, da nicht mehr benötigte Ergebnisse während der Berechnungen automatisch aus dem Stapel geschoben werden. Eine modifizierte Löschtaste wird allerdings zur Beseitigung von Tippfehlern verwendet. Viele der größeren Taschenrechner von Hewlett-Packard, wie etwa die HP-48-Serie, unterstützen eine objektorientierte Abwandlung und Erweiterung von UPN/RPN namens RPL (für Reverse Polish LISP), die zwar auf den gleichen Grundprinzipien beruht, aber in einigen Details soweit abweicht, dass Eingabefolgen angepasst werden müssen.
Prinzip
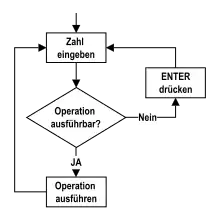
In der Informatik ist die UPN deshalb von Interesse, weil sie eine stapelbasierte Abarbeitung ermöglicht: Operanden werden beim Lesen auf den Stapel (Stack) gelegt, ein Operator holt sich die Anzahl an Operanden vom Stapel, die seiner Stelligkeit entspricht, und legt das Ergebnis der Operation wieder auf dem Stapel ab. Am Ende liegt dann das Ergebnis des Terms oben auf dem Stapel. Deshalb bildet die UPN die Grundlage für stapelbasierte Programmiersprachen wie Forth, RPL, PostScript oder die Anweisungsliste im SPS-Bereich. Eine andere Bezeichnung ist Nulladressmaschine, weil keine expliziten Speicheradressen im Spiel sind.
Beispiel: Es sollen 3 und 4 addiert werden. Die Operanden sind dann 3 und 4, der Operator ist „+“:
In der Schule ist die erlernte Notation die (sequenziell organisierende) Infixnotation „3+4“. In der umgekehrten polnischen Notation wird hingegen „3 4 +“ geschrieben (zwischen 3 und 4 ist ein Leerraum, damit die Zahlenfolge von der Zahl 34 unterschieden werden kann).
Weiteres Beispiel (in der Infixnotation): „(3+4)×5“. Bei der UPN können die Klammern entfallen, alle Operationen (hier „+“ und „ד) arbeiten mit den beiden oberen Elementen des Stapels. Das Beispiel heißt in UPN dann: „3 4 + 5 ד (zuerst wird der Klammerausdruck „3 4 +“ausgerechnet, danach die hierbei entstandene Zahl 7 mit 5 multipliziert).
Ein ähnliches Prinzip ist auch im Deutschen und anderen natürlichen Sprachen (SOV-Sprachen) zu finden, hierbei Scrambling genannt: In Infinitiven und Nebensätzen des Deutschen werden erst alle Ergänzungen (Argumente) eines Verbs hintereinander genannt, und am Schluss das Verb, das einem Operator gleicht, weil es die Ergänzungen zu einem Satz verknüpft:
- Die Wäsche mit Seife waschen.
- Das Mehl in einer Schüssel mit den Eiern verrühren
- wenn jemand dem Hund das Futter wegnimmt.
Sprachlich kann man die Unterschiede der Infixnotation „(3+4)×5“ und der UPN „3 4 + 5 ד daher wie folgt veranschaulichen:
- Statt „3 plus 4, und dann mal 5“ sagt man „3 und 4 addieren und mit 5 multiplizieren“.
Bei nicht-kommutativen Operationen ist die Reihenfolge in beiden Schreibweisen identisch.
Bei Operatoren mit nur einem Operanden ist UPN auch bei (Taschen-)Rechnern sehr gebräuchlich, die sonst mit der Infixnotation arbeiten. Beispiele dafür sind die trigonometrischen oder logarithmischen Funktionen, die bei den meisten Taschenrechnern in der Form 2 5 ln oder 2 5 sin eingegeben werden (der Operator „ln“ bzw. „sin“ wird nach dem Operanden „25“ eingegeben).
Für die Konversion zwischen den Schreibweisen lässt sich der Shunting-yard-Algorithmus verwenden.
Vorteile

Der auffälligste Vorteil der UPN ist, dass sie im Allgemeinen mit einer geringeren Anzahl von Tastendrücken auskommt. Um zum Beispiel die Rechnung (1+2)×(3+4) vorzunehmen, muss man im algebraischen Modus zwölf Tasten betätigen:
- ( 1 + 2 ) × ( 3 + 4 ) =
Bei vielen Implementierungen lässt sich die Tastenfolge noch optimieren; dies ist allerdings genaugenommen kein „algebraisches Vorgehen“:
- 1 + 2 = × ( 3 + 4 =
Im UPN-Modus sind nur neun Tastendrücke erforderlich:
- 1 Enter 2 + 3 Enter 4 + ×
Es sind also drei Tasten weniger zu drücken als im algebraischen Modus; bei aufwendigeren Rechnungen ist die Ersparnis entsprechend größer.
Ein weiterer Vorteil der UPN ist es, dass die Rechnung stets schrittweise und mit sichtbaren Zwischenergebnissen ausgeführt wird; man kann die Daten also nach und nach weiterbearbeiten. Allerdings zeigen auch viele algebraische Taschenrechner Zwischenergebnisse, so weit es möglich ist, zum Beispiel beim Betätigen der )-Taste den Wert des aktuellen Klammerausdrucks.
Die Verfügbarkeit von Zwischenergebnissen erleichtert es nicht nur, die Eingaben zu kontrollieren und Fehler zu identifizieren, sondern erlaubt es im Zusammenhang mit den bei UPN verfügbaren Vertauschungsoperationen innerhalb des Stapels, jedes Zwischenergebnis einfach zu speichern, ohne dass dafür gesonderte Speicherregister benötigt würden, und später weiterzuverarbeiten. Insbesondere lässt sich der häufig vorkommende Fall, dass ein Operand gleich nochmals benötigt wird – wie etwa in der Rechnung (a−b)/b – ohne erneute Eingabe oder Speicherung von b rechnen; UPN-Rechner verfügen dafür über ein Register LASTX, das den letzten Operanden automatisch speichert.
Die Programmierung eines UPN-Rechners folgt normalerweise exakt der manuellen Eingabe einer Berechnung, was vor allem bei häufigen kurzen Rechenaufgaben sehr anwendungsfreundlich ist, weil keine gesonderte Programmiersprache erlernt werden muss. Bei algebraischen Taschenrechnern weicht das Programmiermodell oft (aber nicht immer) von der manuellen Formeleingabe ab.
Nachteile
Nachteil der UPN ist in erster Linie die Tatsache, dass sie häufig nicht aus dem täglichen Leben beziehungsweise der Schule vertraut ist und daher erst erlernt werden muss; hinzu kommt, dass die Vorteile erst beim intensiveren Gebrauch und vor allem bei der Arbeit mit komplizierten Formeln zu bemerken sind. Die Gewöhnung an eine der beiden Notationen kann den Umgang mit der jeweils anderen erschweren.
Umsetzung
In klassischen UPN-Rechnern werden vier Stack-Ebenen verwendet, die bei Hewlett-Packard mit X (Anzeigewert), Y, Z und T bezeichnet sind. Erste Umsetzungen mit nur zwei (Sinclair-Taschenrechner) oder drei Registern (X, Y und Z) hatten sich als unpraktisch erwiesen. Daneben gab es auch Implementierungen mit fünf Registern (Heathkit OC-1401). Seit neuerem existieren auch freie Implementierungen mit acht Stackebenen (X, Y, Z, T, A, B, C, D) (WP 31S und WP 34S). Aktuelle Implementierungen der HP-Taschenrechner ab der Baureihe HP 48 haben keine Begrenzung in der Anzahl der Stack-Ebenen (nur noch durch den Speicher begrenzt). Dadurch sind auch die Namenskonventionen insbesondere für die Register Z, T usw. entfallen. Aus Gründen der Tastaturbeschriftung sowie zum einfacheren Verständnis werden jedoch auch bei diesen Rechnern die ersten beiden Stack-Ebenen als Y und X bezeichnet (auch wenn sie programmatisch nicht mehr so adressiert werden). Der quasi vollkommene Wegfall der Stack-Ebenen-Limitierung hat einerseits den Vorteil, dass auch komplexere Rechnungen übersichtlich eingegeben sowie Zwischenergebnisse gespeichert werden können, aber auch den Nachteil, dass der Stack mit einer Tastenkombination gelöscht werden muss, um alte Ergebnisse zu entfernen.
Ein weiteres Register L (LASTX) speichert automatisch den letzten Wert von X. Zusätzlich ist eine Vertauschung von X und Y (wichtig für nicht-kommutative Operationen) sowie eine zyklische Vertauschung aller Stack-Register (roll down, der Wert von X gelangt nach T, der Wert von Y nach X usw.) implementiert. In besser ausgestatteten Rechnern ist auch die umgekehrte zyklische Vertauschung (roll up) und später (im HP-41) das beliebige Speichern und Zurückrufen von Stackregistern möglich.
Register T hat dabei eine Sonderfunktion. Operationen, die mehr als ein Argument haben, verschieben den Stack „nach unten“, und der Wert von T wird kopiert, was für fortgesetztes Rechnen sehr vorteilhaft sein kann. Frühe Umsetzungen löschten auf einigen Rechnern T (T clears on pop), was sich als weniger praktisch herausstellte. Es gab auch Modelle (wie den HP-35), die bei komplexen Operationen T als Zwischenspeicher benötigten und dessen Inhalt überschrieben. Bei Rechnern, die RPL unterstützen, ist die Tiefe des Stacks nur durch den zur Verfügung stehenden Speicherplatz beschränkt. Beim HP Prime ist sie auf 128 Stack-Ebenen begrenzt. Demzufolge entfällt dort auch die oben skizzierte Sonderfunktion des T-Registers.
Eine weitere Besonderheit betrifft die Funktion der ENTER-Taste, die bei Hewlett-Packard-Rechnern, die klassisches UPN (Classical RPN im englischen Sprachraum) implementieren, unter bestimmten Bedingungen den Inhalt des X-Registers automatisch in das Y-Register dupliziert, was bei UPN-Rechnern anderer Hersteller und auch bei RPL-Rechnern nicht geschieht. Auch alle neueren Hewlett-Packard-Rechner mit UPN-Unterstützung, die nicht eines der klassischen Modelle nachbilden, weichen in diesem Punkt von der klassischen UPN-Eingabelogik ab und arbeiten diesbezüglich stattdessen wie RPL. Diese Variante erfordert auch leichte Anpassungen in der Kommandoabfolge in Programmen und wird im englischen Sprachraum umgangssprachlich oft als Entry RPN (Eingabe-UPN) bezeichnet.
In der Vergangenheit, insbesondere in der Frühzeit elektronischer Taschenrechner, galt als wesentlicher Vorteil der UPN, dass sie sich mit geringerem Hardwareaufwand realisieren lässt. Die Praxis zeigt, dass sich relativ komplexe mathematische Berechnungen mit einem Stapel von nur vier Einträgen ausführen lassen. Demgegenüber muss ein algebraischer Taschenrechner für jede Klammerebene und allgemein für jedes Zwischenergebnis („Punkt- vor Strichrechnung“), das er verarbeiten soll, ein eigenes Register besitzen; in der Praxis wurden algebraische Taschenrechner mit bis zu zwölf Operandenregistern zur Speicherung von bis zu elf unvollständigen Operationen hergestellt. Mit der Leistungsfähigkeit der heutigen elektronischen Schaltkreise ist dieser theoretische Vorteil der UPN technisch nicht mehr bedeutsam, und es werden heute moderne UPN-Taschenrechner mit mehr als vier Stapelregistern und mit zusätzlichen Speicherregistern ausgestattet.
Algorithmen
Konvertierung von Infixnotation nach UPN
Ein arithmetischer Ausdruck in Infixnotation kann zeichenweise mit dem Shunting-yard-Algorithmus (deutsch: ‚Rangierbahnhof‘-Algorithmus) direkt in die UPN umgewandelt werden.
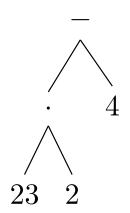
Bei der Darstellung eines Ausdrucks in Infixnotation als Term-Baum entspricht die UPN der Ausgabe der Knoten-Labels in einem Postorder-Traversal.
Beispiel:
Infixnotation:
Postorder-Traversal:
postorder(23*2-4)
-> postorder(23*2); postorder(4); print(-);
-> postorder(23); postorder(2); print(*); postorder(4); print(-);
-> print(23); print(2); print(*); print(4); print(-)
Postfix-Notation (UPN):
Definition: Analog zu einem Postorder-Traversal lässt sich die UPN formal über die Konvertierung von einem Infix-Ausdruck rekursiv definieren:
- Wenn der Infix-Ausdruck ein Operand ist, dann ist in UPN.
- Wenn der Infix-Ausdruck in der Form vorliegt, dann ist seine UPN durch definiert, wobei bzw. die UPN von bzw. bezeichnen.
- Wenn ein Infix-Ausdruck die Form hat, dann ist seine UPN, wobei die UPN von bezeichnet.
Anwendung
Die Umwandlung eines Infix-Terms nach UPN ist ein wichtiger Bestandteil beim Compilerbau.
Auswertung
Ein Ausdruck in UPN wird ausgewertet, indem er von links nach rechts gelesen wird, wobei Operanden auf einen Stack gelegt werden. Wird ein -stelliger Operator gelesen, werden Elemente vom Stack entfernt, der Operator auf diese angewendet und das Ergebnis auf den Stack zurückgelegt. Am Ende der Verarbeitung liegt das Gesamtergebnis der Berechnung auf dem Stack. Der folgende Pseudocode spezifiziert diesen Algorithmus:
compute_rpn(input)
stack_init
foreach (o in input)
switch o
isnumber
push o
isbinoperator
right = pop
left = pop
t = compute(left, o, right)
push t
return pop
Die Reihenfolge, in der die Operanden vom Stack entnommen werden, ist nicht beliebig. Sie ergibt sich direkt aus der Definition der Umwandlung von Infix-Ausdrücken in die UPN. Bei nicht-kommutativen Operatoren kann eine falsche Operandenfolge zu einem falschen Ergebnis führen.
Beispiel:
stack : [] o = 23 stack : [23] o = 2 stack : [23,2] o = * right = 2 stack : [23] left = 23 stack : [] t = 46 stack : [46] o = 4 stack : [46,4] o = - right = 4 stack : [46] left = 46 stack : [] t = 42 stack : [42]
Modelle
Es gibt im Vergleich zu rein algebraischen Taschenrechnern nur wenige Taschenrechnermodelle, die auch oder ausschließlich UPN unterstützen; der einzige etablierte Hersteller, der eine größere Zahl UPN-fähiger Geräte herstellt, ist Hewlett-Packard. Mit Ausnahme des seit 1981 erhältlichen reinen UPN-Taschenrechners HP-12C und einiger rein algebraischer Geräte im unteren Preisbereich unterstützen die Anfang 2007 neu auf den Markt gekommenen HP-Taschenrechner wie der HP-50g und der HP Prime beide Eingabenotationen.
Derzeit bietet auch das russische Unternehmen Semico aus Nowosibirsk Taschen- und Tischrechner mit UPN-Eingabe, allerdings ausschließlich mit kyrillischer Tastatur, an.[2] Seit 2012 stellt auch die schweizerische SwissMicros eine Reihe an unterschiedlichen UPN-Rechnern her, die sich überwiegend an Vorbildern von HP orientieren.
Der in Emacs integrierte Taschenrechner Calc verwendet optional die umgekehrte polnische Notation. Auf der Shell nahezu jedes Unix-Systems steht der Rechner dc zur Verfügung, der ebenfalls auf der umgekehrten polnischen Notation beruht. Auch der Rechner von macOS kann optional im UPN-Betrieb genutzt werden, wobei allerdings in früheren Versionen eine falsche Implementierung des Stacks die Benutzbarkeit einschränkte. Spätestens seit macOS 10.12 (Sierra) ist der Stack hier korrekt implementiert.
Darüber hinaus werden insbesondere im Open Source, Free- und Sharewarebereich etliche Programme angeboten, die UPN-Rechner emulieren bzw. die UPN verwenden.
Einige BASIC-Dialekte (insbesondere auf HP-Computern) haben zur internen Darstellung des Bytecodes die UPN-Form verwendet. Diese Rechner übersetzten die eingegebenen Programmzeilen (und arithmetischen Ausdrücke) in UPN und legten sie so im Speicher ab. Während der Laufzeit konnten die Ausdrücke damit mit maximaler Effizienz abgearbeitet werden, da keine arithmetischen Umformungen oder Prioritätenbetrachtungen mehr vorgenommen werden mussten. Insbesondere die HP-Computer der Serien 70 und 80 konnten auf diesem Wege trotz geringer Taktfrequenz hohe Verarbeitungsgeschwindigkeiten erzielen.
Geschichte
Die polnische Notation (auch Präfix-Notation oder Łukasiewicz-Notation) verdankt ihren Namen dem polnischen Mathematiker Jan Łukasiewicz, der sie in den 1920er-Jahren entwickelte (eine genauere Datierung ist wohl nicht möglich[3]). Łukasiewicz stellte die polnische Notation als kompakte und klammerfreie Schreibweise für die Aussagenlogik vor.
Łukasiewicz weist selbst darauf hin,[4] dass seine Schreibweise zwar die kompakteste und die erste linear geschriebene klammerfreie Schreibweise ist, aber nicht die erste klammerfreie Schreibweise überhaupt. Der Verdienst, die Logik von der Klammer befreit zu haben, kommt Gottlob Frege mit seiner bereits 1879 veröffentlichten Begriffsschriftnotation zu.
Der gleiche Effekt der Klammerfreiheit wird erreicht, wenn der Operator nicht vor den Operanden, sondern danach steht. Diese Variante der polnischen Notation, die als „umgekehrte polnische Notation“ bezeichnet wird, wurde vermutlich ebenfalls bereits von Łukasiewicz gesehen. Explizit angesprochen und praktisch verwendet wurde die umgekehrte polnische Notation allerdings wohl erst in den 1950er-Jahren vom australischen Philosophen Charles Hamblin.
Einzelnachweise
- Günter Jorke, Bernhard Lampe, Norbert Wengel: Arithmetische Algorithmen der Mikrorechentechnik. Auflage 1, VEB Verlag Technik, Berlin 1989 ISBN 3-341-00515-3 (books.google.de).
- mk.semico.ru
- „Die ältesten Texte in den ‚Selected Works‘, in denen Łukasiewicz polnische Notation verwendet, datieren relativ spät, sind aber Präsentationen vorangehender Arbeiten, die ‚in the course of the years 1920–1930‘ (S. 131) stattgefunden haben, also auch keine genauere Zeitangabe geben.“ (Ch. Gottschall: Logische Notationen und deren Verarbeitung auf elektronischen Rechenanlagen aus theoretischer, praktischer und historischer Sicht. (Diplomarbeit), Wien 2005, S. 88).
- On the history of the logic of propositions. In: Łukasiewicz: Selected Works. 1970.
Literatur
- Donald Knuth: The Art of Computer Programming, Volume 1: Fundamental Algorithms. 3. Auflage. Addison-Wesley, 1997, ISBN 0-201-89683-4, S. 338.
- Alfred V. Aho, Jeffrey D. Ullman: The Theory of Parsing, Translation, and Compiling, Vol. 1, Parsing. 1. Auflage. Prentice Hall, 1972, ISBN 0-13-914556-7, S. 214.
- Jan Łukasiewicz: Selected Works. Hrsg.: Ludwik Borkowski (= Studies in logic and the foundations of mathematics. Nr. 54). North-Holland Publishing Company/ Polish Scientific Publishers, Amsterdam/ Warschau 1970, ISBN 0-7204-2252-3.
- Charles L. Hamblin: Translation to and from Polish notation. In: The Computer Journal. Band 5, Nr. 3, 1962, S. 210–213, doi:10.1093/comjnl/5.3.210 (PDF).
Weblinks
- (Seite nicht mehr abrufbar, Suche in Webarchiven: Eine Einführung in die umgekehrte polnische Notation) bei HP
- Bob Brown: Postfix Notation Mini-Lecture. 6. Mai 2016 (englisch).
- Verwendung der RPN bei HP (englisch)
- Is it Really a Pathetic Name? Vortrag auf der HP Handheld Conference am, 22.–23. Sept. 2012 in Nashville (englisch)