Erfüllbarkeitsproblem der Aussagenlogik
Das Erfüllbarkeitsproblem der Aussagenlogik (SAT, von englisch satisfiability‚ Erfüllbarkeit‘) ist ein Entscheidungsproblem der theoretischen Informatik. Es beschäftigt sich mit der Frage, ob eine gegebene aussagenlogische Formel erfüllbar ist. Mit anderen Worten: Existiert eine Belegung der Variablen von mit den Werten wahr oder falsch, sodass zu wahr ausgewertet wird?
SAT gehört zur Komplexitätsklasse NP der Probleme, die von einer nichtdeterministischen Turingmaschine in polynomieller Zeit gelöst werden können. Außerdem war SAT das erste Problem, für das NP-Vollständigkeit nachgewiesen wurde (Satz von Cook). Damit kann jedes Problem aus NP in polynomieller Zeit auf SAT zurückgeführt werden (Polynomialzeitreduktion). NP-vollständige Probleme stellen also eine Art obere Schranke für die Schwierigkeit von Problemen in NP dar.
Eine deterministische Turingmaschine (etwa ein konventioneller Computer) kann SAT in exponentieller Zeit entscheiden, zum Beispiel durch das Aufstellen einer Wahrheitstabelle. Es ist kein effizienter Algorithmus für SAT bekannt und es wird allgemein vermutet, dass ein solcher Polynomialzeitalgorithmus nicht existiert. Die Frage, ob SAT in polynomieller Zeit gelöst werden kann, ist äquivalent zum P-NP-Problem, einem der bekanntesten offenen Probleme der theoretischen Informatik
Ein Großteil der Forschung beschäftigt sich mit der Entwicklung möglichst effizienter Verfahren zur Lösung von SAT in der Praxis (sogenannter SAT-Solver). Moderne SAT-Solver können Instanzen mittlerer Schwierigkeit mit hunderten Millionen Variablen oder Klauseln in praktikabler Zeit lösen.[1] Das ist ausreichend für praktische Anwendungen, z. B. in der formalen Verifikation[2], in der künstlichen Intelligenz[3], in der Electronic Design Automation[4] und in verschiedene Planungs- und Schedulingalgorithmen[5].
Terminologie
Eine aussagenlogische Formel besteht aus Variablen, Klammern und den aussagenlogischen Verknüpfungen Konjunktion („und“, oft notiert mit ∧), Disjunktion („oder“, ∨) und Negation („nicht“, ¬). Eine Variable kann entweder den Wert wahr oder den Wert falsch annehmen. Ein Literal ist ein Auftreten einer Variable (positives Literal) oder ihrer Negation (negatives Literal). Ein Literal heißt pur, wenn es nur in einer Ausprägung, also entweder positiv oder negativ, vorkommt. Ein Monom ist eine endliche Menge von Literalen, die ausschließlich konjunktiv verknüpft sind. Eine Klausel ist eine endliche Menge von Literalen, die ausschließlich disjunktiv verknüpft sind. Eine Einheitsklausel ist eine Klausel, die nur aus einem einzelnen Literal besteht. Eine Horn-Klausel ist eine Klausel mit höchstens einem positiven Literal.
Eine aussagenlogische Formel ist in konjunktiver Normalform (KNF), wenn sie nur aus Konjunktionen von Klauseln besteht. Eine Horn-Formel ist eine konjunktive Normalform, die ausschließlich aus Horn-Klauseln besteht. Die Formel befindet sich in konjunktiver Normalform. Da nur die erste und die dritte Klausel Horn-Klauseln sind, ist sie aber keine Horn-Formel. Die dritte Klausel ist eine Einheitsklausel.
Eine aussagenlogische Formel ist in disjunktiver Normalform (DNF), wenn sie nur aus Disjunktionen von Monomen besteht. Die Formel befindet sich in disjunktiver Normalform.
Definition und Varianten
Eine Formel heißt genau dann erfüllbar, wenn eine Zuweisung von Werten wahr oder falsch zu jeder Variable existiert, sodass die Formel wahr ist. Formal ist SAT definiert als die formale Sprache
ist aussagenlogische Formel und erfüllbar
In der Praxis versteht man unter SAT meistens das Problem, herauszufinden ob eine Formel erfüllbar ist. Es existieren zahlreiche Varianten und für die meisten Komplexitätsklassen existiert eine Variante von SAT, die bezüglich dieser Klasse vollständig ist.
Polynomiell entscheidbare Varianten von SAT
- HORNSAT beschränkt SAT auf Horn-Formeln, das heißt auf Formeln in konjunktiver Normalform bei der jede Klausel höchstens ein positives Literal enthält. HORNSAT ist P-vollständig und in Linearzeit entscheidbar.[6]
- DNF-SAT beschränkt SAT auf Formeln, die in disjunktiver Normalform gegeben sind. DNF-SAT ist in polynomieller Zeit entscheidbar, da eine in DNF gegebene Formel genau dann erfüllbar ist, wenn es ein Monom gibt das keine komplementären Literale enthält.
- 2-SAT beschränkt SAT auf Formeln, deren Klauseln maximal 2 Literale enthalten. 2-SAT ist in Linearzeit entscheidbar.[7]
3-SAT
Das Problem 3-SAT schränkt die Anzahl Literale auf 3 Literale pro Klausel ein. Trotz dieser Einschränkung ist 3-SAT NP-vollständig, da SAT sich in polynomieller Zeit auf 3-SAT reduzieren lässt. Dasselbe gilt für alle Probleme k-SAT mit k > 3.
P3-SAT
Eine Instanz des Problems 3-SAT, bestehend aus p Variablen und q Klauseln, lässt sich auch mittels eines Graphen mit (p + q) vielen Knoten darstellen. Eine Formel ist in P3-SAT, wenn sie in 3-SAT ist und dieser Graph planar ist. P3-SAT ist NP-vollständig.
MAX-SAT und MAJ-SAT
Das Problem MAX-SAT besteht darin, die maximale Anzahl erfüllbarer Klauseln einer gegebenen Formel zu bestimmen. MAX-SAT ist NP-vollständig und sogar APX-vollständig. Daraus folgt, dass kein PTAS für MAX-SAT existieren kann, falls P ≠ NP.[8]
MAJ-SAT
MAJ-SAT ist das Problem zu entscheiden, ob die Mehrzahl aller möglichen Variablenbelegungen die Formel erfüllt. MAJ-SAT ist PP-vollständig.[9]
Algorithmen
Da SAT NP-vollständig ist, sind ausschließlich Exponentialzeitalgorithmen für SAT bekannt. Seit den 2000er-Jahren werden aber effiziente und skalierbare Algorithmen (SAT-Solver) entwickelt, die praktikables SAT-Solving für zahlreiche Anwendungen erlauben. Beispiele für Anwendungen sind formale Verifikation[2], künstlichen Intelligenz[3], Electronic Design Automation[4] und verschiedene Planungs- und Schedulingalgorithmen[5].
SAT-Solver können aufgrund ihrer Funktionsweise in verschiedene Klassen eingeteilt werden.
Backtracking und DPLL
Der Davis-Putnam-Logemann-Loveland-Algorithmus (DPLL oder DLL) aus den 1960er-Jahren war der erste SAT-Solver, der eine systematische Suche mittels Backtracking implementierte.[10][11] Er ist nicht zu verwechseln mit dem Davis-Putnam-Algorithmus, auf dem er basiert. Viele moderne Ansätze basieren auf dem gleichen Konzept und optimieren oft lediglich die Effizienz des Algorithmus für bestimmte Klassen von Eingaben, wie z. B. zufällige SAT-Instanzen oder Instanzen, die in Anwendungen der Industrie auftreten.[12] DPLL löst das CNF-SAT-Problem. Das bedeutet, die aussagenlogischen Formeln müssen in der konjunktiven Normalform vorliegen (Menge von Klauseln).
Ein grundlegender Backtracking-Algorithmus für eine Formel funktioniert wie folgt:
- Wähle ein Literal aus .
- Weise einen Wahrheitswert wahr oder falsch zu.
- Vereinfache zu , indem alle Klauseln entfernt werden, die nun wahr sind und alle Literale entfernt werden, die nun falsch sind.
- Splitting Rule. Prüfe rekursiv, ob erfüllbar ist.
- ist erfüllbar ist erfüllbar.
- ist nicht erfüllbar: Weise den komplementären Wahrheitswert zu. Vereinfache und prüfe dann erneut rekursiv, ob die resultierende Formel erfüllbar ist. Ist erfüllbar, so ist auch erfüllbar. Ist nicht erfüllbar, so ist auch nicht erfüllbar.
Der Algorithmus terminiert, wenn eine Klausel leer wird (nicht erfüllbar, ihr letztes Literal wurde falsch) oder wenn alle Variablen belegt sind (erfüllbar).
DPLL verbessert den simplen Backtracking-Algorithmus durch zwei Regeln.
Einheitsresolution (Unit Propagation)
Tritt eine Einheitsklausel auf, so muss ihr einziges Literal wahr sein. Weise dem Literal den entsprechenden Wahrheitswert zu und entferne alle Klauseln, die enthalten. Entferne Vorkommen des Literals aus allen Klauseln.
In der Praxis führt Einheitsresolution oft dazu, dass wiederum Einheitsklauseln erzeugt werden und somit der naive Suchraum signifikant verkleinert wird.
Pure Literal Elimination
Kommt ein Literal als pures Literal vor, so kann ihm ein Wert zugewiesen werden, sodass alle Klauseln, die das Literal enthalten, wahr werden. Entferne diese Klauseln.
Der Algorithmus zusammengefasst im Pseudocode:
function DPLL(F : set of clauses)
# Konsistent bedeutet, es kommt ausschließlich ¬l oder l vor
if F is a consistent set of literals then
# Hier können zusätzlich die Literale zurückgegeben werden
return true;
if F contains an empty clause then
return false;
for every unit clause {l} in F do
F ← unit-propagate(l, F);
for every literal l that occurs pure in F do
F ← pure-literal-assign(l, F);
l ← choose-literal(F);
# Mit Kurzschlussauswertung für das Oder return DPLL({F : l = true}) or DPLL({F : l = true}); #
Dabei wenden unit-propagate(l, F) und pure-literal-assign(l, F) die beiden Regeln entsprechend an und geben die vereinfachte Formel zurück.
Die Effizienz von DPLL hängt sehr stark von der Auswahl des Literals (Branching Literal) ab. Für manche Instanzen kann diese Wahl den Unterschied zwischen konstanter und exponentieller Laufzeit ausmachen.[13] Darum definiert DPLL vielmehr eine ganze Familie von Algorithmen, die unterschiedliche Heuristiken für die Wahl von verwenden.
Die Probleme von DPLL können in drei Punkten zusammengefasst werden:
- Die Entscheidungen für Branching Literals werden naiv getroffen.
- Aus Konflikten wird nichts gelernt, außer dass die aktuelle (partielle) Variablenbelegung zu einem Konflikt führt. Dabei lassen sich mehr Informationen über die Ursache des Konfliktes extrahieren und so große Teile des Suchraumes ausschließen.
- Backtracking springt nur jeweils eine Ebene im Suchbaum nach oben, was zu einem sehr großen Suchraum führt.
In der Praxis werden diese Probleme gelöst durch
- Heuristiken, z. B. in einem Look-Ahead-Solver
- Clause Learning (CDCL)
- Backjumping (CDCL)
Conflict-Driven Clause Learning (CDCL)
Modernes Conflict-driven Clause Learning (CDCL) erweitert DPLL um die Konzepte Clause Learning und Backjumping, implementiert Two Watched Literals (TWL, 2WL), um die Suche nach Einheitsklauseln zu beschleunigen und verwendet Random Restarts, um schwierigen Situationen nach eine Reihe von schlechten Entscheidungen für Variablenbelegungen zu entfliehen.
Backjumping und Clause Learning
Bei CDCL findet das Backtracking nicht mehr chronologisch statt, sondern es werden Ebenen des Suchbaumes übersprungen. Außerdem werden Informationen über Variablenbelegungen, die in Kombination einen Konflikt verursachen, als Klausel der Klauselmenge hinzugefügt.
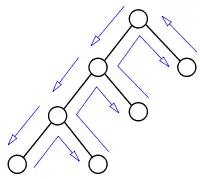 Backtracking ohne Backjumping
Backtracking ohne Backjumping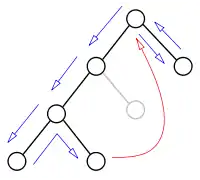 Backtracking mit Backjumping
Backtracking mit Backjumping
Um Backjumping zu ermöglichen merkt sich CDCL, welche Zuweisungen von Wahrheitswerten zu Variablen willkürlich waren und welche Zuweisungen durch Unit Propagation erzwungen wurden. In der Praxis funktioniert das mittels eines Implikationsgraphen.
Ein Implikationsgraph ist ein gerichteter, azyklischer Graph . Jeder Knoten besteht dabei aus einem Tupel oder einem Element . Während das Tupel für eine Zuweisung von wahr oder falsch für ein Literal auf Ebene des Suchbaumes steht, steht für einen aufgetretenen Konflikt. Ein Konflikt tritt auf, wenn ein Literal gleichzeitig den Wert wahr und den Wert falsch annehmen müsste.
Wenn der Algorithmus ein Literal willkürlich mit einem Wahrheitswert belegt, wird der entsprechende Knoten mit dem Tupel, das diese Zuweisung repräsentiert, zu hinzugefügt. Erzwingt diese Zuweisung durch Unit Propagation eine weiter Zuweisung, so wird ein weiterer Knoten und eine Kante zum Graphen hinzugefügt.
Im Folgenden ein Beispiel mit der Formel: ( ∨ ) ∧ ( ∨ ∨ ) ∧ ( ∨ ∨ ) ∧ ( ∨ ) ∧ ( ∨ ∨ ) ∧ ( ∨ ∨ ) ∧ ( ∨ ∨ ) ∧ ( ∨ ∨ )
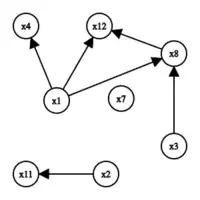 Implikationsgraph nach dem 8. Schritt
Implikationsgraph nach dem 8. Schritt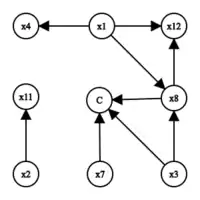 Implikationsgraph mit Konflikt
Implikationsgraph mit Konflikt
- Wähle willkürlich und belege es (wieder willkürlich) mit false.
- Unit Propagation erzwingt eine Belegung von mit true. Damit wird die Klausel ( ∨ ) wahr.
- Wähle und belege es mit true.
- Unit Propagation erzwingt nun die Belegung von mit false (wegen = false). Die Klausel ( ∨ ∨ ) wird wahr.
- Unit Propagation erzwingt die Belegung von mit true (wegen = false). Die Kausel ( ∨ ∨ ) wird wahr.
- Wähle und belege es mit false.
- Unit Propagation erzwingt nun die Belegung von mit true. Die Klausel ( ∨ ) wird wahr.
- Wähle und belege es mit true. Die Klauseln ( ∨ ∨ ) und ( ∨ ∨ ) werden wahr.
- Ein Konflikt tritt auf für . Unit Propagation muss die Klauseln ( ∨ ∨ ) ∧ ( ∨ ∨ ) erfüllen, die inzwischen zu ∧ reduziert wurden. Der Konfliktknoten wird in den Implikationsgraphen eingefügt.
Der Algorithmus analysiert nun den Konflikt mithilfe des Implikationsgraphen und entscheidet, welche Klausel gelernt werden soll und zu welchem Entscheidungslevel im Suchbaum zurückgesprungen werden soll. In Frage kommende Klauseln heißen conflict clause und sollen verhindern, dass die Fehlentscheidung des Algorithmus, die zum Konflikt geführt hat, wiederholt wird. Eine solche conflict clause wird zur Klauselmenge hinzugefügt. Das maximale Entscheidungslevel der Variablen aus der conflict clause bestimmt das Entscheidungslevel für das Backjumping.
Eine abstrakte Beschreibung von CDCL im Pseudocode sieht wie folgt aus:[14]
function CDCL(F : set of clauses)
G <- Implikationsgraph();
if unit-propagate(F, G) findet Konflikt then
return false;
level ← 0;
while F hat nicht zugewiesene Variablen do
level ← level + 1;
choose-literal(F, G);
while unit-propagate(F, G) findet Konflikt do
# Ermittle Ebene für Backjump und zu lernende Klausel
(d, c) ← analyzeConflict(G);
# Lerne
F ← F ∪ {c};
# Wenn der Konflikt nicht aufgelöst werden kann
if d < 0 then
return false;
else
backjump(F, d);
level ← d;
return true;
Dabei aktualisieren unit-propagate(F, G) und choose-literal(F, G) jeweils entsprechend den Implikationsgraphen. Die Funktion analyzeConflict(G) wird durch die Strategie des clause learning bestimmt.
Conflict Clauses
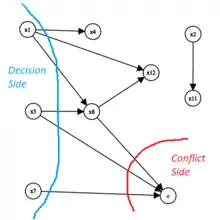
Um eine conflict clause zu ermitteln untersucht man Schnitte im Implikationsgraphen. Ein Schnitt generiert eine conflict clause genau dann, wenn er den Graph so in zwei Hälften partitioniert, dass eine Hälfte (die decision side) alle decision nodes enthält und die andere Hälfte den Konfliktknoten. Die decision nodes sind dabei die willkürlichen Entscheidungen, die zum Konflikt geführt haben.
Aus dem Implikationsgraphen wird ersichtlich, dass z. B. für und eine willkürliche Entscheidung getroffen wurde, aber die Entscheidung für die Belegung von eine Konsequenz aus der Entscheidung für die Belegung von und war. Die Knoten für , , sind also die decision nodes.
Ein Beispiel für einen Schnitt, der eine conflict clause generiert, ist ein Schnitt durch die eingehenden Kanten den Konfliktknotens (roter Schnitt in der Abbildung). Die Knoten auf der decision side repräsentieren die Ursache des Konfliktes, nämlich . Durch Kontraposition erhält man , ein Beispiel für eine conflict clause. Eine andere Möglichkeit stellt der blaue Schnitt durch die ausgehenden Kanten der decision nodes dar. Er generiert die conflict clause . Diese Variante wurde in Rel_sat[15] implementiert, einem der ersten CDCL SAT-Solver.[16] Eine fortgeschrittene Variante wird von der Implementierung GRASP[17] eingesetzt.
Two Watched Literals (TWL, 2WL)
Es bleibt das Problem, Einheitsklauseln für die Unit Propagation und Konflikte effizient zu finden. Lange Zeit haben Solver dafür die Anzahl Literale, die in einer Klausel noch nicht mit Wahrheitswerten belegt worden sind, mitgezählt. Wenn sich dieser Zähler von 2 auf 1 ändert wendet man Unit Propagation an. Da uns der genau Wert des Zählers aber eigentlich nicht interessiert, sondern wir nur wissen müssen, wann sich die Zahl auf eins ändert, verfolgen wir nicht die Klauseln selbst, sondern jeweils zwei Literale pro Klausel – die two watched literals. TWL ist also eine Datenstruktur, die die Suche nach Konflikten oder Einheitsklauseln beschleunigt.
Jeder Klausel, die noch nicht erfüllt ist, besitzt zwei watched literals. Die Information wird dabei nicht von den Klauseln gespeichert, sondern von den Literalen selbst. Jeder Literal besitzt also eine Liste mit Klauseln, in denen er vorkommt. Diese Klauseln werden in einer Liste verkettet, der watch list.
Die TWL einer Klausel erfüllen folgende Invariante:
„Solange kein Konflikt gefunden wurde darf ein watched literal nur false sein, solange der andere watched literal true ist und alle unwatched literals false sind.“[18]
Die Invariante führt dazu, dass die Belegung eines unwatched literals mit einem Wahrheitswert niemals zu einer unit propagation oder einem Konflikt führen wird. Wenn wir nun aber einem watched literal einen Wahrheitswert zuweisen müssen wir eventuell die Invariante reparieren, unit propagation anwenden oder einen Konflikt auflösen. Betrachten wir die Klauseln, in denen die Negation von , also vorkommt. Diese können durch die watch list effizient gefunden werden. Wir verfahren für diese wie folgt:
- Ist der andere watched literal der Klausel true, müssen wir nichts tun.
- Ist einer der unwatched literals der Klausel nicht false, wählen wir als watched literal, der ersetzt.
- Ist der andere watched literal für diese Klausel noch nicht mit einem Wahrheitswert belegt, führe unit propagation für durch. Ansonsten ist false und ein Konflikt wurde gefunden.
TWL wurde für den SAT-Solver Chaff[19] entwickelt, um die unit propagation in der Praxis zu optimieren.
Random Restart
Random Restarts setzen alle Variablenbelegungen zurück und starten die Suche mit einer anderen Reihenfolge der Variablenbelegung neu. Damit wird das Problem umgangen, dass manche dieser Zuweisungsreihenfolgen zu sehr viel länger andauernden Berechnungen mit vielen Konflikten führen, während geeignete Reihenfolgen das Problem schneller lösen. Dabei werden gelernte Klauseln und die aktuell zugewiesenen Werte der Variablen übernommen. Wann ein Restart durchgeführt wird bestimmt eine Strategie, z. B. fixed nach n Konflikten, in Abständen, die einer Reihe wie der geometrischen Reihe folgen oder dynamisch, wenn sich Konflikte beginnen zu häufen. Restart-Strategien sind häufig an eine bestimmte Klasse von Instanzen angepasst und aggressivere Strategien haben sich in vielen Fällen als effizient herausgestellt.[20]
Lokale Suche
SAT-Solver, die auf dem Prinzip der lokalen Suche basieren, führen im Grunde folgende Schritte aus:
- Weise jeder Variable einen Zufallswert true oder false zu.
- Wenn alle Klauseln erfüllt sind, terminiere und gebe die Variablenbelegung zurück.
- Ansonsten negiere eine Variable und wiederhole.
Die aussagenlogische Formel ist dabei als konjunktive Normalform gegeben. Unterschiede zwischen SAT-Solvern, die lokale Suche implementieren, finden sich vor allem bei der Wahl der Variable, die negiert wird.
GSAT[21] negiert die Variable, die die Zahl an nicht erfüllten Klauseln minimiert oder wählt mit einer gewissen Wahrscheinlichkeit eine zufällige Variable.
WalkSAT[22] wählt eine zufällige, nicht erfüllte Klausel und negiert eine Variable. Dabei wird die Variable ausgewählt, die am wenigsten bereits erfüllte Klauseln nicht erfüllt werden lässt. Die Wahrscheinlichkeit, dass eine falsche Variablenzuweisung korrigiert wird, ist der Kehrwert der Anzahl der Variablen in der Klausel. Mit einer gewissen Wahrscheinlichkeit wird auch hier einfach eine zufällige Variable der Klausel ausgewählt.
Beide Varianten erlauben zufällige Zuweisungen mit einer gewissen Wahrscheinlichkeit, um das Problem der lokalen Maxima zu umgehen. Außerdem werden zufällige Neustarts erlaubt, wenn für eine zu lange Zeit keine Lösung gefunden wurde.
Parallelisierung
Parallele SAT-Solver können in drei Kategorien eingeteilt werden: Portfolio, Divide-and-conquer und parallele lokale Suche.
Portfolio
Portfolio SAT-Solver beruhen auf der Tatsache, dass die meisten SAT-Solver auf bestimmten Probleminstanzen effizient sind, aber auf anderen Instanzen langsamer sind als andere Algorithmen. Gegeben eine beliebige Instanz von SAT, so gibt es keine verlässliche Möglichkeit, um vorherzusagen, welcher Algorithmus die Instanz am schnellsten lösen wird. Der Portfolio-Ansatz verwendet nun verschiedene Ansätze parallel, um die Vorteile verschiedener SAT-Solver zu kombinieren. Ein Nachteil der Methode ist natürlich, dass alle parallele Prozesse im Prinzip die gleiche Arbeit verrichten. Trotzdem haben sich Portfolio-Solver in der Praxis als effizient herausgestellt.
Cube-And-Conquer
Divide-and-conquer Algorithmen beruhen auf dem Ansatz, ein Problem in kleinere Teilprobleme aufzuteilen, diese rekursiv zu bearbeiten und die Teilergebnisse zu kombinieren. DPLL und CDCL sind divide-and-conquer Algorithmen, die den Suchraum bei der jeder Entscheidung für eine Variablenbelegung in zwei Hälften aufteilen. Durch unit propagation und pure literal elimination können diese Hälften aber sehr unterschiedlich schwer zu lösende Teilinstanzen von SAT darstellen. CDCL verschärft dieses Problem durch die Anwendung weiteren Techniken. Cube-and-conquer ist ein Ansatz, der dieses Problem in zwei Phasen löst.
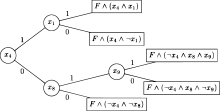
- Cube Phase. Die Instanz von SAT wird von einem SAT-Solver in viele (einige Tausend bis einige Millionen) Teilprobleme aufgeteilt, sogenannte Würfel. Ein Würfel ist dabei eine Konjunktion einer Teilmenge der Literale des Originalformel F.
- Konjunktiv mit F verknüpft ergibt sich eine neue Formel F', die unabhängig von den anderen Teilproblemen gelöst werden kann (z. B. CDCL). Die Disjunktion aller F' ist äquivalent zu F. Der Algorithmus terminiert also, sobald ein Teilproblem erfüllbar ist.
Für die Cube Phase wird in der Regel ein Look-Ahead-Solver eingesetzt, da diese sich für kleine, aber schwere Probleme bewährt haben und globaler arbeiten als z. B. CDCL.[23]
Parallele lokale Suche
Parallele lokale Suche ist leicht zu parallelisieren: Flips von verschiedenen Variablen werden parallel durchgeführt oder ein Portfolio-Ansatz wird verwendet, indem unterschiedliche Strategien für die Variablenauswahl gleichzeitig angewandt werden.
Praxis
Die SAT-Competition ist ein Wettbewerb[24] für SAT-Solver, der jährlich im Rahmen der International Conference on Theory and Applications of Satisfiability Testing stattfindet.[25] In verschiedenen Disziplinen werden unterschiedliche Qualitäten von SAT-Solvern evaluiert:
- Sequentielle Performance (teilweise existieren separate Wettbewerbe für bestimmte Klassen von Instanzen, z. B. Instanzen aus dem Automated Planning)
- Mäßige Parallelisierung auf einer einzelnen Maschine mit Shared Memory
- Massive Parallelisierung auf verteilten Maschinen
- Inkrementelle SAT-Solver, also SAT-Solving für Anwendungen, die mehrere Lösungsschritte benötigen. Dabei wird eine Sequenz verwandter SAT-Instanzen gelöst, wobei bereits gelernte Informationen aus früheren Instanzen wiederverwendet werden.[26]
Die SAT-Association ist eine Vereinigung, die sich zum Ziel gesetzt hat, Forschung im Bereich SAT, SAT-Solver und der formalen Verifikation voranzubringen und die SAT-Community zu repräsentieren.[27] Sie beaufsichtigt die Organisation der genannten Konferenzen und Wettbewerbe und gibt das Journal on Satisfiability, Boolean Modeling, and Computation (JSAT) heraus.[28]
Siehe auch
Einzelnachweise
- SAT Competition 2020. Abgerufen am 9. November 2020.
- Randal E. Bryant, Steven German, Miroslav N. Velev: Microprocessor Verification Using Efficient Decision Procedures for a Logic of Equality with Uninterpreted Functions. In: Lecture Notes in Computer Science. Springer Berlin Heidelberg, Berlin, Heidelberg 1999, ISBN 3-540-66086-0, S. 1–13.
- Henry Kautz, Bart Selman: Planning as satisfiability. In: Proceedings of the 10th European conference on Artificial intelligence (= ECAI '92). John Wiley & Sons, Inc., Vienna, Austria 1992, ISBN 0-471-93608-1, S. 359–363, doi:10.5555/145448.146725.
- João P. Marques-Silva, Karem A. Sakallah: Boolean satisfiability in electronic design automation. In: Proceedings of the 37th Annual Design Automation Conference (= DAC '00). Association for Computing Machinery, Los Angeles, California, USA 2000, ISBN 1-58113-187-9, S. 675–680, doi:10.1145/337292.337611.
- Hong Huang, Shaohua Zhou: An efficient SAT algorithm for complex job-shop scheduling. In: Proceedings of the 2018 8th International Conference on Manufacturing Science and Engineering (ICMSE 2018). Atlantis Press, Paris, France 2018, ISBN 978-94-6252-502-3, doi:10.2991/icmse-18.2018.126.
- William F. Dowling, Jean H. Gallier: Linear-time algorithms for testing the satisfiability of propositional horn formulae. In: The Journal of Logic Programming. Band 1, Nr. 3, 1984, S. 267–284, doi:10.1016/0743-1066(84)90014-1.
- Bengt Aspvall, Michael F. Plass, Robert Endre Tarjan: A linear-time algorithm for testing the truth of certain quantified boolean formulas. In: Information Processing Letters. Band 8, Nr. 3, März 1979, S. 121–123, doi:10.1016/0020-0190(79)90002-4.
- Christos Papadimitriou: Computational Complexity. Addison-Wesley, 1994.
- Pierluigi Crescenzi, Daniel Pierre Bovet: Introduction to the theory of complexity. Prentice Hall, New York 1994, ISBN 0-13-915380-2.
- Martin Davis, Hilary Putnam: A Computing Procedure for Quantification Theory. In: Journal of the ACM. Band 7, Nr. 3, Juli 1960, ISSN 0004-5411, S. 201–215, doi:10.1145/321033.321034.
- Martin Davis, George Logemann, Donald Loveland: A machine program for theorem-proving. In: Communications of the ACM. Band 5, Nr. 7, Juli 1962, ISSN 0001-0782, S. 394–397, doi:10.1145/368273.368557.
- Lintao Zhang, Sharad Malik: The Quest for Efficient Boolean Satisfiability Solvers. In: Computer Aided Verification. Band 2404. Springer Berlin Heidelberg, Berlin, Heidelberg 2002, ISBN 3-540-43997-8, S. 17–36, doi:10.1007/3-540-45657-0_2.
- João Marques-Silva: The Impact of Branching Heuristics in Propositional Satisfiability Algorithms. In: Progress in Artificial Intelligence. Band 1695. Springer Berlin Heidelberg, Berlin, Heidelberg 1999, ISBN 3-540-66548-X, S. 62–74, doi:10.1007/3-540-48159-1_5.
- Emina Torlak: A Modern SAT Solver Lecture, University of Washington. (PDF) Abgerufen am 8. November 2020 (englisch).
- Roberto J. Bayardo, Robert Schrag: Using CSP look-back techniques to solve exceptionally hard SAT instances. In: Lecture Notes in Computer Science. Springer Berlin Heidelberg, Berlin, Heidelberg 1996, ISBN 3-540-61551-2, S. 46–60.
- Lintao Zhang, S. Malik: Conflict driven learning in a quantified Boolean satisfiability solver. In: IEEE/ACM International Conference on Computer Aided Design. IEEE, 2002, ISBN 0-7803-7607-2, doi:10.1109/iccad.2002.1167570.
- J.P. Marques-Silva, K.A. Sakallah: GRASP: a search algorithm for propositional satisfiability. In: IEEE Transactions on Computers. Band 48, Nr. 5, Mai 1999, S. 506–521, doi:10.1109/12.769433.
- Mathias Fleury, Jasmin Christian Blanchette, Peter Lammich: A verified SAT solver with watched literals using imperative HOL. In: Proceedings of the 7th ACM SIGPLAN International Conference on Certified Programs and Proofs - CPP 2018. ACM Press, New York, New York, USA 2018, ISBN 978-1-4503-5586-5, doi:10.1145/3167080.
- Matthew W. Moskewicz, Conor F. Madigan, Ying Zhao, Lintao Zhang, Sharad Malik: Chaff: engineering an efficient SAT solver. In: Proceedings of the 38th conference on Design automation - DAC '01. ACM Press, Las Vegas, Nevada, United States 2001, ISBN 1-58113-297-2, S. 530–535, doi:10.1145/378239.379017.
- Gilles Audemard, Laurent Simon: Predicting Learnt Clauses Quality in Modern SAT Solvers. In: Proceedings of the 21st International Joint Conference on Artificial Intelligence (IJCAI). 2009.
- B. Selman, H. J. Levesque, and D. G. Mitchell: A new method for solving hard satisfiability problems. 10th AAAI. San Jose, CA 1992, S. 440–446.
- K Keefe: Local search strategies for equational satisfiability. Office of Scientific and Technical Information (OSTI), 21. September 2004.
- Marijn J.H. Heule and Hans van Maaren: Look-Ahead Based SAT Solvers, Handbook of Satisfiability. Hrsg.: IOS Press. EasyChair, 2009, doi:10.29007/g7ss (utexas.edu [PDF; abgerufen am 8. November 2020]).
- The International SAT Competition Web Page
- The International Conferences on Theory and Applications of Satisfiability Testing (SAT)
- Katalin Fazekas, Armin Biere, Christoph Scholl: Incremental Inprocessing in SAT Solving. In: Theory and Applications of Satisfiability Testing – SAT 2019 (= Lecture Notes in Computer Science). Springer International Publishing, Cham 2019, ISBN 978-3-03024258-9, S. 136–154, doi:10.1007/978-3-030-24258-9_9.
- The SAT Association
- Journal on Satisfiability, Boolean Modeling and Computation ISSN 1574-0617