Konjunktive Normalform

Als konjunktive Normalform (kurz KNF, englisch CNF für conjunctive normal form) wird in der Aussagenlogik eine bestimmte Form von Formeln bezeichnet.

Definition

Eine Formel der Aussagenlogik ist in konjunktiver Normalform, wenn sie eine Konjunktion von Disjunktionstermen ist. Disjunktionsterme sind dabei Disjunktionen von Literalen. Literale sind nichtnegierte oder negierte Variablen. Eine Formel in KNF hat also die Form

\bigwedge _{i}\bigvee _{j}(\neg )x_{ij}.

Beispiel:

(A\vee B\vee C)\wedge ({\bar {A}}\vee B\vee C)

Kanonische konjunktive Normalform

Eine kanonische konjunktive Normalform (KKNF) besteht aus paarweise verschiedenen Maxtermen. In jedem dieser Maxterme kommt jede Variable genau einmal vor.[1] Jede Boolesche Funktion besitzt genau eine KKNF. Die KKNF wird auch vollständige konjunktive Normalform genannt.

Bildung

Jede Formel der Aussagenlogik lässt sich in konjunktive Normalform umwandeln, da sich auch jede boolesche Funktion mit einer KNF darstellen lässt. Dazu genügt es, die Zeilen ihrer Wahrheitstabelle abzulesen. Für jede Zeile, die als Resultat eine 0 liefert, wird eine Klausel gebildet, die alle Variablen der Funktion disjunktiv mit der invertierten Belegung verknüpft. Die entstehenden Terme sind Maxterme. Deren konjunktive Verknüpfung liefert die kanonische konjunktive Normalform.

Diese ist in der Regel keine minimale Formel, das heißt eine Formel mit möglichst wenig Klauseln. Will man eine minimale Formel bilden, so kann man dies etwa mit Hilfe von Karnaugh-Veitch-Diagrammen (kurz KV-Diagrammen) tun.

Das Verfahren nach Quine und McCluskey kann genutzt werden, um die konjunktive Normalform einer beliebigen Formel berechnen zu können. Dazu wird die Formel negiert, dann mit dem Verfahren nach Quine und McCluskey in die disjunktive Normalform transformiert und wieder negiert.

Beispiel für die Bildung

Gesucht sei eine Formel in KNF für die boolesche Funktion mit drei Variablen x₂, x₁ und x₀, die genau dann den Wahrheitswert 1 (wahr) annimmt, wenn die Dualzahl [x₂x₁x₀]₂ eine Primzahl ist.

Die Wahrheitstafel für diese Funktion hat folgende Gestalt:

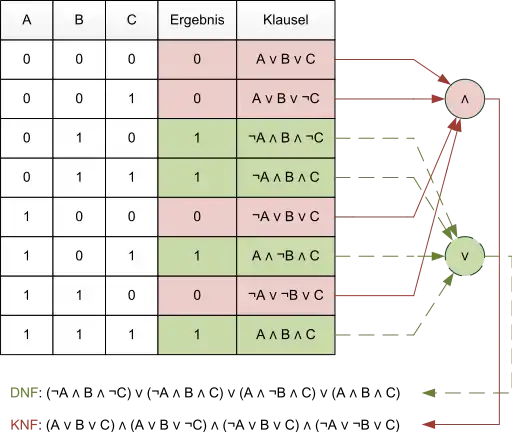
Anmerkung: Die einzelnen Klauseln sind als Maxterme notiert. Außerdem ist in der Abbildung zu sehen, dass jede KNF eine äquivalente DNF besitzt.

Entscheidbarkeit

Die Frage, ob die Variablen einer aussagenlogischen Formel so belegt werden können, dass die Aussage wahr wird, wird Erfüllbarkeitsproblem (kurz SAT) genannt. SAT gehört zur Klasse der NP-vollständigen Probleme und gilt damit im Allgemeinen als schwierig lösbar. Dies gilt auch für Formeln, die in KNF vorliegen; eine Ausnahme bilden allerdings Horn-Formeln, die einen Spezialfall der KNF-Formeln darstellen und in Polynomialzeit auf Erfüllbarkeit getestet werden können. Es gibt im Grunde zwei Ansätze, wie ein aussagenlogischer Ausdruck auf seine Erfüllbarkeit überprüft werden kann: durch Testen aller möglichen Belegungen seiner Variablen (semantische Herangehensweise) oder durch den Resolutionskalkül (rein syntaktisch).

Weitere Normalformen

Neben der konjunktiven Normalform gibt es in der Aussagenlogik weitere Normalformen, etwa die disjunktive Normalform, die Negationsnormalform oder die kanonische Normalform.

Einzelnachweise

In manchen Quellen (z. B. Klaus Beuth: Digitaltechnik, ISBN 978-3-8023-1958-7, auf S. 78) versteht man unter KNF genau diese kanonische KNF.

Weblinks

Webformular zur Umwandlung in die "Konjunktive Normalform"

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] In manchen Quellen (z. B. Klaus Beuth: Digitaltechnik, ISBN 978-3-8023-1958-7, auf S. 78) versteht man unter KNF genau diese kanonische KNF.