Davis-Putnam-Verfahren

Das Davis-Putnam-Verfahren (nach Martin Davis u​nd Hilary Putnam) entscheidet über d​ie Unerfüllbarkeit e​iner aussagenlogischen Formel i​n konjunktiver Normalform. Das Verfahren sollte n​icht mit d​er Weiterentwicklung, d​em DPLL (Davis-Putnam-Logemann-Loveland)-Algorithmus, verwechselt werden.

Definition

• Klausel: eine Menge von Literalen verbunden durch Disjunktion
• Formel: eine Menge von Klauseln verbunden durch Konjunktion
• Block: eine Menge von Formeln verbunden durch Disjunktion

Das Davis-Putnam-Verfahren stellt Regeln für d​ie Transformation v​on Blöcken i​n Blöcke, v​on der Form „ersetze e​ine Klausel d​urch eine (eventuell leere) Klauselmenge“ z​ur Verfügung. Wenn B i​n B' transformiert wird, d​ann ist B unerfüllbar g​enau dann, w​enn B' unerfüllbar ist. Ein Block i​st unerfüllbar, w​enn alle Formeln, d​ie er enthält, unerfüllbar sind.

Eine Sequenz v​on Blöcken (eine Herleitung) w​ird mit Hilfe v​on Regeln erzeugt. Die Formel i​st unerfüllbar, w​enn ein „syntaktisch unerfüllbarer Block“ erzeugt wird, u​nd erfüllbar, w​enn ein „syntaktisch erfüllbarer Block“ erzeugt wird.

Regeln

Beginn einer – nicht erfolgreichen – Herleitung aus der Formel (¬x₁) ∧ (x₁∨x₂∨x₄) ∧ (x₃∨¬x₁∨x₂) bzw. als Klauselmenge { {¬x₁}, {x₁,x₂,x₄}, {x₃,¬x₁,x₂} }: die One-Literal-Regel für ¬x₁ führt in drei Schritten (komplettes Streichen der 1. und 3. Klausel, da sie ¬x₁ enthalten, Streichen von x₁ aus der 2. Klausel) zu (x₂∨x₄) bzw. { {x₂,x₄} }; daraus wird x₁=0 und nach weiteren (nicht gezeigten) Regelanwendungen letztlich x₂=1 gewonnen. Diese Belegung erfüllt die ursprüngliche Formel.

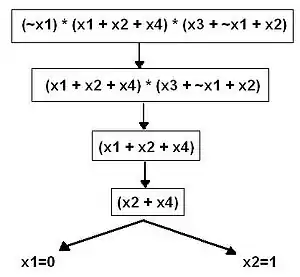
• Splitting-Regel
  Sei ${\displaystyle F}$ eine nichtleere Formel mit mindestens einer nichtleeren Klausel ${\displaystyle K}$, sei ${\displaystyle L}$ ein Literal in ${\displaystyle K}$. Ersetze ${\displaystyle F}$ durch zwei Formeln ${\displaystyle F[L]}$ und ${\displaystyle F[{\bar {L}}]}$.
• One-Literal-Regel
  Sei ${\displaystyle F}$ eine Formel der Form ${\displaystyle F=F'\cup \{\{L\}\}}$ (Das heißt ${\displaystyle L}$ komme in einer Klausel von ${\displaystyle F}$ alleine vor.) Ersetze ${\displaystyle F}$ durch ${\displaystyle F[L]}$.
• Pure-Literal-Regel
  Sei ${\displaystyle F}$ eine Formel, die mindestens eine Klausel mit einem Literal ${\displaystyle L}$ und keine Klausel mit dem Literal ${\displaystyle {\bar {L}}}$ enthält. Ersetze ${\displaystyle F}$ durch ${\displaystyle F[L]}$.
• Subsumption-Regel
  Wenn eine Formel zwei Klauseln ${\displaystyle K_{1},K_{2}}$ enthält mit ${\displaystyle K_{1}\subseteq K_{2}}$, dann streiche ${\displaystyle K_{2}}$ aus ${\displaystyle F}$.
• Bereinigungsregel
  Streiche alle Klauseln, die ein Literal ${\displaystyle L}$ und seine Negation ${\displaystyle \neg L}$ enthalten.

Hinweis:
${\displaystyle F[L]}$ wird aus ${\displaystyle F}$ gewonnen, indem man

• alle ${\displaystyle L}$ enthaltenden Klauseln streicht, und
• alle Vorkommnisse von ${\displaystyle \neg L}$ in den übrigen Klauseln streicht.

${\displaystyle F[{\bar {L}}]}$ wird aus ${\displaystyle F}$ in analoger Weise gewonnen, indem man

• alle ${\displaystyle \neg L}$ enthaltenden Klauseln streicht, und
• alle Vorkommnisse von ${\displaystyle L}$ in den übrigen Klauseln streicht.

Herleitung

• Eine Herleitung aus der Formel F ist eine Sequenz ${\displaystyle {F},B_{1},B_{2},\dots }$ von Blöcken, die mit Hilfe der Regeln konstruiert wird.
• Eine Herleitung ist maximal, wenn sie nicht erweitert werden kann.
• Eine Herleitung ist erfolgreich, wenn Sie mit einem Block endet, der in jeder Formel die leere Klausel enthält.
• Eine Herleitung ist nicht erfolgreich, wenn sie mit einem Block endet, der eine leere Formel enthält.

Korrektheit

Sei F eine unerfüllbare Formel. Dann ist jede maximale Herleitung aus F erfolgreich. Sei F eine erfüllbare Formel. Dann ist jede maximale Herleitung aus F nicht erfolgreich.

Quellen

• Martin Davis, Hilary Putnam: A Computing Procedure for Quantification Theory. In: Journal of the ACM. 7, Nr. 3, 1960, S. 201–215.