Komplexitätsklasse
In der Komplexitätstheorie werden Probleme oder Algorithmen darauf untersucht, wie aufwendig sie zu berechnen sind bezüglich einer bestimmten Ressource, meist bezüglich des Zeitaufwands oder des (Speicher-)Platzaufwands. Bei Problemen wird dabei stets das „kostengünstigste“ Lösungsverfahren angenommen. Der Aufwand ist im Allgemeinen abhängig von der „Größe“ der Eingabe, wie viele Elemente sie umfasst. Abgeschätzt wird der asymptotische Aufwand, also für sehr viele Eingabeelemente. Dabei zeigt sich, dass die Probleme bzgl. ihres Aufwands Gruppen bilden, deren Aufwand für große Eingabemengen auf ähnliche Weise anwächst; diese Gruppen werden Komplexitätsklassen genannt. Eine Komplexitätsklasse ist eine Menge von Problemen, welche sich in einem bestimmten ressourcenbeschränkten Berechnungsmodell berechnen lassen.
Definiert wird eine Komplexitätsklasse durch eine obere Schranke für den Bedarf einer bestimmten Ressource unter Voraussetzung eines Berechnungsmodells. Die am häufigsten betrachteten Ressourcen sind die Anzahl der notwendigen Berechnungsschritte zur Lösung eines Problems (Zeitkomplexität) oder der Bedarf an Speicherplatz (Raum- oder Platzkomplexität). Gemessen wird der Ressourcenbedarf in der Regel durch sein asymptotisches Verhalten an der Obergrenze (dem worst case) in Abhängigkeit von der Länge der Eingabe (Problemgröße).
Auch andere Maße des Ressourcenbedarfs sind möglich, etwa der statistische Mittelwert über alle möglichen Eingaben. Dieses Maß ist jedoch formal nur schwer zu analysieren.
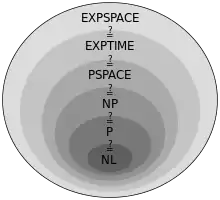
Da durch eine Komplexitätsklasse nur eine obere Grenze für den Ressourcenbedarf festgelegt ist, wird somit für ein gegebenes Berechnungsmodell eine Hierarchie von Komplexitätsklassen gebildet, wobei weniger mächtige Klassen jeweils vollständig in den jeweils höheren Komplexitätsklassen enthalten sind. Zudem können durch formale Methoden auch über unterschiedliche Berechnungsmodelle oder Ressourcen definierte Klassen zueinander in Bezug gesetzt werden.
Einteilung der Komplexitätsklassen
Die Komplexität wird häufig mit Hilfe der Landau-Symbole beschrieben, um von Eigenheiten bestimmter Implementierungen und Berechnungsmodelle zu abstrahieren. Die Schwierigkeit bei der Bestimmung der genauen Komplexität eines Problems liegt darin, dass man hierfür sämtliche mögliche Algorithmen betrachten müsste. Man muss also beweisen, dass ein bestimmter Algorithmus optimal für dieses Problem ist.
Die Komplexitätsklasse eines Algorithmus ist nur in einer konkreten Implementierung auf einer Maschine, z. B. auf einer Turingmaschine oder im Lambda-Kalkül feststellbar. Die Komplexitätsklassen der Implementationen eines Algorithmus auf unterschiedlichen Maschinenmodellen sind jedoch meistens ähnlich oder sogar – je nach Abstraktionslevel – gleich.
Es wird festgestellt, dass nur bestimmte Klassen dieser Größe sinnvoll unterscheidbar sind, die alle mit einer charakteristischen Gleichung beschrieben werden. So interessieren z. B. konstante Faktoren in der Komplexität eines Algorithmus nicht – schließlich gibt es in der Realität (Computer) auch Maschinen, deren Ausführungsgeschwindigkeit sich um einen konstanten Faktor unterscheidet. Hier wird auch klar, warum keine Einheiten gebraucht werden und wie die Landau-Notation zu verstehen ist.
Eine wichtige Rolle bei der Einteilung der Komplexitätsklassen spielt die Unterscheidung von Zeitkomplexität und Platzkomplexität, bei deren Betrachtung Zeit bzw. Platz beschränkt werden. Weiterhin unterscheidet man deterministische Maschinen von nichtdeterministischen. Informell lässt sich sagen, dass Platz mächtiger ist als Zeit und Nichtdeterminismus meistens mächtiger als Determinismus, allerdings jeweils nur exponentiell mächtiger. Genauere Abschätzungen hierzu geben der Satz von Savitch und der Satz von Immerman und Szelepcsényi.
Ein Problem A, das mit geringem Aufwand auf ein Problem B zurückgeführt (reduziert) werden kann, gehört mindestens zur Komplexitätsklasse von B. B wird dann schwerer als A genannt. Ein Problem A ist K-schwer, wenn sich alle anderen Probleme der Klasse K auf A zurückführen lassen. Liegt ein K-schweres Problem A selbst in der Klasse K, wird es K-vollständig genannt.[1]
Beispiel
- Rasenmähen hat mindestens lineare Komplexität (in der Fläche), denn man muss die gesamte Fläche mindestens einmal überfahren. Das heißt, der Zeitaufwand um m² Rasen zu mähen ist ( * Konstante) Sekunden. Für einen 3 Mal so großen Rasen braucht man 3 Mal so lange zum Mähen – der Zeitaufwand wächst linear.
- Einfache („dumme“) Sortierverfahren haben häufig eine quadratische Zeitkomplexität: braucht man für Bücher z. B. 15 Sekunden, um sie zu sortieren, so bräuchte man (mit diesem einfachen Verfahren) für 10 Mal so viele Bücher 100 Mal so lange, und für 50 Mal so viele Bücher dann 2500 Mal so viel Zeit – der Zeitaufwand steigt quadratisch.
- Suchen im Telefonbuch hat hingegen nur logarithmische Komplexität bei einer binären Suche, wenn man den jeweils verbliebenen Suchbereich immer in der Mitte aufschlägt, ob man zu weit vor oder hinter dem gesuchten Namen liegt.
Bei einem doppelt so dicken Telefonbuch schlägt man dieses nur ein Mal öfter auf, denn das halbiert den Suchbereich wieder auf das vorige Problem. Der Zeitaufwand, in Einträgen zu suchen, wächst dann mit . In doppelt so vielen Telefonnummern zu suchen, braucht nicht doppelt so viele Suchschritte, sondern nur genau einen zusätzlichen.
Siehe auch
Einzelnachweise
- Natalia Kliewer: Komplexitätstheorie. In: Lexikon der Wirtschaftsinformatik, Online-Lexikon, Oldenbourg Wissenschaftsverlag.