Disjunktive Normalform
Als disjunktive Normalform (kurz DNF) wird in der Booleschen Algebra eine in besonderer Weise normierte Funktionsdarstellung Boolescher Funktionen bezeichnet.
Definition
Eine Formel der Aussagenlogik ist in disjunktiver Normalform, wenn sie eine Disjunktion von Konjunktionstermen ist. Ein Konjunktionsterm wird ausschließlich durch die konjunktive Verknüpfung von Literalen gebildet. Literale sind dabei entweder nichtnegierte oder negierte Variablen. Eine Formel in DNF hat also die Form
Erläuterung
Bei der disjunktiven Normalform handelt es sich um einen logischen Ausdruck, der aus ODER-Verknüpfungen (Disjunktion – nicht ausschließendes ODER) besteht. Der logische Ausdruck besteht in der obersten Ebene ausschließlich aus ODER-Verknüpfungen.
Beispiel: A ODER B ODER C ODER D; A∨B∨C∨D
Dabei können die einzelnen Elemente der ODER-Verknüpfung (A, B, C, D) komplexere Ausdrücke sein, die dann auch eine oder mehrere UND-Verknüpfungen (Konjunktion) enthalten können.
Beispiel:
als formale Schreibweise:
Hier handelt es sich um eine Disjunktion (ODER-Verknüpfung) von drei Konjunktionen (UND-Verknüpfungen) und der Aussage D – genau das ist die disjunktive Normalform.
Vereinbarungsgemäß werden die Klammern und die Zeichen (Operatoren) für die UND-Verknüpfung nicht mitgeschrieben.
Beispiel:
Auch der NICHT-Operator kann in solchen Ausdrücken auftreten:
Beispiel:
Zusätzlich zu der bereits oben erwähnten Forderung, dass der logische Ausdruck in der obersten Ebene ausschließlich aus ODER-Verknüpfungen besteht (ODER-Ebene), darf es keine weiteren ODER-Verknüpfungen in tiefer geklammerten Ebenen geben. Nur zwei Ebenen sind zulässig: die obere Ebene der ODER-Verknüpfungen (ODER-Ebene) und die untere Ebene der UND-Verknüpfungen (UND-Ebene). Eine tiefere Verschachtelung gibt es nicht. Lediglich die Negation darf für die Elemente der UND-Ebene noch verwendet werden.
Das Ganze geht auch andersherum: eine UND-Verknüpfung von ODER-Aussagen und Einzelaussagen. Das ist die konjunktive Normalform (KNF) – das Gegenstück zur disjunktiven Normalform (DNF).
Praktischen Nutzen bringen solche Normalformen bei großen Aussagensystemen – beispielsweise bei der logischen Beschreibung der Flugzeugelektrik mit 50 Eingabeparametern und Hunderten von Kombinationsmöglichkeiten. Das System wird erst einmal von der wörtlichen Beschreibung in logische Formeln umgewandelt – z. B. „wenn der Fahrwerksensor die Landung meldet, darf die Schubumkehr aktiviert werden“. Diese Ansammlung von logischen Ausdrücken wird dann in die DNF umgewandelt. Dabei wird der logische Ausdruck in der Regel noch länger. In einem weiteren Schritt erfolgt eine Vereinfachung des logischen Ausdrucks mittels Karnaugh-Veitch-Diagramm oder dem Quine-McCluskey-Verfahren. Dabei werden logische Doppelungen entfernt und Überschneidungen berücksichtigt. Der letztendlich errechnete logische Ausdruck wird dann in die Steuersoftware integriert bzw. hardwaremäßig in der Steuerelektronik umgesetzt.
Bildung
Jede Formel der Aussagenlogik lässt sich in die disjunktive Normalform umwandeln, da sich auch jede Boolesche Funktion mit einer DNF darstellen lässt. Dazu genügt es, die Zeilen ihrer Wahrheitstabelle abzulesen. Für jede Zeile, die als Resultat eine 1 liefert, wird eine Konjunktion gebildet, die alle Variablen der Funktion (der Zeile) verknüpft. Variablen, die in der Zeile mit 1 belegt sind, werden dabei nicht negiert und Variablen, die mit 0 belegt sind, werden negiert. Diese Terme werden auch Minterme genannt. Durch disjunktive Verknüpfung der Minterme erhält man schließlich die disjunktive Normalform.
Auf diese Weise erhält man allerdings in der Regel keine minimale Formel, das heißt eine Formel mit möglichst wenig Termen. Will man eine minimale Formel bilden, so kann man dies mit Hilfe von Karnaugh-Veitch-Diagrammen oder mithilfe des Quine-McCluskey-Verfahrens tun.
Beispiel für die Bildung der DNF
Gesucht sei eine Formel in DNF für die Boolesche Funktion mit drei Variablen x2, x1 und x0, die genau dann den Wahrheitswert 1 (wahr) annimmt, wenn die Dualzahl [x2x1x0]2 eine Primzahl ist.
Die Wahrheitstafel für diese Funktion hat folgende Gestalt:
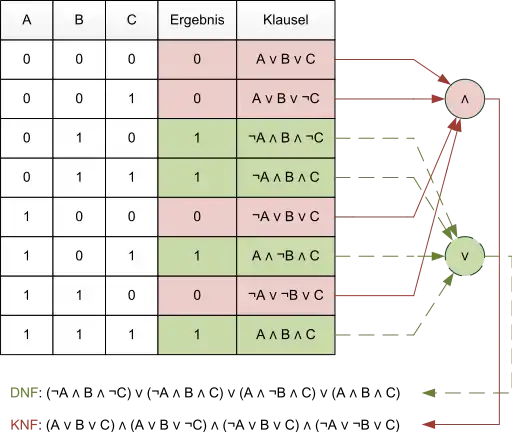
Anmerkung: Die einzelnen Terme sind als Minterme notiert. Außerdem kann man gut sehen, dass jede DNF eine äquivalente KNF besitzt.
Die in DNF dargestellte Funktion
kann auch als vollständig geklammerter Boolescher Ausdruck dargestellt werden:
Üblicherweise werden die inneren -Verknüpfungen analog zu den Multiplikations-Operatoren gesehen und können deshalb weggelassen werden. So ergibt sich eine noch kompaktere Schreibweise, welche man auch Produktterm nennt:
Die Bestimmung des Wahrheitswertes eines Produktterms erfolgt wie in der Mathematik durch Multiplikation der Werte der logischen Variablen. Ist eine der beteiligten Variablen Null, so ist der Wert des gesamten Produktterms Null, der Produktterm nimmt den Wert Eins genau dann an, wenn alle Variablen in ihm den Wert Eins haben.
CPLDs verwenden disjunktiv (ODER) verknüpfte Produktterme, um ihre Funktion zu definieren.
Kanonische disjunktive Normalform
Eine kanonische disjunktive Normalform (KDNF) ist eine DNF, die paarweise voneinander unterschiedliche Minterme enthält, in denen jede Variable genau ein Mal vorkommt.[1] Sie wird auch vollständige disjunktive Normalform genannt. Jede Boolesche Funktion besitzt genau eine KDNF (bis auf Anordnung der Minterme).
In der KDNF sind diejenigen Variablenbelegungen, für die die Funktion den Wert 1 annimmt, durch Minterme ausgedrückt.
Orthogonale disjunktive Normalform
Unter einer orthogonalen disjunktiven Normalform (ODNF) versteht man eine DNF, deren Konjunktionen jeweils paarweise disjunkt sind, d. h. Null ergeben. Um aus einer nichtorthogonalen disjunktiven Normalform eine ODNF zu machen, gibt es verschiedene Orthogonalisierungsverfahren. Man erhält beispielsweise eine ODNF, wenn man aus einem Karnaugh-Veitch-Diagramm nur nichtüberlappende Blöcke ausliest. Im Allgemeinen gibt es zu jeder booleschen Funktion mehrere ODNF. Die kanonische disjunktive Normalform ist „von Hause aus“ orthogonal und eindeutig. ODNF sind aufgrund ihrer Orthogonalität algorithmisch einfacher zu verarbeiten und werden deshalb oft im maschinellen Logikentwurf benutzt. Beispielsweise lässt sich eine ODNF einfach in eine antivalente Normalform umrechnen, indem man alle Disjunktionsoperatoren durch Antivalenzoperatoren ersetzt und anschließend vereinfacht.[2]
Weitere Normalformen
Neben der disjunktiven Normalform gibt es in der Aussagenlogik weitere Normalformen, etwa die konjunktive Normalform und die Negationsnormalform.
Disjunktive Minimalform
Eine disjunktive Normalform heißt disjunktive Minimalform oder minimale disjunktive Normalform[3], wenn
- jede äquivalente Darstellung derselben Ausgabefunktion mindestens genauso viele Produktterme besitzt
- bei jeder äquivalenten Darstellung derselben Ausgabefunktion mit gleich vielen Produkttermen die Anzahl der Eingänge in die Produktterme mindestens genauso groß ist, wie die Anzahl der Eingänge in die Produktterme von f.
Bemerkungen
- In manchen Quellen (zum Beispiel: W. Oberschelp, G. Vossen: Rechneraufbau und Rechnerstrukturen.) versteht man unter DNF genau die kanonische DNF. (Siehe auch: Kanonische Normalform).
- Dieter Bochmann, Bernd Steinbach: Logikentwurf mit XBOOLE: Algorithmen und Programme. Verlag Technik, Berlin 1991, ISBN 3-341-01006-8.
- Manfred Peschel: Moderne Anwendungen algebraischer Methoden. Verlag Technik, Berlin 1971, DNB 575635827.