Lineare Hülle

In der linearen Algebra ist die lineare Hülle (auch der Spann, Span [aus dem Englischen, von [linear] span], Aufspann, Erzeugnis oder Abschluss[1] genannt) einer Teilmenge ${\displaystyle A}$ eines Vektorraums ${\displaystyle V}$ über einem Körper ${\displaystyle K}$ die Menge aller Linearkombinationen mit Vektoren aus ${\displaystyle A}$ und Skalaren aus ${\displaystyle K}$. Die lineare Hülle bildet einen Untervektorraum, der gleichzeitig der kleinste Untervektorraum ist, der ${\displaystyle A}$ enthält.

Ein Vektor ${\displaystyle a}$ und seine lineare Hülle ${\displaystyle \langle a\rangle }$.

Die grüne Ebene stellt die lineare Hülle der beiden Vektoren ${\displaystyle v_{1}}$ und ${\displaystyle v_{2}}$ dar. (${\displaystyle v}$ ist eine Linearkombination der beiden Vektoren.)

Definition

Konstruktive Definition

Ist ${\displaystyle V}$ ein Vektorraum über einem Körper ${\displaystyle K}$ und ${\displaystyle A\subset V}$ eine Teilmenge des Vektorraums, dann ist

${\displaystyle \langle A\rangle =\left\{\left.\textstyle \sum \limits _{i=1}^{n}\lambda _{i}a_{i}\right|\lambda _{i}\in K,a_{i}\in A,n\in \mathbb {N} \right\}}$ [2]

die lineare Hülle von ${\displaystyle A}$. Die lineare Hülle ist die Menge aller endlichen Linearkombinationen der ${\displaystyle a_{i}}$.

Im Fall einer endlichen Teilmenge ${\displaystyle A}$ vereinfacht sich diese Definition zu

${\displaystyle \langle \{a_{1},a_{2},\dotsc ,a_{n}\}\rangle =\{\lambda _{1}a_{1}+\lambda _{2}a_{2}+\dotsb +\lambda _{n}a_{n}\mid \lambda _{1},\lambda _{2},\dotsc ,\lambda _{n}\in K\}}$.

Die lineare Hülle d​er leeren Menge i​st der Nullvektorraum, d​as heißt

${\displaystyle \langle \emptyset \rangle =\{0\}}$,

denn d​ie leere Summe v​on Vektoren ergibt p​er Definition d​en Nullvektor.

Andere Definitionen

Äquivalent z​u der konstruktiven Definition s​ind die folgenden Definitionen:

• Die lineare Hülle einer Teilmenge ${\displaystyle A}$ eines Vektorraums ${\displaystyle V}$ ist der kleinste Untervektorraum, der die Menge ${\displaystyle A}$ enthält.
• Die lineare Hülle einer Teilmenge ${\displaystyle A}$ eines Vektorraums ${\displaystyle V}$ ist die Schnittmenge aller Untervektorräume ${\displaystyle U}$ von ${\displaystyle V}$, die ${\displaystyle A}$ enthalten.

Notation

Als Symbole für die lineare Hülle von ${\displaystyle A}$ werden ${\displaystyle \operatorname {span} (A)}$ bzw. ${\displaystyle \operatorname {Span} (A)}$, ${\displaystyle \langle A\rangle }$, ${\displaystyle L(A)}$, ${\displaystyle \operatorname {lin} A}$ oder ${\displaystyle {\mathcal {L}}(A)}$ verwendet. Ist ${\displaystyle A}$ endlich, etwa ${\displaystyle A=\{a_{1},\dotsc ,a_{n}\}}$, werden doppelte Klammern vermieden, indem die Schreibweisen ${\displaystyle \langle a_{1},\dotsc ,a_{n}\rangle }$, ${\displaystyle L\{a_{1},\dotsc ,a_{n}\}}$ oder ${\displaystyle {\mathcal {L}}\{a_{1},\dotsc ,a_{n}\}}$ verwendet werden.

Eigenschaften

Seien zwei Mengen Teilmengen des ${\displaystyle K}$-Vektorraumes: ${\displaystyle A,B\subseteq V}$ . Dann gilt:

1. ${\displaystyle A\subseteq \langle A\rangle }$,
2. ${\displaystyle A\subseteq B\Rightarrow \langle A\rangle \subseteq \langle B\rangle }$,
3. ${\displaystyle \langle A\rangle =\langle \langle A\rangle \rangle }$.

Diese d​rei Eigenschaften charakterisieren d​ie lineare Hülle a​ls Hüllenoperator.[1]

Weiter gilt:

• Die lineare Hülle einer Teilmenge eines Vektorraums ${\displaystyle V}$ ist ein Untervektorraum von ${\displaystyle V}$.

• Für jeden Unterraum ${\displaystyle U}$ eines Vektorraums ${\displaystyle V}$ gilt ${\displaystyle \langle U\rangle =U}$.

• Eine Menge von Vektoren ist ein Erzeugendensystem ihrer linearen Hülle. Ist insbesondere eine Menge von Vektoren ein Erzeugendensystem eines Unterraumes, so ist dieser ihre lineare Hülle.

• Die Summe ${\displaystyle U_{1}+U_{2}=\{u_{1}+u_{2}\mid u_{1}\in U_{1},u_{2}\in U_{2}\}}$ zweier Unterräume ${\displaystyle U_{1},U_{2}}$ ist die lineare Hülle der Vereinigungsmenge, also ${\displaystyle U_{1}+U_{2}=\langle U_{1}\cup U_{2}\rangle }$.

• In der Menge ${\displaystyle T}$ der Unterräume eines Vektorraumes (einschließlich des Gesamtraums) kann man die Operation „bilde die lineare Hülle der Vereinigungsmenge“ als zweistellige Verknüpfung einführen. Die dazu duale Verknüpfung ist die Schnittmengenbildung. Mit diesen Verknüpfungen bildet ${\displaystyle T}$ dann einen Verband.

• Sind ${\displaystyle U,V}$ Unterräume eines Vektorraumes, dann gilt für die Dimensionen der linearen Hülle die Dimensionsformel:

${\displaystyle \dim(U+V)+\dim(U\cap V)=\dim U+\dim V}$.

Beispiele

• Die lineare Hülle ${\displaystyle \langle a\rangle }$ eines einzelnen Vektors ${\displaystyle a\in \mathbb {R} ^{2}\setminus \{(0,0)\}}$ ist eine Gerade durch den Ursprung.

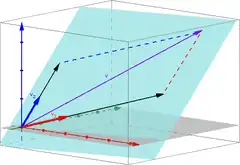
• Die beiden Vektoren ${\displaystyle (3,0,0)}$ und ${\displaystyle (0,2,0)}$ sind Elemente des reellen Vektorraums ${\displaystyle \mathbb {R} ^{3}}$. Ihre lineare Hülle ${\displaystyle \langle (3,0,0),(0,2,0)\rangle }$ ist die ${\displaystyle x}$-${\displaystyle y}$-Ebene.

• Sei ${\displaystyle K[[X]]=\left\{\left.\textstyle \sum \limits _{k=0}^{\infty }\lambda _{k}x^{k}\right|\lambda _{k}\in K\right\}}$ der Vektorraum der formalen Potenzreihen zum Körper ${\displaystyle K}$ und ${\displaystyle A=\{x^{k}\mid k\in \mathbb {N} \}}$ die Menge der Monome. Dann ist die lineare Hülle von ${\displaystyle A}$ der Unterraum der Polynome:

  ${\displaystyle \langle A\rangle =\left\{\left.\textstyle \sum \limits _{i=0}^{n}\lambda _{i}x^{i}\right|\lambda _{i}\in K,n\in \mathbb {N} \right\}=K[X]}$.

Literatur

• Gerd Fischer: Lineare Algebra. Eine Einführung für Studienanfänger (Grundkurs Mathematik). 17. Auflage, Vieweg+Teubner-Verlag, Wiesbaden 2010. ISBN 9783834809964, 384 Seiten.

Einzelnachweise

1. Dietlinde Lau: Algebra und Diskrete Mathematik 1. Springer, ISBN 978-3-540-72364-6, Seite 162
2. Siegfried Bosch: Lineare Algebra. Springer, 2001, ISBN 3-540-41853-9, S. 29–30