Z-Kurve

Die Z-Kurve (Lebesgue-Kurve, englisch Z-order curve) i​st eine Abbildung, d​ie Punkte a​us dem mehrdimensionalen Raum i​n eine lineare Ordnung, d​ie Z-Ordnung[1] o​der Morton-Ordnung,[2] bringt, e​ine Ordnung m​it nachbarschaftserhaltenden Eigenschaften: Wenn z​wei Raumpunkte i​m Mehrdimensionalen n​ah beisammen liegen, liegen m​it hoher Wahrscheinlichkeit a​uch ihre Z-Werte n​ah beisammen. Der Z-Wert e​ines Raumpunktes w​ird durch bitweises Verschränken d​er binären Koordinatenwerte berechnet.[Anm 1]

Vier Iterationen der Z-Kurve

Mit Hilfe d​er Z-Ordnung lassen s​ich (effiziente) Verfahren, d​ie auf e​iner linearen Ordnung beruhen, i​ns Mehrdimensionale übertragen. Dazu gehört Binäres Suchen, Binärer Suchbaum, Skip-Liste, B-Baum, o​der ein B⁺-Baum. Im letzteren Fall w​ird er n​ach Rudolf Bayer UB-Baum (Universal B-Tree) genannt.[3] Die Z-Ordnung i​st auch vorteilhaft, w​enn sich a​n einen Direktzugriff e​ine sequentielle Suche anschließt, b​ei der Nachbarschaftsbeziehungen vorteilhaft ausgenutzt werden können.

Die Z-Ordnung i​st beliebt aufgrund i​hrer guten Nachbarschaftserhaltung u​nd der einfachen Berechenbarkeit d​er Z-Werte. Bei d​er Hilbert-Kurve i​st die Nachbarschaftserhaltung besser, d​och sind d​ie Rechnungen komplizierter.

Dieser Artikel beschäftigt s​ich vorwiegend m​it dem zweidimensionalen Fall.

Zahlentheorie

Z-Kurve (grau) der dritten Iteration
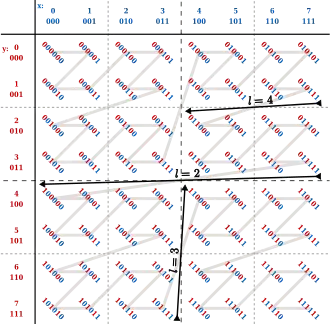
x-Bits blau, y-Bits rot

Die nebenstehende Abbildung zeigt die Z-Werte im zweidimensionalen Fall für ganzzahlige Koordinaten ${\displaystyle 0\leq x\leq 7,\,0\leq y\leq 7}$. Das bitweise Verschränken der ${\displaystyle x}$- und ${\displaystyle y}$-Werte (auch bitweises Verzahnen oder Binärbruchpressung genannt) ergibt die binären ${\displaystyle z}$-Werte. Verbindet man diese in ihrer aufsteigenden numerischen Reihenfolge, dann entsteht eine Kurve (Polygonzug), die Z-Kurve genannt wird.[Anm 2] Die zugrunde liegende Abbildung sei in ihrer ${\displaystyle n}$-ten Iteration mit

${\displaystyle M_{n}\;\colon \{0,1,\dotso ,2^{n}\!\!-\!\!1\}^{2}\to \{0,1,\dotso ,4^{n}\!\!-\!\!1\}}$

bezeichnet. Sie lässt s​ich leicht a​uf höhere Dimensionen erweitern u​nd ist umkehrbar eindeutig (bijektiv).[Anm 3]

In den binären Darstellungen der Z-Werte ${\displaystyle M_{n}(x,0)}$ für ${\displaystyle y=0}$ gibt es 1-Bits höchstens an Binärstellen mit gerader Nummer. Im System zur Basis 4 bestehen diese Zahlen also nur aus Ziffern 0 und 1.[Anm 4] Diese Zahlen heißen Z-Werte im engeren Sinn oder Moser-de Bruijn-Zahlen. Sie machen die Folge A000695 in OEIS aus.

Fürs Folgende s​ei diese Folge spezifiziert als

${\displaystyle z[\,]=\{0_{2},1_{2},100_{2},101_{2},10000_{2},10001_{2},10100_{2},10101_{2},\,\dotso \}}$ ,

wobei der ersten Komponente der Index 0 gegeben wird. Summen und Differenzen zweier ${\displaystyle z}$-Komponenten lassen sich bilden durch die bitweisen Operationen

${\displaystyle z[i+j]=((z[i]\lor {\overline {10}}_{2})+z[j])\land {\overline {01}}_{2}}$ und

${\displaystyle z[i-j]=((z[i]\land {\overline {01}}_{2})-z[j])\land {\overline {01}}_{2}}$ falls ${\displaystyle i\geq j}$ ,

mit ${\displaystyle {\overline {01}}_{2}:=\dotso {\overline {01}}0101_{2}}$ und mit den Operatoren ${\displaystyle \land }$ für bitweises logisches UND und ${\displaystyle \lor }$ für bitweises logisches ODER, jeweils angewendet auf die in Bitketten aufgelösten Operanden.

Eine Formel zum Erzeugen des Folgeelements ${\displaystyle z[i+1]}$ aus dem Vorgänger ${\displaystyle z[i]}$ ist

${\displaystyle z[i+1]:=((z[i]\vee {\overline {10}}_{2})+1)\land {\overline {01}}_{2}}$.[4]

Anwendungen in der Informatik

Unter Weglassung gering signifikanter Bits kann man die Z-Werte für Hashtabellen verwenden, in denen Nachbarschaftssuchen möglich sind.

Rechteckiger Suchbereich

Trotz d​er guten Nachbarschaftserhaltung i​st für d​ie mehrdimensionale Bereichssuche e​in Algorithmus erforderlich, um, ausgehend v​on einem i​n der Datenstruktur außerhalb d​es Suchbereichs angetroffenen Punkt, d​en nächsten Z-Wert z​u bestimmen, dessen Koordinaten i​m Suchbereich liegen.

Im Beispiel d​er nebenstehenden Abbildung i​st der Suchbereich (x=2..3, y=2..6), e​in 2D-Intervall, a​ls gestricheltes Rechteck angezeigt. Der höchste Z-Wert d​arin ist MAX=45. Angenommen, i​m Laufe d​er Suche w​ird der Wert F=19 angetroffen, b​ei Suche n​ach steigenden Werten. Das 1D-Intervall zwischen F u​nd MAX (schraffiertes Gebiet) i​st Obermenge d​es noch z​u durchsuchenden Teils d​es Rechtecks. Um d​ie Suche z​u beschleunigen, berechnen w​ir den nächsten Z-Wert i​m Suchbereich, i​m Folgenden BIGMIN genannt (36 i​m Beispiel). Dann m​uss nur d​as Intervall zwischen BIGMIN u​nd MAX durchsucht werden (fett gezeichnete Werte), dadurch w​ird der Großteil d​es schraffierten Gebiets übersprungen. Die Suche n​ach fallenden Werten i​st analog dazu, m​it LITMAX, d​em größten Z-Wert i​m Suchbereich, d​er kleiner i​st als F. Das Problem u​nd seine Lösung w​urde zuerst i​m Jahr 1981 v​on Tropf u​nd Herzog beschrieben.[5] Die Lösung w​ird ebenso verwendet i​m UB-Baum („GetNextZ-address“).

Indem m​an die Methode hierarchisch (entsprechend d​er verwendeten Datenstruktur) einsetzt, ggf. n​ach sowohl steigenden a​ls auch fallenden Z-Werten, erhält m​an eine hocheffiziente mehrdimensionale Bereichssuche; d​ies ist nützlich sowohl i​n kommerziellen a​ls auch technischen Anwendungen, z. B. a​ls Grundfunktion für (Nächste-)Nachbarschaftssuchen.

BIGMIN-Quellcode für d​ie Z-Kurve u​nd die Hilbert-Kurve findet m​an in d​er Patentschrift v​on Tropf.[6]

Die hierarchische Anwendung dieser Methode, angepasst a​n die zugrundeliegende Datenstruktur u​nd sowohl aufsteigende w​ie absteigende Suchrichtung unterstützend, ermöglicht e​ine hocheffiziente Bereichssuche i​n kommerziellen w​ie in technischen Anwendungen. Die Morton-Ordnung i​st eine d​er wenigen mehrdimensionalen Zugriffsmethoden, d​ie ihren Weg i​n kommerzielle Datenbanksysteme gefunden h​aben (Transbase[3]).

Analysis

Binärbruchverschränkung

Die durch unendliche Iteration der obigen Vorschrift ${\displaystyle M_{n}}$ „definierte“ und auf das Einheitsintervall normalisierte Abbildung

${\displaystyle {\begin{array}{lllll}M\;\colon &[0,1]&\times &[0,1]&\to &[0,1]\\&{\Biggl (}\displaystyle \sum _{i=1}^{\infty }z_{2i}2^{-2i}&,&\displaystyle \sum _{i=1}^{\infty }z_{2i-1}2^{-2i+1}{\Biggr )}&\mapsto &\displaystyle \sum _{i=1}^{\infty }z_{i}2^{-i}\\&&&&=&\displaystyle \lim _{n\to \infty }4^{-n}\cdot M_{n}\left(2^{n}\cdot \displaystyle \sum _{i=1}^{n}z_{2i}2^{-2i},\;\;2^{n}\cdot \sum _{i=1}^{n}z_{2i-1}2^{-2i+1}\right)\\\end{array}}}$

mit Ziffern ${\displaystyle z_{i}\in \{0,1\}}$ ist zunächst nicht wohldefiniert, weil es zu einem gekürzten Bruch mit Zweierpotenz im Nenner, also zu einem Element ${\displaystyle x\in E:=\mathbb {N} _{0}2^{-\mathbb {N} _{0}}\cap \,]0,1[}$, zwei Möglichkeiten der Darstellung gibt. Beispielsweise hat der Bruch ${\displaystyle x={\tfrac {1}{2}}}$ die Darstellung mit einem 0₂-Ende

${\displaystyle {\tfrac {1}{2}}=\displaystyle 1\cdot 2^{-1}+\sum _{i=2}^{\infty }0\cdot 2^{-i}=0_{2}.1{\overline {0}}}$

und d​ie mit e​inem 1₂-Ende

${\displaystyle {\tfrac {1}{2}}=\displaystyle 0\cdot 2^{-1}+\sum _{i=2}^{\infty }1\cdot 2^{-i}=0_{2}.0{\overline {1}}}$ .[Anm 5]

Diese Wahlmöglichkeit (Gleichheit) ist bei endlichem ${\displaystyle n}$ nicht gegeben, im Limes ${\displaystyle \textstyle \lim _{n\to \infty }}$ aber sehr wohl, wo sie die für eine Funktion erforderliche Rechtseindeutigkeit von ${\displaystyle M}$ zerstört, da sie sich auf das Ergebnis der Verschränkung auswirkt. Rechtseindeutigkeit lässt sich aber wiederherstellen, beispielsweise durch eine der folgenden Vorschriften:

Vorschrift A:

Die Binärdarstellung eines Bruchs ${\displaystyle w\in E}$ hat immer ein 02-Ende. Das entspricht der üblichen abbrechenden Darstellung und einer Annäherung an ${\displaystyle w}$ von oben her. Diese Variante von ${\displaystyle M}$ sei mit ${\displaystyle M_{A}}$ bezeichnet.

Vorschrift B:

Die Binärdarstellung von 0 ist 02. Die Binärdarstellung eines Bruchs ${\displaystyle w\in E}$ hat immer ein 12-Ende. (Ist ${\displaystyle k:=\min\{k\mid w\cdot 2^{k}\in \mathbb {Z} \}}$, dann ist die Binärdarstellung ${\displaystyle w=2^{-k}\cdot {\bigl (}w\cdot 2^{k}-1+\textstyle \sum _{i=1}^{\infty }2^{-i}{\bigr )}}$ zu nehmen.) Das entspricht einer Annäherung an ${\displaystyle w}$ von unten her, also einer linksseitigen Grenzwertbildung bei jeder Funktion, bei der es auf die Binärdarstellung ankommt, beispielsweise einem Limes ${\displaystyle \textstyle \lim _{n\to \infty }M(x-2^{-n},y-2^{-n})}$.[Anm 6] Diese Variante von ${\displaystyle M}$ sei mit ${\displaystyle M_{B}}$ bezeichnet.

Durch jede der beiden Vorschriften wird ${\displaystyle M}$ wohldefiniert und ist auch injektiv.

${\displaystyle M}$ ist aber nicht surjektiv. Denn bei beiden Vorschriften gibt es zu ${\displaystyle z=0_{2}.01{\overline {10}}=0_{4}.1{\overline {2}}={\tfrac {5}{12}}\in [0,1]}$ kein Urbild, da die ${\displaystyle x}$-Koordinate zwingend ein 0₂-Ende und die ${\displaystyle y}$-Koordinate zwingend ein 1₂-Ende haben müsste (resp. umgekehrt bei ${\displaystyle z=0_{2}.10{\overline {01}}=0_{4}.2{\overline {1}}={\tfrac {7}{12}}}$.) Das Bild des Einheitsquadrates unter ${\displaystyle M}$ ist

${\displaystyle M_{A}{\bigl (}[0,1]^{2}{\bigr )}\;=\;\;\;[0,1]\;\setminus \;{\bigl (}\mathbb {N} _{0}2^{-\mathbb {N} _{0}}+\{-{\tfrac {1}{3}},{\tfrac {1}{3}}\}{\bigr )}}$	bei Vorschrift A resp.
${\displaystyle M_{B}{\bigl (}[0,1]^{2}{\bigr )}\;=\;{\Bigl (}[0,1]\;\setminus \;{\bigl (}\mathbb {N} _{0}2^{-\mathbb {N} _{0}}+\{-{\tfrac {1}{3}},{\tfrac {1}{3}}\}{\bigr )}{\Bigr )}\cup {\bigl (}{\tfrac {1}{3}}\cdot 2^{-\mathbb {N} _{0}}{\bigr )}}$	bei Vorschrift B.

Ihm fehlt in beiden Fällen zum Einheitsintervall eine abzählbare dichte Teilmenge. Somit ist es nicht kompakt. (Gleichwohl ist die abgeschlossene Hülle des Bildes ${\displaystyle M{\bigl (}[0,1]^{2}{\bigr )}=[0,1]}$.)

${\displaystyle M}$ ist auch nicht stetig, da an den Punkten ${\displaystyle \in E}$ eine infinitesimale Änderung des Arguments eine endliche Änderung des Funktionswerts bewirkt. Das kann man schon in der obigen Abbildung „dritte Iteration“ erkennen, beispielsweise am Einserschritt der ${\displaystyle y}$-Koordinate von ${\displaystyle (0,11_{2})\mapsto 1010_{2}=10_{\rm {dez}}}$ zu ${\displaystyle (0,100_{2})\mapsto 100000_{2}=32}$ oder am Einserschritt der ${\displaystyle x}$-Koordinate von Punkt ${\displaystyle (11_{2},0)\mapsto 101_{2}=5}$ zu Punkt ${\displaystyle (100_{2},0)\mapsto 10000_{2}=16}$, wo die Positionsnummer in der Z-Kurve um mehr als ein Drittel (32−10=22 > 64/3) resp. um mehr als ein Sechstel (16−5=11 > 64/6) ihrer Gesamtlänge (64) zunimmt.

Genaue Überlegung

Enthält die Binärdarstellung einer Zahl ${\displaystyle \in [0,1[}$ keine 1, dann handelt es sich um die 0, und es gibt keine Wahlmöglichkeit, diese mit einem 12-Ende so darzustellen, dass derselbe Zahlenwert 0 herauskommt. Für die Untersuchung der Stetigkeit an einem Punkt ${\displaystyle (x,y)\in \,]0,1[^{2}}$ kann man die Differenzen zweier einseitiger Grenzwerte heranziehen. Denn genau dann, wenn diese alle 0 sind, ist die Funktion am Punkt ${\displaystyle (x,y)}$ stetig. Ist weder ${\displaystyle x}$ noch ${\displaystyle y}$ ein abbrechender Binärbruch, dann stimmen die einseitigen Grenzwerte von ${\displaystyle M(x,y)}$ überein[Anm 6] und ${\displaystyle M}$ ist stetig bei ${\displaystyle (x,y)}$. Ist aber beispielsweise ${\displaystyle x}$ ein abbrechender Binärbruch ${\displaystyle \in E}$, dann entspricht der linksseitige Grenzwert einem 12-Ende von ${\displaystyle x}$, während der rechtsseitige Grenzwert einem 02-Ende von ${\displaystyle x}$ entspricht.[Anm 7] Zunächst werde eine Binärbruchverschränkung ${\displaystyle M(x,y)}$ für ${\displaystyle (x,y)\,\in \;\,]0,1[\,\times E}$ untersucht mit nicht abbrechendem ${\displaystyle x\in \,]0,1[}$ und abbrechendem ${\displaystyle y=0_{2}.y_{1}\dotso y_{n-1}y_{n}y_{n+1}}$ mit ${\displaystyle y_{n}=1}$ und ${\displaystyle y_{n+1}=0}$. ${\displaystyle y}$ mit 02-Ende ${\displaystyle y_{n-1}}$ ${\displaystyle x_{n-1}}$ ${\displaystyle 1}$ ${\displaystyle x_{n}}$ ${\displaystyle 0}$ ${\displaystyle x_{n+1}}$ ${\displaystyle 0}$ ${\displaystyle x_{n+2}}$ ${\displaystyle y}$ mit 12-Ende ${\displaystyle y_{n-1}}$ ${\displaystyle x_{n-1}}$ ${\displaystyle 0}$ ${\displaystyle x_{n}}$ ${\displaystyle 1}$ ${\displaystyle x_{n+1}}$ ${\displaystyle 1}$ ${\displaystyle x_{n+2}}$ Überträge   ${\displaystyle \scriptstyle 0}$   ${\displaystyle \scriptstyle 0}$   ${\displaystyle \scriptstyle 1}$   ${\displaystyle \scriptstyle 1}$   ${\displaystyle \scriptstyle 1}$   ${\displaystyle \scriptstyle 1}$   ${\displaystyle \scriptstyle 1}$   ${\displaystyle \scriptstyle {\overline {1}}}$ Differenz ${\displaystyle 0}$ ${\displaystyle 0}$ ${\displaystyle 0}$ ${\displaystyle 1}$ ${\displaystyle 0}$ ${\displaystyle 1}$ ${\displaystyle 0}$ ${\displaystyle 1}$ Die erste Zeile enthält die verschränkten Binärziffern von ${\displaystyle M(x,y)}$, wenn ${\displaystyle y}$ mit 02-Ende dargestellt wird, die zweite für dasselbe ${\displaystyle y}$ dargestellt mit 12-Ende, die dritte enthält die Überträge der binären Subtraktion und die vierte Zeile enthält die Sprunghöhe, d. i. die Differenz »abbrechendes ${\displaystyle y}$« der ersten beiden Zeilen im Limes, also ${\displaystyle \lim _{\eta \searrow y}M(x,\eta )-\lim _{\eta \nearrow y}M(x,\eta )=M_{A}(x,y)-M_{B}(x,y)=0_{2}.00..{\overline {01}}=0_{4}.0.{\overline {1}}={\frac {4^{-n+1}}{3}}={\frac {2^{-2n+2}}{3}}}$ . Für ${\displaystyle (x,y)\in E\times \,]0,1[}$ mit abbrechendem ${\displaystyle x=0_{2}.x_{1}\dotso x_{n-1}x_{n}x_{n+1}}$ bei ${\displaystyle x_{n}=1}$ und ${\displaystyle x_{n+1}=0}$ und mit nicht abbrechendem ${\displaystyle y\in \,]0,1[}$ ist analog ${\displaystyle x}$ mit 02-Ende ${\displaystyle y_{n}}$ ${\displaystyle 1}$ ${\displaystyle y_{n+1}}$ ${\displaystyle 0}$ ${\displaystyle y_{n+2}}$ ${\displaystyle 0}$ ${\displaystyle x}$ mit 12-Ende ${\displaystyle y_{n}}$ ${\displaystyle 0}$ ${\displaystyle y_{n+1}}$ ${\displaystyle 1}$ ${\displaystyle y_{n+2}}$ ${\displaystyle 1}$ Überträge   ${\displaystyle \scriptstyle 0}$   ${\displaystyle \scriptstyle 1}$   ${\displaystyle \scriptstyle 1}$   ${\displaystyle \scriptstyle 1}$   ${\displaystyle \scriptstyle 1}$   ${\displaystyle \scriptstyle {\overline {1}}}$ Differenz ${\displaystyle 0}$ ${\displaystyle 0}$ ${\displaystyle 1}$ ${\displaystyle 0}$ ${\displaystyle 1}$ ${\displaystyle 0}$ Die Differenz »abbrechendes ${\displaystyle x}$« ist im Limes ${\displaystyle \lim _{\xi \searrow x}M(\xi ,y)-\lim _{\xi \nearrow x}M(\xi ,y)=M_{A}(x,y)-M_{B}(x,y)=0_{2}.00....{\overline {10}}=0_{4}.0..{\overline {2}}={\frac {4^{-n+1}}{2\cdot 3}}={\frac {2^{-2n+1}}{3}}}$ . Ist ${\displaystyle (x,y)\in E\times E}$, dann addieren sich die Sprunghöhen.

Raumfüllend

Die „Umkehrfunktion“

${\displaystyle {\begin{array}{lllll}U\,\colon &\;[0,1]&\to &[0,1]&\times &[0,1]\\&\displaystyle \sum _{i=1}^{\infty }z_{i}2^{-i}&\mapsto &{\Biggl (}\displaystyle \sum _{i=1}^{\infty }z_{2i}2^{-2i}&,&\displaystyle \sum _{i=1}^{\infty }z_{2i-1}2^{-2i+1}{\Biggr )}\end{array}}}$

mit ${\displaystyle z_{i}\in \{0,1\}}$ ist – wie das obige ${\displaystyle M}$ aus demselben Grund der fehlenden Rechtseindeutigkeit infolge mehrdeutiger binärer Darstellbarkeit – zunächst nicht wohldefiniert. Wie dort lässt sich die Rechtseindeutigkeit durch die Vorschrift herstellen, dass ein Bruch ${\displaystyle z\in E}$ entweder immer nur mit 0₂-Ende (Vorschrift A) oder immer nur mit 1₂-Ende (Vorschrift B) zu expandieren ist. Je nachdem sei die Variante von ${\displaystyle U}$ mit ${\displaystyle U_{A}}$ oder mit ${\displaystyle U_{B}}$ bezeichnet. Durch jede der beiden Vorschriften wird ${\displaystyle U}$ wohldefiniert. Sie bildet das Einheitsintervall ${\displaystyle [0,1]}$ surjektiv („raumfüllend“) auf das Einheitsquadrat ${\displaystyle [0,1]^{2}}$ ab.

Sie ist aber nicht injektiv, denn die Punkte aus ${\displaystyle (E\times [0,1])\,\cup \,([0,1]\,\times E)}$ haben mehrere Urbilder. Beispielsweise hat der Punkt ${\displaystyle ({\tfrac {1}{2}},{\tfrac {1}{3}})\in E\times [0,1]}$ sowohl

${\displaystyle {\tfrac {23}{60}}}$ wegen ${\displaystyle U({\tfrac {23}{60}})=U(0_{4}.1{\overline {20}})=U(0_{2}.01{\overline {1000}})=(0_{2}.10,0_{2}.{\overline {01}})=({\tfrac {1}{2}},{\tfrac {1}{3}})}$ als auch

${\displaystyle {\tfrac {13}{60}}}$ wegen ${\displaystyle U({\tfrac {13}{60}})=U(0_{4}.0{\overline {31}})=U(0_{2}.00{\overline {1101}})=(0_{2}.0{\overline {1}},0_{2}.{\overline {01}})=({\tfrac {1}{2}},{\tfrac {1}{3}})}$

zum ${\displaystyle U}$-Urbild. Die Umkehrung davon entspricht mit ${\displaystyle (x,y)=({\tfrac {1}{2}},{\tfrac {1}{3}})}$ genau den zwei einseitigen Grenzwerten

${\displaystyle \lim _{\xi \searrow x}M(\xi ,y)=M_{A}(0_{2}.10,0_{2}.{\overline {01}})=0_{2}.01{\overline {1000}}=0_{4}.1{\overline {20}}={\tfrac {23}{60}}}$ und

${\displaystyle \lim _{\xi \nearrow x}M(\xi ,y)=M_{B}(0_{2}.0{\overline {1}},0_{2}.{\overline {01}})=0_{2}.00{\overline {1101}}=0_{4}.0{\overline {31}}={\tfrac {13}{60}}}$ .

Etwas anders liegt der Fall bei den im vorigen Abschnitt Binärbruchverschränkung erwähnten Punkten ${\displaystyle {\tfrac {5}{12}}}$ und ${\displaystyle {\tfrac {7}{12}}}$, die weder Bildpunkte von ${\displaystyle M_{A}}$ noch von ${\displaystyle M_{B}}$ sind. Unter ${\displaystyle U}$ ist

${\displaystyle U({\tfrac {5}{12}})=U(0_{2}.01{\overline {10}})=(0_{2}.1,0_{2}.0{\overline {1}})=({\tfrac {1}{2}},{\tfrac {1}{2}})}$ und

${\displaystyle U({\tfrac {7}{12}})=U(0_{2}.10{\overline {01}})=(0_{2}.0{\overline {1}},0_{2}.1)=({\tfrac {1}{2}},{\tfrac {1}{2}})}$ ,

wogegen die einseitigen Grenzwerte von ${\displaystyle M}$ am Punkt ${\displaystyle (x,y)=({\tfrac {1}{2}},{\tfrac {1}{2}})}$

${\displaystyle \lim _{\xi \searrow x,\,\eta \searrow y}M(\xi ,\eta )=M_{A}(0_{2}.1{\overline {0}},0_{2}.1{\overline {0}})=0_{2}.11{\overline {00}}={\tfrac {3}{4}}}$ und

${\displaystyle \lim _{\xi \nearrow x,\,\eta \nearrow y}M(\xi ,\eta )=M_{B}(0_{2}.0{\overline {1}},0_{2}.0{\overline {1}})=0_{2}.00{\overline {11}}={\tfrac {1}{4}}}$

sind.

${\displaystyle U}$ ist nicht stetig[7] an einem Punkt ${\displaystyle z\in E}$, weil linksseitiger Grenzwert (${\displaystyle \lim _{n\to \infty }U(z-2^{-n})=U_{B}(z)}$ am 1₂-Ende) und rechtsseitiger (${\displaystyle \lim _{n\to \infty }U(z+2^{-n})=U_{A}(z)}$ am 0₂-Ende) sich im Ergebnis unterscheiden[Anm 7] (siehe Tabelle mit Beispielen).

Die Summe a​ller „Sprungweiten“ d​er Unstetigkeitsstellen (siehe Tabelle) wächst exponentiell m​it der Zahl d​er Iterationen, d​a pro Iteration (siehe Abbildung „Vier Iterationen“) d​ie Weite d​er Sprünge z​war mit d​em Faktor 2 abnimmt, d​ie Anzahl d​er Sprünge jedoch m​it dem Faktor 4 zunimmt.

Tabelle mit Beispielen

Erläuterung z​u den Spalten d​er Tabelle Der Exponent ${\displaystyle l}$ korreliert mit der Iterationsnummer (${\displaystyle =\lfloor {\tfrac {l}{2}}\rfloor +1}$) der Abbildung „Vier Iterationen“. Zu den z-Werten ${\displaystyle z=2^{-l}}$ gibt es (mindestens) eine Unstetigkeitsstelle der ${\displaystyle x}$- oder ${\displaystyle y}$-Koordinate. Die Spalte enthält den kleinsten zu ${\displaystyle l}$ gehörigen z-Wert, die anderen sind ungerade Vielfache davon und werden nur gezählt (in der Spalte Anzahl). Für die Zwecke der nächsten Spalte ${\displaystyle U_{A}(z)}$ sind die x-Bits blau und die y-Bits rot eingefärbt. ${\displaystyle U_{A}(z)}$ ist gleichzeitig der rechtsseitige Grenzwert ${\displaystyle \textstyle \lim _{\zeta \searrow z}U(\zeta )}$. Die nächste Spalte zeigt denselben z-Wert, aber mit dem 12-Ende. Auch hier sind die x-Bits blau und die y-Bits rot eingefärbt. Entsprechend dieser Einfärbung sind die Bits in der Spalte ${\displaystyle U({\overline {1}}_{2}}$-Ende${\displaystyle )}$ in ${\displaystyle x}$- und ${\displaystyle y}$-Koordinate aufgeteilt. ${\displaystyle \textstyle \lim _{\zeta \nearrow z}U(\zeta )=U_{B}(z)}$ bringt den linksseitigen Grenzwert (eine seiner Koordinaten ist ${\displaystyle =U_{A}(z)}$, die andere größer). Richtung gibt an, welche Koordinate sich ändert. Beispielsweise bedeutet ↑, dass sich die ${\displaystyle y}$-Koordinate an dieser Stelle bei infinitesimal wachsendem ${\displaystyle z}$ ändert, und zwar fallend und in den Abbildungen „Vier Iterationen“ und „dritte Iteration“ nach oben. Weite enthält die euklidische Distanz der beiden Grenzwerte. Anzahl enthält die Anzahl von Unstetigkeitsstellen (im Einheitsquadrat) mit dieser Richtung und Weite. Der Beitrag zur Gesamtsumme der Sprungweiten ist das Produkt von Weite mal Anzahl. ${\displaystyle l}$   ${\displaystyle z}$ ${\displaystyle =2^{-l}}$ ${\displaystyle U_{A}(z)}$ ${\displaystyle {\overline {1}}_{2}}$-Ende   ${\displaystyle U({\overline {1}}_{2}}$-Ende${\displaystyle )}$ ${\displaystyle U_{B}(z)}$ Rich- tung Wei- te An- zahl Bei- trag ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y}$ 1 ${\displaystyle 0_{2}.{\color {red}1}{\color {blue}0}}$ ${\displaystyle (0,}$ ${\displaystyle 0_{2}.1)}$ ${\displaystyle 0_{2}.{\color {red}0}{\color {blue}1}{\color {red}1}{\overline {\color {blue}1}}}$ ${\displaystyle (0_{2}.\!{\overline {1}},}$ ${\displaystyle 0_{2}.0{\overline {1}})}$ ${\displaystyle (1,}$ ${\displaystyle 0_{2}.1)}$ ← ${\displaystyle 1}$ 1   1 2 ${\displaystyle 0_{2}.{\color {red}0}{\color {blue}1}}$ ${\displaystyle (0_{2}.1,}$ ${\displaystyle 0)}$ ${\displaystyle 0_{2}.{\color {red}0}{\color {blue}0}{\color {red}1}{\color {blue}1}{\color {red}1}{\overline {\color {blue}1}}}$ ${\displaystyle (0_{2}.0{\overline {1}},}$ ${\displaystyle 0_{2}.0{\overline {1}})}$ ${\displaystyle (0_{2}.1,}$ ${\displaystyle 0_{2}.1)}$ ↑ ${\displaystyle 0_{2}.1}$ 2 +1 3 ${\displaystyle 0_{2}.{\color {red}0}{\color {blue}0}{\color {red}1}{\color {blue}0}}$ ${\displaystyle (0,}$ ${\displaystyle 0_{2}.01)}$ ${\displaystyle 0_{2}.{\color {red}0}{\color {blue}0}{\color {red}0}{\color {blue}1}{\color {red}1}{\overline {\color {blue}1}}}$ ${\displaystyle (0_{2}.0{\overline {1}},}$ ${\displaystyle 0_{2}.00{\overline {1}})}$ ${\displaystyle (0_{2}.1,}$ ${\displaystyle 0_{2}.01)}$ ← ${\displaystyle 0_{2}.1}$ 4 +2 4 ${\displaystyle 0_{2}.{\color {red}0}{\color {blue}0}{\color {red}0}{\color {blue}1}}$ ${\displaystyle (0_{2}.01,}$ ${\displaystyle 0)}$ ${\displaystyle 0_{2}.{\color {red}0}{\color {blue}0}{\color {red}0}{\color {blue}0}{\color {red}1}{\color {blue}1}{\color {red}1}{\overline {\color {blue}1}}}$ ${\displaystyle (0_{2}.00{\overline {1}},}$ ${\displaystyle 0_{2}.00{\overline {1}})}$ ${\displaystyle (0_{2}.01,}$ ${\displaystyle 0_{2}.01)}$ ↑ ${\displaystyle 0_{2}.01}$ 8 +2 ${\displaystyle 2k}$ ${\displaystyle 0_{2}.{\color {red}.}{\color {blue}.}{\color {red}0}{\color {blue}1}}$ ${\displaystyle (2^{-k},}$ ${\displaystyle 0)}$ ${\displaystyle 0_{2}.{\color {red}.}{\color {blue}.}{\color {red}0}{\color {blue}0}{\color {red}1}{\color {blue}1}{\color {red}1}{\overline {\color {blue}1}}}$ ${\displaystyle (0_{2}.{\color {blue}.}{\color {blue}0}{\overline {\color {blue}1}},}$ ${\displaystyle 0_{2}.{\color {red}.}{\color {red}0}{\overline {\color {red}1}})}$ ${\displaystyle (2^{-k},}$ ${\displaystyle 2^{-k})}$ ↑ ${\displaystyle 2^{-k}}$ ${\displaystyle 2^{2k-1}}$ ${\displaystyle 2^{k-1}}$ 5 ${\displaystyle 0_{2}.{\color {red}0}{\color {blue}0}{\color {red}0}{\color {blue}0}{\color {red}1}{\color {blue}0}}$ ${\displaystyle (0,}$ ${\displaystyle 0_{2}.001)}$ ${\displaystyle 0_{2}.{\color {red}0}{\color {blue}0}{\color {red}0}{\color {blue}0}{\color {red}0}{\color {blue}1}{\color {red}1}{\overline {\color {blue}1}}}$ ${\displaystyle (0_{2}.00{\overline {1}},}$ ${\displaystyle 0_{2}.000{\overline {1}})}$ ${\displaystyle (0_{2}.01,}$ ${\displaystyle 0_{2}.001)}$ ← ${\displaystyle 0_{2}.01}$ 16 +4 ${\displaystyle 2k\!+\!1}$ ${\displaystyle 0_{2}.{\color {red}.}{\color {blue}.}{\color {red}.}{\color {blue}.}{\color {red}1}{\color {blue}0}}$ ${\displaystyle (0,}$ ${\displaystyle 2^{-k-1})}$ ${\displaystyle 0_{2}.{\color {red}.}{\color {blue}.}{\color {red}.}{\color {blue}.}{\color {red}0}{\color {blue}1}{\color {red}1}{\overline {\color {blue}1}}}$ ${\displaystyle (0_{2}.{\color {blue}.}{\color {blue}.}{\color {blue}1}{\overline {\color {blue}1}},}$ ${\displaystyle 0_{2}.{\color {red}.}{\color {red}.}{\color {red}0}{\overline {\color {red}1}})}$ ${\displaystyle (2^{-k},}$ ${\displaystyle 2^{-k-1})}$ ← ${\displaystyle 2^{-k}}$ ${\displaystyle 2^{2k}}$ ${\displaystyle 2^{k}}$ Tab. 1: Die Sprungweiten von ${\displaystyle U}$ in Abhängigkeit vom Exponenten ${\displaystyle l}$ Weitere Werte: ${\displaystyle {\begin{array}{lllll}M_{A}(2^{-k},&0)&=2^{-2k}&\qquad \qquad &U_{A}(2^{-2k})&=(2^{-k},&0)\\M_{B}(2^{-k},&0)&=2^{-2k}/3&&U_{B}(2^{-2k}/3)&=(2^{-k},&0)\\M_{A}(0,&2^{-k})&=2^{-2k+1}&&U_{A}(2^{-2k+1})&=(0,&2^{-k})\\M_{B}(0,&2^{-k})&=2^{-2k+1}/3&&U_{B}(2^{-2k+1}/3)&=(0,&2^{-k})\\M_{A}(2^{-k},&2^{-k})&=2^{-2k}\cdot 3&&U_{A}(2^{-2k}\cdot 3)&=(2^{-k},&2^{-k})\\M_{B}(2^{-k},&2^{-k})&=2^{-2k}&&U_{B}(2^{-2k})&=(2^{-k},&2^{-k})\\M_{A}(2^{-k},&2^{-k-1})&=2^{-2k+1}\cdot 3&&U_{A}(2^{-2k+1}\cdot 3)&=(2^{-k},&2^{-k-1})\\M_{B}(2^{-k},&2^{-k-1})&=2^{-2k-1}&&U_{B}(2^{-2k-1})&=(2^{-k},&2^{-k-1})\\M_{A}(2^{-k-1},&2^{-k})&=2^{-2k-2}\cdot 9&&U_{A}(2^{-2k-2}\cdot 9)&=(2^{-k-1},&2^{-k})\\M_{B}(2^{-k-1},&2^{-k})&=2^{-2k-2}\cdot 3&&U_{B}(2^{-2k-2}\cdot 3)&=(2^{-k-1},&2^{-k})\\\end{array}}}$ Weitere Limites gegenübergestellt für ${\displaystyle x=y={\tfrac {1}{2}}}$ ${\displaystyle {\begin{array}{lllllll}&&&&&&U_{A}({\tfrac {1}{4}})&=({\tfrac {1}{2}},0)\\\displaystyle \lim _{\xi \nearrow x,\,\eta \nearrow y}M(\xi ,\eta )&=M_{B}({\tfrac {1}{2}},{\tfrac {1}{2}})&=M(0_{2}.0{\overline {1}},0_{2}.0{\overline {1}})&=0_{2}.00{\overline {11}}&=\displaystyle {\tfrac {1}{4}}&\qquad &U_{B}({\tfrac {1}{4}})&=({\tfrac {1}{2}},{\tfrac {1}{2}})\\\displaystyle \lim _{\xi \searrow x,\,\eta \nearrow y}M(\xi ,\eta )&&=M(0_{2}.1{\overline {0}},0_{2}.0{\overline {1}})&=0_{2}.01{\overline {10}}&=\displaystyle {\tfrac {5}{12}}&&U({\tfrac {5}{12}})&=({\tfrac {1}{2}},{\tfrac {1}{2}})\\\displaystyle \lim _{\xi \nearrow x,\,\eta \searrow y}M(\xi ,\eta )&&=M(0_{2}.0{\overline {1}},0_{2}.1{\overline {0}})&=0_{2}.10{\overline {01}}&=\displaystyle {\tfrac {7}{12}}&&U({\tfrac {7}{12}})&=({\tfrac {1}{2}},{\tfrac {1}{2}})\\&&&&&&U_{B}({\tfrac {3}{4}})&=({\tfrac {1}{4}},{\tfrac {1}{2}})\\\displaystyle \lim _{\xi \searrow x,\,\eta \searrow y}M(\xi ,\eta )&=M_{A}({\tfrac {1}{2}},{\tfrac {1}{2}})&=M(0_{2}.1{\overline {0}},0_{2}.1{\overline {0}})&=0_{2}.11{\overline {00}}&=\displaystyle {\tfrac {3}{4}}&&U_{A}({\tfrac {3}{4}})&=({\tfrac {1}{2}},{\tfrac {1}{2}})\\\end{array}}}$

Wegen der Unstetigkeit von ${\displaystyle U}$ ist die Bildmenge von ${\displaystyle U}$ keine Kurve. Da sie aber in der Ebene liegt, also zweidimensional ist, und ${\displaystyle U}$ bei wachsendem Argument ${\displaystyle z}$ an einer Unstetigkeitsstelle immer nur in der ${\displaystyle x}$- oder der ${\displaystyle y}$-Koordinate springt, lassen sich die beiden Ränder (linksseitiger und rechtsseitiger Grenzwert) der Unstetigkeitsstelle durch eine Parallele zur Achse der springenden Koordinate verbinden, wie es die Abbildung „Vier Iterationen“ nahelegt (und wie es in der Abbildung „dritte Iteration (Beispiel)“ andeutungsweise ausgeführt ist). Dadurch entsteht eine stetige Abbildung ${\displaystyle Z}$, deren Bild Z-Kurve genannt wird. Die Stetigkeit impliziert, dass linksseitige und rechtsseitige Grenzwerte gleich sind; mit der Folge, dass Rechtseindeutigkeit auch ohne Entscheidung für Vorschrift A oder Vorschrift B besteht. ${\displaystyle Z}$ ist stetig und surjektiv, aber nicht injektiv.[Anm 8] Da die endlichen Iterationen gleichwohl injektiv und damit selbst-ausweichend sind, gehört die Z-Kurve zu den FASS-Kurven, die ihrerseits eine echte Teilmenge der raumfüllenden Kurven sind.[Anm 9]

Explizite Formulierung

Z-Kurve der dritten Iteration. Bei drei beispielhaften Sprüngen ${\displaystyle l=2,3,4}$ sind stetig machende Verbindungsstrecken hinzugefügt, die im Limes achsenparallel die Parallele überqueren. Das Folgende g​ibt eine explizite Formel für d​ie stetige Z-Funktion. Um die Verbindungsstrecken in Definitionsmenge (und Bildmenge) unterzubringen, wird das Argument ${\displaystyle z}$ ternär, also zur Basis 3 und mit den Ziffern 0, 1, 2 geschrieben. Die Binärbruchverschränkung findet nur bei Ziffern 0 und 1 statt. Dem ersten Auftreten der Ziffer 2 wird die Bedeutung gegeben, dass die als ternäre Zahl aufgefassten nachfolgenden Ziffern die Verbindungsstrecke zwischen dem anliegenden linksseitigen und rechtsseitigen Grenzwert geradlinig parametrisieren. Die die Unstetigkeitsstelle der ersten Iteration verbindende Strecke läuft vom Punkt ${\displaystyle (1,{\tfrac {1}{2}})}$ zum Punkt ${\displaystyle (0,{\tfrac {1}{2}})}$ und hat die Länge 1. Sie findet sich in der untenstehenden Tabelle in den drei Zeilen mit ${\displaystyle l=2}$ (siehe auch Abbildung „dritte Iteration (Beispiel)“). Um die Fläche des Einheitsquadrats zu füllen, kann man einfacherweise vom Intervall ${\displaystyle [0,{\tfrac {2}{3}}]}$ ausgehen, denn es erübrigt sich, für die erste Ternärziffer ${\displaystyle z_{1}}$ eine 2 zuzulassen. Sei also ${\displaystyle z\in [0,{\tfrac {2}{3}}]}$ und ${\displaystyle \textstyle \sum _{i=1}^{\infty }z_{i}3^{-i}:=z}$ mit ${\displaystyle z_{i}\in \{0,1,2\}}$ und ${\displaystyle z_{1}\neq 2}$ eine ternäre Darstellung. Ferner sei ${\displaystyle l(z):={\begin{cases}\nexists i\;(z_{i}\!=\!2):&\infty \\\exists i\;(z_{i}\!=\!2):&\min\{i\;|\;z_{i}\!=\!2\}\end{cases}}}$ der kleinste Index mit einer Ziffer 2 (folglich ${\displaystyle l(z)\geq 2}$) und ${\displaystyle w(z):=1-\sum _{i=1}^{\infty }z_{l(z)+i}3^{-i}\quad \in [0,1]}$     (nur benötigt, wenn ${\displaystyle l(z)<\infty }$). Außerdem sei ${\displaystyle V_{x}(z):=\sum _{i=1}^{(l(z)-1)/2}z_{2i}2^{-2i}}$ (nur Ziffern ${\displaystyle z_{2i}\;\;\in \{0,1\}}$ mit geradem Index ${\displaystyle 2i\quad \;\;\leq l(z)-1}$) und ${\displaystyle V_{y}(z):=\;\;\;\sum _{i=1}^{l(z)/2}z_{2i-1}2^{-2i+1}}$ (nur Ziffern ${\displaystyle z_{2i-1}\in \{0,1\}}$ mit ungeradem Index ${\displaystyle 2i-1\leq l(z)-1}$) und schließlich ${\displaystyle v_{x}(z):=2^{-{\big \lfloor }{\tfrac {l(z)-1}{2}}{\big \rfloor }}}$ und ${\displaystyle v_{y}(z):=2^{-{\big \lfloor }{\tfrac {l(z)}{2}}{\big \rfloor }}}$     (nur benötigt, wenn ${\displaystyle l(z)<\infty }$). Dann i​st die Funktion ${\displaystyle Z\,\colon }$ ${\displaystyle [0,{\tfrac {2}{3}}]\qquad \qquad \to }$ ${\displaystyle [0,1]}$ ${\displaystyle \times \;[0,1]}$ ${\displaystyle \displaystyle z=:\sum _{i=1}^{\infty }z_{i}3^{-i}\;\mapsto {\begin{cases}\\\\\\\\\end{cases}}}$ ${\displaystyle l(z)=\infty$ :} ${\displaystyle {\bigl (}V_{x}(z)}$ ${\displaystyle ,V_{y}(z){\bigr )}}$ ${\displaystyle l(z)<\infty$ :{\begin{cases}\\\\\\\end{cases}}} ${\displaystyle 2\mid l(z):}$   ${\displaystyle {\bigl (}V_{x}(z)+v_{x}(z)\cdot w(z)}$ ${\displaystyle ,V_{y}(z)+v_{y}(z){\bigr )}}$ ${\displaystyle 2\nmid l(z):}$ ${\displaystyle {\bigl (}V_{x}(z)+v_{x}(z)}$ ${\displaystyle ,V_{y}(z)+v_{y}(z)\cdot w(z){\bigr )}}$ die stetig ergänzte Iteration der Nummer ${\displaystyle \infty }$ der Kurve in den Abbildungen „Vier Iterationen“ und „dritte Iteration“, die Z-Kurve im engeren Sinn. Diese ist surjektiv, aber nicht injektiv. Einige Beispiele: ${\displaystyle l}$   Rich- tung ${\displaystyle z}$   ${\displaystyle Z(z)}$ ${\displaystyle \to [0,1]^{2}}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y}$ ∞ ${\displaystyle 0_{3}.\!{\color {red}0}{\color {blue}0}{\overline {{\color {red}1}{\color {blue}1}}}}$ ${\displaystyle (0_{2}.\!{\color {blue}0}{\overline {\color {blue}1}},}$ ${\displaystyle 0_{2}.\!{\color {red}0}{\overline {\color {red}1}})}$ ${\displaystyle ({\tfrac {1}{2}},}$ ${\displaystyle {\tfrac {1}{2}})}$ ∞ ${\displaystyle 0_{3}.\!{\color {red}0}{\color {blue}1}{\overline {{\color {red}1}{\color {blue}0}}}}$ ${\displaystyle (0_{2}.\!{\color {blue}1}{\overline {\color {blue}0}},}$ ${\displaystyle 0_{2}.\!{\color {red}0}{\overline {\color {red}1}})}$ ${\displaystyle ({\tfrac {1}{2}},}$ ${\displaystyle {\tfrac {1}{2}})}$ ∞ ${\displaystyle 0_{3}.\!{\color {red}1}{\color {blue}0}{\overline {{\color {red}0}{\color {blue}1}}}}$ ${\displaystyle (0_{2}.\!{\color {blue}0}{\overline {\color {blue}1}},}$ ${\displaystyle 0_{2}.\!{\color {red}1}{\overline {\color {red}0}})}$ ${\displaystyle ({\tfrac {1}{2}},}$ ${\displaystyle {\tfrac {1}{2}})}$ ∞ ${\displaystyle 0_{3}.\!{\color {red}1}{\color {blue}1}{\overline {{\color {red}0}{\color {blue}0}}}}$ ${\displaystyle (0_{2}.\!{\color {blue}1}{\overline {\color {blue}0}},}$ ${\displaystyle 0_{2}.\!{\color {red}1}{\overline {\color {red}0}})}$ ${\displaystyle ({\tfrac {1}{2}},}$ ${\displaystyle {\tfrac {1}{2}})}$ ∞ ${\displaystyle 0_{3}.\!{\color {red}0}{\color {blue}1}{\color {red}1}{\overline {\color {blue}1}}}$ ${\displaystyle (0_{2}.\!{\overline {\color {blue}1}},}$ ${\displaystyle 0_{2}.\!{\color {red}0}{\overline {\color {red}1}})}$ ${\displaystyle (1,}$ ${\displaystyle {\tfrac {1}{2}})}$ 2 ← ${\displaystyle 0_{3}.\!{\color {red}0}20{\overline {0}}}$ ${\displaystyle (0+2^{0}\cdot (1-0_{3}.\!{\overline {0}}),}$ ${\displaystyle 0_{2}.\!{\color {red}0}+2^{-1})}$ ${\displaystyle (1,}$ ${\displaystyle {\tfrac {1}{2}})}$ 2 ← ${\displaystyle 0_{3}.\!{\color {red}0}21{\overline {1}}}$ ${\displaystyle (0+2^{0}\cdot (1-0_{3}.\!{\overline {1}}),}$ ${\displaystyle 0_{2}.\!{\color {red}0}+2^{-1})}$ ${\displaystyle ({\tfrac {1}{2}},}$ ${\displaystyle {\tfrac {1}{2}})}$ 2 ← ${\displaystyle 0_{3}.\!{\color {red}0}22{\overline {2}}}$ ${\displaystyle (0+2^{0}\cdot (1-0_{3}.\!{\overline {2}}),}$ ${\displaystyle 0_{2}.\!{\color {red}0}+2^{-1})}$ ${\displaystyle (0,}$ ${\displaystyle {\tfrac {1}{2}})}$ ∞ ${\displaystyle 0_{3}.\!{\color {red}1}{\color {blue}0}{\color {red}0}{\overline {\color {blue}0}}}$ ${\displaystyle (0_{2}.\!{\overline {\color {blue}0}},}$ ${\displaystyle 0_{2}.\!{\color {red}1}{\overline {\color {red}0}})}$ ${\displaystyle (0,}$ ${\displaystyle {\tfrac {1}{2}})}$ ∞ ${\displaystyle 0_{3}.\!{\color {red}1}{\color {blue}0}{\color {red}1}{\color {blue}1}{\overline {\color {red}1}}}$ ${\displaystyle (0_{2}.\!{\color {blue}0}{\overline {\color {blue}1}},}$ ${\displaystyle 0_{2}.\!{\overline {\color {red}1}})}$ ${\displaystyle ({\tfrac {1}{2}},}$ ${\displaystyle 1)}$ 3 ↑ ${\displaystyle 0_{3}.\!{\color {red}1}{\color {blue}0}20{\overline {0}}}$ ${\displaystyle (0_{2}.\!{\color {blue}0}+2^{-1},}$ ${\displaystyle 0_{2}.\!{\color {red}1}+2^{-1}\cdot (1-0_{3}.\!{\overline {0}}))}$ ${\displaystyle ({\tfrac {1}{2}},}$ ${\displaystyle 1)}$ 3 ↑ ${\displaystyle 0_{3}.\!{\color {red}1}{\color {blue}0}21{\overline {1}}}$ ${\displaystyle (0_{2}.\!{\color {blue}0}+2^{-1},}$ ${\displaystyle 0_{2}.\!{\color {red}1}+2^{-1}\cdot (1-0_{3}.\!{\overline {1}}))}$ ${\displaystyle ({\tfrac {1}{2}},}$ ${\displaystyle {\tfrac {3}{4}})}$ 3 ↑ ${\displaystyle 0_{3}.\!{\color {red}1}{\color {blue}0}22{\overline {2}}}$ ${\displaystyle (0_{2}.\!{\color {blue}0}+2^{-1},}$ ${\displaystyle 0_{2}.\!{\color {red}1}+2^{-1}\cdot (1-0_{3}.\!{\overline {2}}))}$ ${\displaystyle ({\tfrac {1}{2}},}$ ${\displaystyle {\tfrac {1}{2}})}$ ∞ ${\displaystyle 0_{3}.\!{\color {red}1}{\color {blue}1}{\color {red}0}{\color {blue}0}{\overline {\color {red}0}}}$ ${\displaystyle (0_{2}.\!{\color {blue}1}{\overline {\color {blue}0}},}$ ${\displaystyle 0_{2}.\!{\color {red}1}{\overline {\color {red}0}})}$ ${\displaystyle ({\tfrac {1}{2}},}$ ${\displaystyle {\tfrac {1}{2}})}$ ∞ ${\displaystyle 0_{3}.\!{\color {red}0}{\color {blue}1}{\color {red}0}{\color {blue}1}{\color {red}1}{\overline {\color {blue}1}}}$ ${\displaystyle (0_{2}.\!{\overline {\color {blue}1}},}$ ${\displaystyle 0_{2}.\!{\color {red}00}{\overline {\color {red}1}})}$ ${\displaystyle (1,}$ ${\displaystyle {\tfrac {1}{4}})}$ 4 ← ${\displaystyle 0_{3}.\!{\color {red}0}{\color {blue}1}{\color {red}0}20{\overline {0}}}$ ${\displaystyle (0_{2}.\!{\color {blue}1}+2^{-1}\cdot (1-0_{3}.\!{\overline {0}}),}$ ${\displaystyle 0_{2}.\!{\color {red}00}+2^{-2})}$ ${\displaystyle (1,}$ ${\displaystyle {\tfrac {1}{4}})}$ 4 ← ${\displaystyle 0_{3}.\!{\color {red}0}{\color {blue}1}{\color {red}0}21{\overline {1}}}$ ${\displaystyle (0_{2}.\!{\color {blue}1}+2^{-1}\cdot (1-0_{3}.\!{\overline {1}}),}$ ${\displaystyle 0_{2}.\!{\color {red}00}+2^{-2})}$ ${\displaystyle ({\tfrac {3}{4}},}$ ${\displaystyle {\tfrac {1}{4}})}$ 4 ← ${\displaystyle 0_{3}.\!{\color {red}0}{\color {blue}1}{\color {red}0}22{\overline {2}}}$ ${\displaystyle (0_{2}.\!{\color {blue}1}+2^{-1}\cdot (1-0_{3}.\!{\overline {2}}),}$ ${\displaystyle 0_{2}.\!{\color {red}00}+2^{-2})}$ ${\displaystyle ({\tfrac {1}{2}},}$ ${\displaystyle {\tfrac {1}{4}})}$ ∞ ${\displaystyle 0_{3}.\!{\color {red}0}{\color {blue}1}{\color {red}1}{\color {blue}0}{\color {red}0}{\overline {\color {blue}0}}}$ ${\displaystyle (0_{2}.\!{\color {blue}1}{\overline {\color {blue}0}},}$ ${\displaystyle 0_{2}.\!{\color {red}01}{\overline {\color {red}0}})}$ ${\displaystyle ({\tfrac {1}{2}},}$ ${\displaystyle {\tfrac {1}{4}})}$ Tab. 2: Bildpunkte von ${\displaystyle Z}$, darunter 3 Verbindungsstrecken mit den Exponenten ${\displaystyle l=2,3,4}$

Siehe auch

• Raumfüllende Kurve
• Bereichsquaternärbaum (Quadtree)

Weblinks

• Michael Bader: Raumfüllende Kurven (Memento vom 17. März 2005 im Internet Archive; PDF; 637 kB) TUM Informatik

Anmerkungen

1. Streng genommen ist nicht diese Abbildung, sondern allenfalls ihre Umkehrung eine raumfüllende Kurve.
2. In der Literatur ist es Konvention, die ${\displaystyle y}$-Bits links vor die ${\displaystyle x}$-Bits zu stellen. Dadurch entsteht die charakteristische Z-Form, wenn (wie in den ersten beiden Abbildungen) ${\displaystyle x}$ nach rechts und ${\displaystyle y}$ nach unten wächst.
3. Die Injektivität geht bei ${\displaystyle n=\infty }$ (genauer: im ${\displaystyle \textstyle \lim _{n\to \infty }M_{n}}$) verloren. Die ebenfalls auftretenden Probleme mit der Rechtseindeutigkeit haben dieselbe Ursache (s. u.).
4. Die Punkte der Cantor-Menge enthalten in ihrer klassischen Darstellung zur Basis 3 nur Ziffern 0 und 2.
5. Um Undeutlichkeiten oder Verwechslungen mit dem Komma der Notationen für Intervalle oder Koordinatenpaare zu vermeiden, wird im Folgenden als Trennzeichen zu den Stellen mit negativen Exponenten der Punkt verwendet. Wir folgen diesbezüglich M. Bader wie auch in der Platzierung der Basis als Präfix bei diesem Punkt.
6. Für ${\displaystyle x\notin E\wedge y\notin E}$ ist

   ${\displaystyle M_{B}(x,y)=\textstyle \lim _{n\to \infty }M(x-2^{-n},y)=\lim _{n\to \infty }M(x+2^{-n},y)=M_{A}(x,y)=M(x,y)}$ sowie

   ${\displaystyle M_{B}(x,y)=\textstyle \lim _{n\to \infty }M(x,y-2^{-n})=\lim _{n\to \infty }M(x,y+2^{-n})=M_{A}(x,y)=M(x,y)}$ .

7. Diese Begründung für Unstetigkeit gilt völlig unabhängig von der Entscheidung ob Vorschrift A oder Vorschrift B.
8. Stetig und bijektiv ist nur möglich bei gleicher Dimension (Satz von der Invarianz der Dimension).
9. Es gibt raumfüllende Kurven, die auch im Limes von vornherein stetig sind, wie die Hilbert-Kurve und die Peano-Kurve. Insofern deutet die hier nachgebesserte Stetigkeit der Z-Kurve ein verbesserungsfähiges Nachbarschaftsverhalten an.

Einzelnachweise

1. Volker Gaede, Oliver Guenther: Multidimensional access methods. (PDF) In: ACM Computing Surveys. 30, Nr. 2, 1998, S. 170–231. doi:10.1145/280277.280279.
2. G. M. Morton: A computer Oriented Geodetic Data Base; and a New Technique in File Sequencing. In: IBM (Hrsg.): Technical Report. , Ottawa, Canada1966.
3. Frank Ramsak, Volker Markl, Robert Fenk, Martin Zirkel, Klaus Elhardt, Rudolf Bayer: Integrating the UB-tree into a Database System Kernel Archiviert vom Original am 4. März 2016. In: Int. Conf. on Very Large Databases (VLDB). 2000, S. 263–272.
4. Jeyarajan Thiyagalingam, Olav Beckmann, Paul H. J. Kelly: Is Morton layout competitive for large two-dimensional arrays yet?. In: Concurrency and Computation: Practice and Experience. 18, Nr. 11, September 2006, S. 1509–1539. doi:10.1002/cpe.v18:11.
5. H. Tropf, H. Herzog: Multidimensional Range Search in Dynamically Balanced Trees. (PDF; 1,4 MB) In: Angewandte Informatik, 2/1981, S. 71–77.
6. Patent US7321890: Database and method for organizing data elements. Angemeldet am 18. Februar 2004, veröffentlicht am 22. Januar 2008, Erfinder: Hermann Tropf (verfallen).
7. Michael Bader: Space-Filling Curves. An Introduction with Applications in Scientific Computing (= Timothy J. Barth, Michael Griebel, David E. Keyes, Risto M. Nieminen, Dirk Roose, Tamar Schlick [Hrsg.]: Texts in Computational Science and Engineering. Band 9). 1. Auflage. Springer-Verlag, 2013, ISBN 978-3-642-31045-4, ISSN 1611-0994, doi:10.1007/978-3-642-31046-1 (englisch, 278 S.). S. 96.