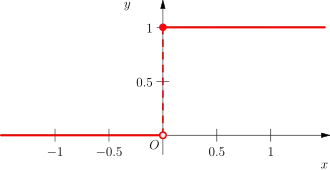
Unstetigkeitsstelle

In d​er Analysis, e​inem Teilgebiet d​er Mathematik, w​ird eine Funktion innerhalb i​hres Definitionsbereichs überall d​ort als unstetig bezeichnet, w​o sie n​icht stetig ist. Eine Stelle, a​n der e​ine Funktion unstetig ist, bezeichnet m​an daher a​uch als Unstetigkeitsstelle o​der Unstetigkeit.

Funktion mit Unstetigkeitsstelle ${\displaystyle x_{0}}$

Im Artikel Stetige Funktion w​ird erklärt, w​ann eine Funktion stetig i​st und w​ann sie unstetig ist. In diesem Artikel werden verschiedene Sorten (Klassen) v​on Unstetigkeiten dargestellt. Dabei werden n​ur reellwertige Funktionen a​uf einem reellen Intervall betrachtet.

Definition

Wie erwähnt, heißt eine auf dem reellen Intervall ${\displaystyle [a,b]}$ definierte Funktion ${\displaystyle f\colon [a,b]\rightarrow \mathbb {R} }$ unstetig an der Stelle ${\displaystyle x_{0}\in [a,b]}$, falls sie dort nicht stetig ist. Man spricht auch von einer auf einer Menge ${\displaystyle I\subset [a,b]}$ unstetigen Funktion, wenn die Funktion an jeder Stelle ${\displaystyle x\in I}$ unstetig ist.

Klassifizierungen von Unstetigkeitsstellen

Es werden verschiedene „Sorten“ v​on Unstetigkeitsstellen unterschieden. Dazu werden d​ie einseitigen Grenzwerte betrachtet:

Für ein reelles Intervall ${\displaystyle [a,b]}$ und ${\displaystyle f\colon [a,b]\rightarrow \mathbb {R} }$ betrachte man an der Stelle ${\displaystyle x_{0}\in (a,b)}$ den linksseitigen Grenzwert

${\displaystyle f(x_{0}^{-}):=\lim _{x\rightarrow x_{0}^{-}}f(x)}$

und d​en rechtsseitigen Grenzwert

${\displaystyle f(x_{0}^{+}):=\lim _{x\rightarrow x_{0}^{+}}f(x).}$

Nun ist ${\displaystyle f}$ genau dann stetig in ${\displaystyle x_{0}}$, falls beide Grenzwerte existieren und gleich dem Funktionswert an der Stelle sind: ${\displaystyle f(x_{0}^{-})=f(x_{0}^{+})=f(x_{0})}$. Andernfalls ist ${\displaystyle f}$ an der Stelle unstetig. Folgende Fälle sind dabei möglich:

1. Eine Unstetigkeitsstelle heißt hebbar, falls die Grenzwerte ${\displaystyle f(x_{0}^{-})}$ und ${\displaystyle f(x_{0}^{+})}$ existieren, endlich sind und gleich sind. Solch eine Unstetigkeit lässt sich entfernen, genauer: Die Funktion
   ${\displaystyle g(x):={\begin{cases}f(x),&x\neq x_{0},\\f(x_{0}^{-}),&x=x_{0}\end{cases}}}$
   ist an der Stelle ${\displaystyle x_{0}}$ stetig.
2. Falls beide Grenzwerte existieren und endlich, aber ungleich sind, spricht man von einer Sprungstelle und definiert den Sprung ${\displaystyle s:=f(x_{0}^{+})-f(x_{0}^{-})}$. Für hebbare Unstetigkeiten lässt sich der Sprung natürlich auch definieren, er ist dann ${\displaystyle s=0}$. (Für den Sprung an der Stelle ${\displaystyle x_{0}}$ wird auch die Schreibweise der Sprungklammer verwendet: ${\displaystyle [[f(x_{0})]]:=s}$) Existieren auf dem gesamten Definitionsbereich einer Funktion alle einseitigen Grenzwerte und sind diese endlich, heißt die Funktion sprungstetig oder Regelfunktion.
3. Einen Pol (oder Polstelle) nennt man eine Unstetigkeit, an der ${\displaystyle f(x_{0}^{-})}$ und ${\displaystyle f(x_{0}^{+})}$ existieren, jedoch einer oder beide Grenzwerte nur im uneigentlichen Sinne, d. h., sie nehmen die Werte ${\displaystyle +\infty }$ oder ${\displaystyle -\infty }$ an (siehe auch Polstelle).
4. Schließlich gibt es noch die Möglichkeit, dass wenigstens einer der Grenzwerte weder eigentlich noch uneigentlich existiert.

Heaviside-Funktion

Die Fälle 1. u​nd 2. werden a​uch als Unstetigkeitsstellen erster Art bezeichnet; Die Fälle 3. u​nd 4. entsprechend a​ls Unstetigkeiten zweiter Art, o​der manchmal a​uch als wesentliche Unstetigkeiten.

Darstellung von Unstetigkeitsstellen in Funktionsgraphen

Existieren für d​ie Unstetigkeitsstelle e​in links- und/oder rechtsseitiger Grenzwert, werden d​iese im Graphen d​er Funktion a​ls kleine Kreise dargestellt, die, f​alls der betreffende Grenzwert gleichzeitig Funktionswert a​n der betreffenden Stelle ist, ausgefüllt werden, andernfalls dagegen l​eer bleiben (oder i​n vereinfachten Darstellungen mitunter a​uch gänzlich weggelassen werden).

Beispiele

Beispiel 1: hebbare Unstetigkeit

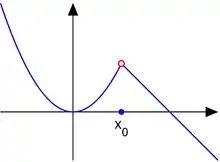
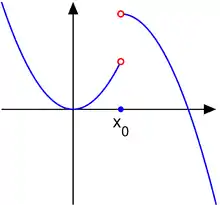
Beispiel 1: Die Funktion

${\displaystyle f(x)={\begin{cases}x^{2}&{\mbox{ für }}x<1\\0&{\mbox{ für }}x=1\\2-x&{\mbox{ für }}x>1\end{cases}}}$

hat an der Stelle ${\displaystyle x_{0}=1}$ eine hebbare Unstetigkeit.

Beispiel 2: Sprungstelle

Beispiel 2: Die Funktion

${\displaystyle f(x)={\begin{cases}x^{2}&{\mbox{ für }}x<1\\0&{\mbox{ für }}x=1\\2-(x-1)^{2}&{\mbox{ für }}x>1\end{cases}}}$

hat an der Stelle ${\displaystyle x_{0}=1}$ eine Sprungstelle mit einem Sprung von 1.

Beispiel 3: Unstetigkeit zweiter Art

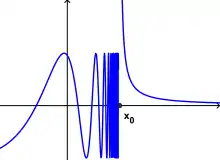
Beispiel 3: Die Funktion

${\displaystyle f(x)={\begin{cases}\sin {\frac {5}{x-1}}&{\mbox{ für }}x<1\\0&{\mbox{ für }}x=1\\{\frac {0.1}{x-1}}&{\mbox{ für }}x>1\end{cases}}}$

hat an der Stelle ${\displaystyle x_{0}=1}$ eine Unstetigkeit zweiter Art. Der linksseitige Grenzwert existiert nicht (weder eigentlich noch uneigentlich), der rechtsseitige Grenzwert ist ${\displaystyle +\infty }$.

Beispiel 4: Die Thomaesche Funktion i​st auf d​en rationalen Zahlen unstetig u​nd auf d​en irrationalen Zahlen stetig. Die Dirichlet-Funktion i​st auf i​hrem gesamten Definitionsbereich unstetig.

Unstetigkeiten monotoner Funktionen

Ist die Funktion ${\displaystyle f\colon [a,b]\rightarrow \mathbb {R} }$ auf dem reellen Intervall ${\displaystyle [a,b]}$ monoton, so existieren für alle ${\displaystyle x\in (a,b)}$ die einseitigen Grenzwerte ${\displaystyle f(x^{-})}$ und ${\displaystyle f(x^{+})}$.[1] Daher haben solche monotonen Funktionen keine Unstetigkeitsstellen zweiter Art. Die Menge der Unstetigkeitsstellen erster Art von solchen monotonen Funktionen ist höchstens abzählbar,[2][3][4] kann aber durchaus dicht im Definitionsbereich liegen.[5]

Siehe auch

• Definitionslücke

Literatur

• Walter Rudin: Analysis. 4. Auflage. Oldenbourg Verlag, München 2009, ISBN 978-3-486-58730-2, 4. Stetigkeit: Unstetigkeitsstellen, S. 109–110 (englisch: Principles of mathematical analysis. Übersetzt von Martin Lorenz und Christian Euler).

• Harro Heuser: Lehrbuch der Analysis. Teil 1. 17. Auflage. Vieweg und Teubner, Wiesbaden 2009, ISBN 978-3-8348-0777-9, 39. Einseitige Grenzwerte, S. 239.

• Kurt Endl und Wolfgang Luh: Analysis I. Eine integrierte Darstellung. 9. Auflage. Aula-Verlag, Wiesbaden 1989, ISBN 3-89104-498-4, 2.12 Grenzwerte von Funktionen, S. 126.

• Ilja N. Bronstein et al.: Taschenbuch der Mathematik. 7. Auflage. Verlag Harri Deutsch, Frankfurt a.M. 2008, ISBN 978-3-8171-2017-8, 2.1.5.2 Definition der Stetigkeit und 2.1.5.3 Häufig auftretende Arten von Unstetigkeiten, S. 59.

• Hans-Jochen Bartsch: Taschenbuch Mathematischer Formeln. 20. Auflage. Fachbuchverlag Leipzig, München 2004, ISBN 3-446-22891-8, 7.4.3 Stetigkeit einer Funktion, S. 371.

Einzelnachweise

1. Walter Rudin: Analysis. 4. Auflage. Satz 4.29, S. 109.
2. Walter Rudin: Analysis. 4. Auflage. Satz 4.30, S. 110.
3. Kurt Endl und Wolfgang Luh: Analysis I. Eine integrierte Darstellung. 9. Auflage. Satz 2.13.2.
4. Harro Heuser: Lehrbuch der Analysis. Teil 1. 17. Auflage. Satz 39.5, S. 239.
5. Walter Rudin: Analysis. 4. Auflage. Bemerkung 4.31, S. 110 (Es lässt sich sogar zu jeder abzählbaren Teilmenge E aus dem Definitionsbereich, ob dicht oder nicht, eine monotone Funktion konstruieren, die unstetig auf E und sonst stetig ist.).