Bitweiser Operator
In der Informatik ist ein bitweiser Operator ein Operator, der auf ein oder zwei Bitketten, Bitfeldern, Bitfolgen oder Bitvektoren auf der Ebene der einzelnen Bits angewendet wird. Insbesondere in den Programmiersprachen der C-Familie können Binärzahlen ohne weitere syntaktische Kennzeichnung als Bitfolgen aufgefasst werden.
Die zugrunde liegenden Operationen auf den einzelnen Bits sind schaltungstechnisch die allereinfachsten, und alle höheren Operationen lassen sich auf sie zurückführen. Die bitweisen Operationen werden wegen ihrer geringeren Bedeutung für die Geschwindigkeit eines Computersystems jedoch meist weniger durch Optimierung bevorzugt als die komplexeren arithmetischen Operationen wie Addition und Subtraktion.
Bitweise Operatoren
Die Sprechweise bitweise deutet darauf hin, dass die mehrgliedrigen Eingabeoperanden komponentenweise verarbeitet werden. (Sie können natürlich auch eingliedrig sein.) Man kann davon ausgehen, dass bei zweistelligen Operationen verschieden lange Operanden vom Kompiler als Fehler angesehen werden.
In vielen Programmiersprachen der C-Familie wird syntaktisch und semantisch zwischen bitweise (= mehrgliedrig und komponentenweise) und logisch (= boolesch = eine einzige Komponente) unterschieden. Letztere werden wegen der naheliegenden Verwechslungsgefahr in diesem Artikel zusätzlich aufgeführt.
NICHT
Das bitweise NICHT oder Komplement ist eine einstellige Verknüpfung, die eine logische Negation (Inversion) jedes Bits durchführt. Wird die Bitfolge als Binärzahl aufgefasst, dann ist dies die Bildung des Einerkomplements. Jede 0 wird durch eine 1 ausgetauscht und umgekehrt. Beispiel:
NICHT 0111
= 1000
In vielen Programmiersprachen der C-Familie wird das bitweise NICHT als ~ (Tilde) dargestellt.
Im Gegensatz dazu wird beim logischen Operator ! (Ausrufezeichen) für logisches NICHT der gesamte Wert als Boolescher Ausdruck true ≠ 0 oder false = 0 interpretiert. Das logische NICHT ist keine bitweise Operation.
NICHT (bitweise): ~0 = 1
~1dez = 0dez
~5dez = ~0101bin = 1010bin = 10dez
NICHT (logisch): !false = true
!true = false
!0 = true
!1dez = false
!5dez = false
UND
Das bitweise UND wird auf zwei Bitfolgen gleicher Länge angewendet und gibt eine Bitfolge derselben Länge zurück, indem es jeweils Bits an der gleichen Stelle (jeweils das erste Bit, jeweils das zweite Bit usw.) mit einem logischen UND (logische Konjunktion) verknüpft. Bei jedem Paar ist das Ergebnisbit 1, falls beide Bits 1 sind, ansonsten 0. Beispiel:
0101 UND 0011 = 0001
In den mit C verwandten Programmiersprachen wird das bitweise UND durch & (kaufmännisches Und, engl. ampersand) dargestellt. Das boolesche Gegenstück dazu, das logische UND, interpretiert jeden seiner zwei Operanden als einen booleschen Wert und wird als && (zwei kaufmännische Und) dargestellt.
Das bitweise UND kann verwendet werden, um eine Bitfolge zu maskieren. Dadurch können Teile eines Bitstrings isoliert werden, und man kann ermitteln, ob ein bestimmtes Bit gesetzt ist oder nicht. Beispiel:
0011
Um herauszufinden, ob das dritte Bit gesetzt ist oder nicht, wird darauf ein bitweises UND mit einer Maske angewendet, die an der dritten Position eine 1 enthält:
0011 UND 0010 = 0010
Da das Ergebnis nicht Null ist, muss das dritte Bit in der ursprünglichen Bitfolge eine 1 gewesen sein. Diese Anwendung des bitweisen UND wird bitweise Maskierung genannt, weil Teile, die nicht geändert werden sollen oder für die Berechnung nicht wichtig sind, ausgeblendet werden.
Das bitweise UND kann mit dem bitweisen NICHT kombiniert werden, um Bits zu löschen. Beispielsweise soll in der Bitfolge
0110
das zweite Bit gelöscht (d. h. auf 0 gesetzt) werden, sodass im Ergebnis 0010 herauskommt.
Dies geschieht, indem wir eine invertierte Maske (die Null muss dafür an der Stelle der zu ändernden Ziffer gesetzt werden) auf unsere Bitfolge anwenden. Invertieren können wir mit dem NICHT-Operator.
NICHT 0100
= 1011
Danach wird die Bitfolge und die Maske mittels UND-Operator verknüpft:
0110
UND 1011
= 0010
Weiterhin ist es mit dem bitweisen UND möglich, eine Binärzahl modulo 2k zu rechnen, indem man sie mit 2k−1 UND-verknüpft. Dadurch werden alle Bits ab der k-ten Position von rechts auf 0 gesetzt.
Beispiel: 17 mod 8 = 1 entspricht
010001 (17)
UND 000111 (7 = 8−1)
= 000001
ODER
Das bitweise ODER wird auf zwei Bitfolgen gleicher Länge angewendet und gibt eine Bitfolge derselben Länge zurück, indem es jeweils Bits an der gleichen Stelle mit einem logischen ODER (logische Disjunktion) verknüpft. Bei jedem Paar ist das Ergebnisbit 0, falls beide Bits 0 sind, ansonsten ist das Ergebnisbit 1. Beispiel:
0101 ODER 0011 = 0111
In den mit C verwandten Programmiersprachen wird das bitweise ODER durch | (senkrechter Strich) dargestellt. Das boolesche Gegenstück dazu, das logische ODER, das seine Operanden als boolesche Werte interpretiert, wird als || (zwei senkrechte Striche) dargestellt.
Das bitweise ODER wird verwendet, wenn mehrere Bits als Flags verwendet werden; die Bits einer einzelnen Binärzahl können jeweils eine eigene boolesche Variable darstellen. Wendet man das bitweise ODER auf einen solchen Binärwert und eine „Maske“ an, die an bestimmten Stellen eine 1 enthält, so erhält man eine neue Bitfolge, in der diese Bits zusätzlich zu den ursprünglich vorhandenen gesetzt sind. Beispiel:
0010
kann als Liste von vier Flags angesehen werden. Das erste, zweite und vierte Flag sind nicht gesetzt (0), das dritte Flag ist gesetzt (1). Das erste Flag kann gesetzt werden, indem man diese Bitfolge mit einer Bitfolge verknüpft, die nur an der ersten Stelle eine 1 hat:
0010 ODER 1000 = 1010
Diese Technik wird eingesetzt, um Speicherplatz zu sparen, wenn Programme sehr viele Boolesche Werte verwalten müssen.
XOR

Das bitweise exklusive ODER wird auf zwei Bitfolgen der gleichen Länge angewendet und gibt eine Bitfolge derselben Länge zurück, indem es die logische XOR-Operation auf jedem Paar korrespondierender Bits durchführt. Das Ergebnisbit ist 1, falls die zwei Bits unterschiedlich sind, und 0, falls sie gleich sind. Beispiel:
0101 XOR 0011 = 0110
In den mit C verwandten Programmiersprachen wird das bitweise XOR als ^ (Circumflex) dargestellt. Das boolesche Gegenstück dazu, das logische XOR, das seine zwei Operanden jeweils als einen booleschen Wert auffasst, wird als ^^ dargestellt.
In der Assemblersprache wird das bitweise XOR gelegentlich eingesetzt, um den Wert eines Prozessorregisters auf 0 zu setzen. Wendet man XOR auf zwei identische Operanden an, so erhält man immer 0. In vielen Architekturen benötigt diese Operation weniger Rechenzeit, als man für das Laden einer 0 und das Speichern im Register benötigt.
Das bitweise XOR kann auch verwendet werden, um Flags in Bitfolgen umzuschalten.
Dazu fasst man den zweiten Operanden als NICHT-„Maske“ auf den ersten Operanden auf, die diejenigen Stellen logisch invertiert, an denen eine 1 steht, und die anderen unverändert lässt. Im Beispiel
0101 XOR 0011 („Maske“) = 0110
wird das dritte und vierte Flag umgeschaltet. Diese Technik kann eingesetzt werden, um Bitfolgen zu manipulieren, die mehrere boolesche Variablen repräsentieren.
Bitweise Verschiebungen
Bei den bitweisen Verschiebungen (engl. bitwise shift) werden die Bits als einzelne Zeichen an einer bestimmten Bit-Position aufgefasst – und nicht als Paare korrespondierender Bits wie in den oben stehenden Operationen. Dabei bedeutet das Kollektiv der Bits bei der arithmetischen Verschiebung eine Binärzahl oder bei der – etwas elementareren – logischen Verschiebung eine Bitkette (resp. eine vorzeichenlose (engl. unsigned) Binärzahl). Der Hauptunterschied besteht in der Behandlung des eventuellen Vorzeichenbits. Schaltungstechnisch können bitweise Verschiebungen und Rotationen um eine beliebige Stellenanzahl in Form von Barrel-Shiftern realisiert werden.
Bei diesen Operationen werden die Binär-Zeichen um eine angegebene Anzahl von Bitpositionen nach links oder rechts verschoben. Die Richtungsangabe wird dabei unabhängig von der Rechnerarchitektur (und deren Endianness) immer in der (big-endian) Standardkonvention des Dualsystems verstanden: Links bedeutet Multiplikation und rechts Division mit einer Zweierpotenz. Register der Prozessoren sowie Datentypen der Programmiersprachen beherbergen eine definierte endliche Anzahl von Bits, weshalb die spezifizierte Anzahl an Bits an einem Ende aus dem Register oder Datum „hinausgeschoben“, während die gleiche Anzahl am anderen Ende „hineingeschoben“ („hereingezogen“) wird.
Auf diese Weise induzieren die bitweisen Verschiebungsoperationen eine Adressierung der Bits innerhalb eines Bytes.
- Beispiel
Symbolik:
- „<<“ (in einigen Sprachen „shl“) Verschieben nach links, um den jeweils dahinter angegebenen Wert
- „>>“ (in einigen Sprachen „shr“) Verschieben nach rechts, um den jeweils dahinter angegebenen Wert
In Sprachen wie C wird für Rechtsverschiebungen abhängig vom Datentyp und ggf. Vorzeichen entweder mit Nullen (unsigned oder nicht-negativ) oder mit Einsen (signed und kleiner als Null) aufgefüllt. Andere Programmiersprachen (wie z. B. Java) verwenden stattdessen einen eigenen Operator >>>, bei dem stets mit Nullen aufgefüllt wird:
00111100 << 1 = 01111000 00111100 << 2 = 11110000 (signed erzeugt einen arithmetischen Überlauf) 11111100 << 2 = 11110000 (signed ohne arithmetischen Überlauf) 01001111 >> 1 = 00100111 11110000 >> 2 = 11111100 (signed) 11110000 >> 2 = 00111100 (unsigned) 11110000 >>> 2 = 00111100 (signed und unsigned) 01001111 >>> 1 = 00100111 (signed und unsigned)
Eine logische (oder arithmetische) Verschiebung um (Bitpositionen) nach links ist äquivalent zu einer Multiplikation mit , sofern keine 1-Bits hinaus- (bzw. in die Vorzeichenposition hinein)geschoben werden. Eine arithmetische Verschiebung um (Bitpositionen) nach rechts ist äquivalent zu einer Division durch ; hinausgeschobene 1-Bits gehen verloren.
00001100 << 2 = 00110000
Dieses Verfahren stellt somit eine Alternative zur Multiplikation bzw. Division mit Zweierpotenzen dar. Divisionsergebnisse werden abgeschnitten. Ebenfalls ist es möglich, eine n-Bit-Zahl modulo 2k zu rechnen, indem sie um jeweils n–k nach links und wieder nach rechts verschiebt. Etwas schneller noch kann man die modulo-Berechnung über das bitweise UND mit 2k–1 durchführen.
Eine Verschiebung um 0 Bitpositionen ändert den Wert nicht („identische Abbildung“). Ist für die Verschiebung um Bitpositionen definiert, dann gilt sowohl für (beidesmal) logische wie für (beidesmal) arithmetische Verschiebungen die „Hintereinanderausführung“:
((xyz) >> m) >> n = (xyz) >> (m+n) (signed und unsigned) ((xyz) << m) << n = (xyz) << (m+n) (signed und unsigned)
D. h.: Abgesehen von der Einschränkung über die Maximalzahl der Schiebepositionen, ab der das Verhalten (implementierungsabhängig und) undefiniert sein kann, genügt es, das Verhalten der Schiebeoperationen für eine (einzige) Schiebeposition zu definieren.
Logische Verschiebung
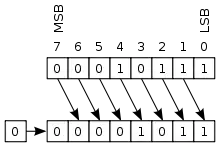 Logischer Rechtsshift |
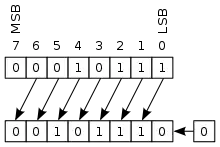 Logischer Linksshift |
Bei einer logischen Verschiebung (engl. logic shift) werden die hinausgeschobenen Bits verworfen und Nullen nachgezogen, unabhängig von Schieberichtung und Vorzeichen. Deshalb sind logische und arithmetische Verschiebung nach links (bis auf die eventuelle Setzung von Flags) identische Operationen. Bei der logischen Verschiebung nach rechts werden jedoch Nullen statt Kopien des Vorzeichenbits eingefügt. Daher wird die logische Verschiebung bei Bitketten oder vorzeichenlosen Binärzahlen eingesetzt, während arithmetische Verschiebungen bei vorzeichenbehafteten Zweierkomplementzahlen verwendet werden.
Arithmetische Verschiebung
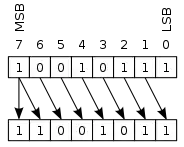 Arithmetischer Rechtsshift |
 Arithmetischer Linksshift |
Im Gegensatz zur logischen Verschiebung hat bei der arithmetischen (manchmal auch algebraischen) Verschiebung (engl. arithmetic shift) das höchstwertige Bit die Rolle des Vorzeichens (in der Darstellung als Zweierkomplement). Der zugrunde liegende Datentyp ist die vorzeichenbehaftete (signed) binäre Ganzzahl, für die der Compiler den arithmetischen Shift generiert. Hinausgeschobene Bits gehen verloren. Bei einer Verschiebung nach rechts werden Kopien des Vorzeichenbits an der Vorzeichenstelle eingeschoben (engl. sign propagation); bei einer Verschiebung nach links werden auf der rechten Seite Nullen nachgezogen. Beispiel (4-Bit-Register):
1100 RECHTS-SHIFT um 1 = 1110
0110 LINKS-SHIFT um 1 = 1100
Bei der Rechtsverschiebung wird das niedrigstwertige (das in der konventionellen Binärdarstellung am weitesten „rechts“ stehende, das Einer-) Bit hinausgeschoben und das höchstwertige Bit (MSB), das „Vorzeichenbit“, am hochwertigen („linken“) Ende erneut eingefügt, wodurch das Vorzeichen der Zahl erhalten bleibt. Bei der Linksverschiebung wird eine neue 0 am niedrigwertigen („rechten“) Ende eingefügt und das höchstwertige Bit aus dem Register hinausgeschoben. Ist das neue Vorzeichenbit verschieden vom zuletzt hinausgeschobenen (wechselt also das Vorzeichen beim letzten Schiebevorgang), dann wird in vielen Rechnerfamilien das Überlauf- oder Carry-Flag gesetzt, andernfalls gelöscht.
Eine arithmetische Verschiebung um (Bitpositionen) nach links ist äquivalent zu einer Multiplikation mit (sofern kein Überlauf auftritt). Eine arithmetische Verschiebung einer vorzeichenbehafteten (signed) Binärzahl (Zweierkomplementzahl) um nach rechts entspricht einer ganzzahligen Division durch mit Rundung auf die nächstkleinere Zahl – Beispiele: 1>>1 == 1>>31 == 0 und (-1)>>1 == (-1)>>31 == -1.
Zyklische Verschiebung ohne Übertragsbit
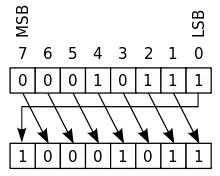 Zyklischer Rechtsshift |
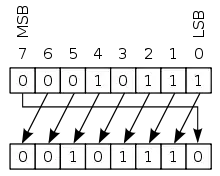 Zyklischer Linksshift |
Eine andere Form der bitweisen Verschiebung ist die zyklische Verschiebung (engl. circular shift) oder bitweise Rotation. Bei dieser Operation „rotieren“ die Bits, als ob das linke und das rechte Ende verbunden wären. Das Bit, das hineingeschoben wird, hat denselben Wert wie das Bit, das aus dem Register hinausgeschoben wird. Diese Operation erhält alle existierenden Bits und wird in einigen Verfahren der digitalen Kryptographie eingesetzt, beispielsweise beim AES-Verfahren, von und nach seinen Entwicklern auch „Rijndael“ genannt. In elementarer Form, jedoch nicht auf Bitebene, sondern auf der Basis eines Alphabets, wird sie in der Verschiebechiffre angewendet.
Zyklische Verschiebung mit Übertragsbit
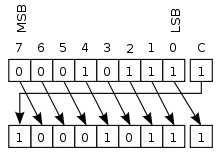 Zyklischer Rechtsshift mit Übertragsbit C (Carry) |
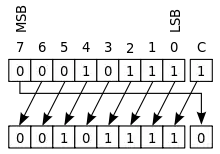 Zyklischer Linksshift mit Übertragsbit C (Carry) |
Zyklische Verschiebung mit Übertragsbit (engl. rotate through carry) funktioniert ähnlich wie die zyklische Verschiebung ohne Übertragsbit, jedoch werden die beiden Enden des Registers behandelt, als ob sie durch das Übertragsbit getrennt werden. Das Carry-Bit wird in das Register hineingeschoben, das aus dem Register hinausgeschobene Bit wird zum neuen Übertragsbit.
Eine einzelne zyklische Verschiebung mit Übertragsbit kann eine logische oder arithmetische Verschiebung um eine Stelle simulieren, wenn das Übertragsbit vorher entsprechend gesetzt wird. Enthält das Übertragsbit beispielsweise eine 0, dann entspricht die Verschiebung nach rechts einer arithmetischen Verschiebung nach rechts. Aus diesem Grund sind bei manchen Mikroprozessoren wie dem PICmicro nur Befehle für die beiden zyklischen Verschiebungsoperationen implementiert, es gibt keine speziellen Befehle für arithmetische oder logische Verschiebungen.
Zyklische Verschiebung mit Übertragsbit ist besonders nützlich, wenn Verschiebungen mit Zahlen durchgeführt werden, die größer als die Wortbreite des Prozessors sind, weil die Zahl dann in zwei Registern gespeichert wird und das aus einem Register hinausgeschobene Bit in das andere Register hineingeschoben werden muss. Bei zyklischer Verschiebung mit Übertragsbit wird dieses Bit bei der ersten Verschiebung im Übertragsbit „gespeichert“ und bei der nächsten Verschiebung weitergegeben, ohne dass zusätzliche Instruktionen notwendig sind.
C und C++
In C, C++ und verwandten Sprachen werden die Verschiebungsoperatoren durch << und >> dargestellt. Die Anzahl der Verschiebungen wird als zweiter Operand übergeben. Beispiel:
x = y << 2;
weist der Variable x das Ergebnis der bitweisen Verschiebung von y um zwei Stellen nach links zu. Dies führt zum selben Ergebnis wie x = y * 4.
In C und C++ verwenden Berechnungen mit vorzeichenlosen Werten logische Verschiebungen; Berechnungen mit vorzeichenbehafteten Werten verhalten sich abhängig von der Implementierung (engl. implementation-defined behavior), sofern der rechte Operand negativ ist, durch einen Linksshift sich das Vorzeichen ändert oder ein negativer Wert einem Rechtsshift unterzogen wird.[1]
Ebenso ist das Ergebnis laut C- und C++-Sprachnorm undefiniert, wenn die Anzahl der Bitverschiebungen größer oder gleich der Bitbreite der Rechenarchitektur ist.[2] Wird beispielsweise auf einer 32-Bit-Architektur von Intel-Prozessoren gearbeitet (IA32), so bewirkt eine Verschiebung um 32 Stellen oft gar keine Veränderung des Ergebnisses, d. h. für x = y << 32 ergibt sich x == y. Der Grund liegt in der Art und Weise, wie die Compiler die Schiebeoperation in Maschinencode umsetzen. Die meisten Prozessoren haben direkte Befehle zum Schieben von Bits, wobei die Anzahl der Verschiebungen nur in begrenzter Breite im Maschinenbefehl codiert wird. Für IA32 sind z. B. 5 Bitstellen vorgesehen, um die Zahl der Verschiebungen abzulegen.[3] Daher können nur Verschiebungen im Bereich 0 bis 31 korrekt ausgeführt werden. Entsprechende Beschränkungen können für andere Architekturen und Datentypen ebenso vorhanden sein.
Java
In Java sind alle Ganzzahl-Datentypen vorzeichenbehaftet, und die Operatoren << und >> führen arithmetische Verschiebungen durch. In Java gibt es zusätzlich den Operator >>>, der eine logische Rechtsverschiebung durchführt. Da logische und arithmetische Linksverschiebungen identisch sind, gibt es keinen <<<-Operator.
ARM-Assembler
In ARM-Assembler werden die Verschiebungsoperatoren durch LSL(Logical Shift Left), LSR(Logical Shift Right) und ASR(Arithmetic Shift Right) dargestellt. Für die zyklischen Verschiebungen gibt es die beiden Befehle ROR(ROtate Right, ohne Übertragsbit) und RRX(Rotate Right eXtended, mit Übertragsbit).
Anwendungen
Obwohl Rechner oft effiziente Befehle zur Ausführung von arithmetischen und logischen Operationen eingebaut haben, können alle diese Operationen auch durch Kombinationen von bitweisen Operatoren und Nullvergleichen durchgeführt werden. Folgender Pseudocode zeigt beispielsweise, wie zwei beliebige Ganzzahlen a und b nur mithilfe von Verschiebungen und Additionen multipliziert werden können:
c := 0 solange b ≠ 0 falls (b und 1) ≠ 0 c := c + a schiebe a um 1 nach links schiebe b um 1 nach rechts return c
Der Code führt eine schriftliche Multiplikation im Binärsystem aus, allerdings in der unüblichen Reihenfolge von hinten nach vorne (beginnend mit der letzten Ziffer von b).
Siehe auch: Schriftliche Multiplikation im Binärsystem
Eine sehr interessante Anwendung des bitweisen XOR ist die Gewinnstrategie des Nim-Spiels, bei der die Anzahlen sowohl als Binärzahlen wie als Bitketten zu behandeln sind.
Weblinks
- Division durch bitweise Verschiebung (englisch)
Einzelnachweise
- ISO/IEC-Standard „C programming language“, Abschnitt 6.5.7#5 (englisch)
- A7.8 Shift Operators, Appendix A. Reference Manual, The C Programming Language
- SAL,SAR,SHL,SHR – Shift, Chapter 4. Instruction Set Reference, IA-32 Intel Architecture Software Developer’s Manual

