Außenwinkel

Die Außenwinkel eines konvexen Polygons sind die außen anliegenden Winkel zwischen einer Seite des Polygons und der Verlängerung einer benachbarten Seite. Jeder Außenwinkel ist der Nebenwinkel eines Innenwinkels und ergänzt diesen zu 180°. Die Summe der Außenwinkel eines Polygons ist unabhängig von der Anzahl seiner Ecken und ergibt stets 360°.

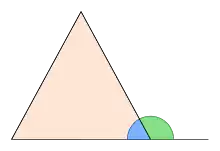
Innenwinkel (blau) und Außenwinkel (grün) eines Dreiecks

Nach dem Außenwinkelsatz ist in einem Dreieck jeder Außenwinkel gleich der Summe der beiden nichtanliegenden Innenwinkel. Die Winkelhalbierenden der Außenwinkel eines Dreiecks schneiden sich in den Ankreismittelpunkten.

Bezeichnungen

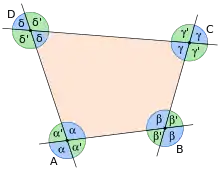
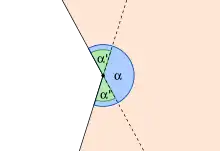
Bezeichnungen von Innen- und Außenwinkeln am Viereck ABCD

Werden die Seiten eines konvexen Polygons über die Ecken hinaus verlängert, entstehen vier Schnittwinkel, von denen je zwei gegenüberliegende kongruent sind. Derjenige Winkel, der im Inneren des Polygons liegt, heißt Innenwinkel des Polygons. Werden die Ecken des Polygons mit $A,B,C,\ldots$ bezeichnet, so werden die Innenwinkel meist $\alpha ,\beta ,\gamma ,\ldots$ genannt. Der dem Innenwinkel gegenüber liegende Scheitelwinkel ist gleich groß wie dieser und wird ebenso bezeichnet. Die beiden verbleibenden Winkel sind ebenfalls Scheitelwinkel und werden Außenwinkel des Polygons genannt. Die Außenwinkel werden üblicherweise mit $\alpha ',\beta ',\gamma ',\ldots$ bezeichnet (siehe Abbildung). Jeder Außenwinkel ist dabei der Nebenwinkel seines zugehörigen Innenwinkels, das heißt, es gilt

\alpha +\alpha '=\beta +\beta '=\gamma +\gamma '=\ldots =180^{\circ }

.

Sowohl die Innenwinkel als auch die Außenwinkel eines Polygons sind eindeutig den Ecken des Polygons zugeordnet. Den einem Außenwinkel zugehörigen Innenwinkel nennt man anliegenden Innenwinkel, während die übrigen Innenwinkel des Polygons nichtanliegende Innenwinkel genannt werden. Entsprechend wird ein Außenwinkel, der einem Innenwinkel zugeordnet ist, als anliegender Außenwinkel und die übrigen Außenwinkel des Polygons als nichtanliegende Außenwinkel bezeichnet.

Beispiele

Bei einem gleichseitigen Dreieck $\Delta ABC$ gilt für die Innen- und Außenwinkel

\alpha =\beta =\gamma =60^{\circ }~{\text{und}}~\alpha '=\beta '=\gamma '=120^{\circ }

.

Bei einem Rechteck $\Box ABCD$ gilt für die Innen- und Außenwinkel entsprechend

\alpha =\beta =\gamma =\delta =90^{\circ }~{\text{und}}~\alpha '=\beta '=\gamma '=\delta '=90^{\circ }

.

Bei einem gleichwinkligen Polygon, beispielsweise einem regelmäßigen Polygon, mit $n$ Ecken sind alle Außenwinkel gleich groß und messen jeweils $360^{\circ }/n$ .

Eigenschaften

Illustration des Außenwinkelsatzes

Außenwinkelsätze

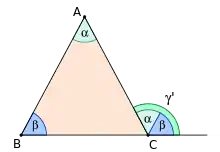
Der Außenwinkelsatz der euklidischen Geometrie besagt, dass der Außenwinkel eines Dreiecks stets gleich der Summe der beiden nichtanliegenden Innenwinkel ist. Es gilt demnach

\alpha '=\beta +\gamma ,~\beta '=\alpha +\gamma ~{\text{und}}~\gamma '=\alpha +\beta

(siehe die Abbildung für die dritte Gleichung). Der schwache Außenwinkelsatz besagt, dass der Außenwinkel eines Dreiecks stets strikt größer als jeder der beiden nichtanliegenden Innenwinkel ist, also

\alpha '>\beta ,~\alpha '>\gamma ,~\beta '>\alpha ,~\beta '>\gamma ,~\gamma '>\alpha ~{\text{und}}~\gamma '>\beta

.

Aus dem schwachen Außenwinkelsatz folgt auch, dass jeder Innenwinkel stets strikt kleiner als jeder der beiden nichtanliegenden Außenwinkel ist.

Winkelsumme

Die Innenwinkelsumme beträgt in einem konvexen Polygon mit $n$ Ecken

\alpha +\beta +\gamma +\ldots =(n-2)\cdot 180^{\circ }

.

Da anliegende Innen- und Außenwinkel sich jeweils zu 180° ergänzen, ergibt sich damit für die Außenwinkelsumme eines konvexen Polygons mit $n$ Ecken

\alpha '+\beta '+\gamma '+\ldots =(180^{\circ }-\alpha )+(180^{\circ }-\beta )+(180^{\circ }-\gamma )+\ldots =n\cdot 180^{\circ }-(n-2)\cdot 180^{\circ }=360^{\circ }

.

Die Summe der Außenwinkel eines konvexen Polygons beträgt demnach unabhängig von der Anzahl der Ecken stets 360°. Hierbei werden je zwei kongruente Außenwinkel nur einmal gezählt.

Winkelhalbierende

Dreieck mit Außenwinkelhalbierenden (grün), Innenwinkelhalbierenden (rot), Inkreis (blau) und Ankreisen (orange)

In den Ecken eines konvexen Polygons schneiden sich die Winkelhalbierenden der zugehörigen Außen- und Innenwinkel stets in einem rechten Winkel.

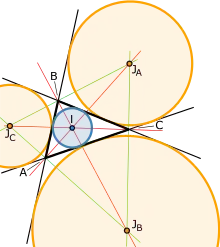
In einem Dreieck schneiden sich die Winkelhalbierenden der Außenwinkel verschiedener Ecken in den Ankreismittelpunkten $J_{A}$ , $J_{B}$ und $J_{C}$ des Dreiecks. Jeder dieser drei Schnittpunkte liegt zugleich auf der Winkelhalbierenden des jeweils nichtanliegenden Innenwinkels.

Weiterhin teilt die Außenwinkelhalbierende in einem Dreieck die verlängerte gegenüberliegende Seite des Dreiecks außen im Verhältnis der Längen der beiden dem Winkel anliegenden Seiten (siehe auch Kreis des Apollonios). Die Schnittpunkte der Außenwinkelhalbierenden mit den verlängerten gegenüberliegenden Seiten liegen dabei, sofern sie existieren, alle auf einer Geraden.

Verallgemeinerungen

Innen- und Außenwinkel an einer einspringenden Ecke

Nichtkonvexe Polygone

Innen- und Außenwinkel können auch bei nichtkonvexen Polygonen definiert werden. An einer einspringenden Ecke befinden sich die Außenwinkel allerdings dann im Inneren des Polygons. In einem solchen Fall wird dem Außenwinkel ein negatives Winkelmaß zugeordnet, sodass die Winkelsumme aus Außenwinkel und zugehörigem Innenwinkel weiterhin 180° beträgt. Auf diese Weise ergibt sich auch die Summe der Außenwinkel eines nichtkonvexen Polygons wie im konvexen Fall zu 360°.

Allgemeinere Geometrien

Der Begriff des Außenwinkels lässt sich auch in allgemeineren Geometrien, wie der absoluten Geometrie und der riemannschen Geometrie, definieren. Der schwache Außenwinkelsatz gilt auch in der absoluten Geometrie, während der Außenwinkelsatz in nichteuklidischen Geometrien nicht mehr richtig sein muss.

In der sphärischen Geometrie ist die Außenwinkelsumme eines Polygons stets kleiner als 360° während in der hyperbolischen Geometrie die Summe der Außenwinkel stets größer als 360° ist.

Literatur

Ilka Agricola, Thomas Friedrich: Elementargeometrie: Fachwissen Für Studium und Mathematikunterricht. Springer, 2010, ISBN 978-3-8348-9826-5, S. 15–18.
Susanne Müller-Philipp, Hans-Joachim Gorski: Leitfaden Geometrie: Für Studierende der Lehrämter. Springer, 2009, ISBN 978-3-8348-0097-8, S. 236–238.

Weblinks

Wiktionary: Außenwinkel – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Commons: Außenwinkel – Sammlung von Bildern, Videos und Audiodateien

Eric W. Weisstein: Exterior Angle. In: MathWorld (englisch).
Eric W. Weisstein: Exterior Angle Bisector. In: MathWorld (englisch).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.