Mittelparallele

Der Begriff Mittelparallele wird in der Geometrie in mehreren Bedeutungen verwendet.

Mittelparallele von zwei parallelen Geraden

Mittelparallele zweier Geraden

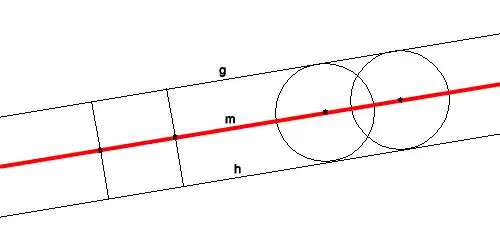
Sind zwei parallele Geraden g und h gegeben, so ist ihre Mittelparallele die Gerade, die von g und h jeweils den gleichen Abstand hat. Dies ist die am häufigsten benutzte Bedeutung.

Veranschaulichung: Der Mittelstreifen einer gerade verlaufenden Landstraße stellt im Prinzip eine Mittelparallele zwischen den Randstreifen der Straße dar.

Die Mittelparallele ist der geometrische Ort (die Menge) der Mittelpunkte aller Kreise, welche die gegebenen Geraden berühren, und der geometrische Ort aller Punkte, die von den beiden Geraden den gleichen Abstand haben, vergleiche Winkelhalbierende.

Mittelparallelen eines Dreiecks

Mittendreieck

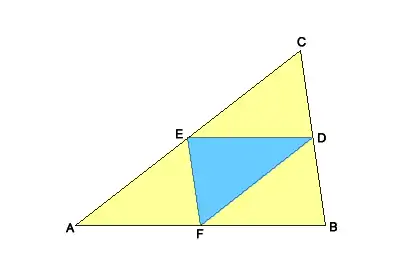
Die Verbindungsstrecken der Seitenmittelpunkte eines Dreiecks bezeichnet man als die Mittelparallelen (oder auch als Mittellinien) des Dreiecks, weil sie jeweils zu einer Seite des Dreiecks parallel sind. Jede dieser Mittelparallelen ist halb so lang wie die zugehörige Seite des Dreiecks. (Satz von der Mittelparallelen im Dreieck)

{\overline {ED}}={\frac {1}{2}}{\overline {AB}};\qquad {\overline {FE}}={\frac {1}{2}}{\overline {BC}};\qquad {\overline {DF}}={\frac {1}{2}}{\overline {CA}}

Die drei Mittelparallelen eines Dreiecks bilden das so genannte Mittendreieck. Es ist zum ursprünglichen Dreieck ähnlich.

Mittelparallele eines Trapezes

Mittelparallele in einem Trapez

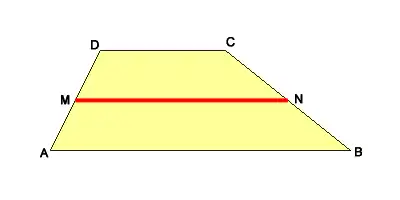
Die Mittelparallele eines Trapezes ist die Verbindungsstrecke der Mittelpunkte der beiden nicht notwendig parallelen Seiten. Diese Strecke ist parallel zu den beiden parallelen Seiten (Grundseiten) des Trapezes.

Die Länge der Mittelparallelen ergibt sich als arithmetisches Mittel der Längen der beiden Grundseiten:

{\overline {MN}}={\frac {1}{2}}({\overline {AB}}+{\overline {DC}})

Mit Hilfe der Mittelparallele des Trapezes lässt sich auch die Trapezfläche berechnen. Dazu multipliziert man die Länge der Mittelparallelen mit der Höhe des Trapezes, d. h. dem Abstand der beiden parallelen Grundseiten.

Literatur

Hans Schupp: Elementargeometrie. Schöningh, Hannover 1977, ISBN 3-506-99189-2.
I. N. Bronstein, K. A. Semendjajev, G. Musiol, H. Mühlig (Hrsg.): Taschenbuch der Mathematik. 7., vollständig überarbeitete und ergänzte Auflage. Verlag Harri Deutsch, Frankfurt am Main 2008, ISBN 978-3-8171-2007-9.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.