Tangentenviereck
Ein Tangentenviereck ist ein Viereck, dessen Seiten Tangenten eines Kreises sind. Diesen Kreis nennt man den Inkreis des Tangentenvierecks. Ein solches Tangentenviereck ist immer konvex. Vierecke, bei denen lediglich die verlängerten Seiten Tangenten eines Kreises sind und die damit auch nicht notwendigerweise konvex sein müssen, sind keine Tangentenvierecke im Sinne der hiesigen Definition. Spezielle Tangentenvierecke sind das Quadrat, die Raute und das Drachenviereck.
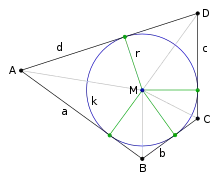
Eigenschaften
Für jedes Tangentenviereck gilt der Satz von Pitot: Die Summe der Längen zweier gegenüberliegender Seiten ist gleich der Summe der Längen der anderen beiden Seiten. Es gilt also
Umgekehrt gilt auch, dass jedes konvexe Viereck mit einen Inkreis besitzt und somit ein Tangentenviereck ist. Der Satz von Pitot und seine Umkehrung werden zusammen auch als Satz vom Tangentenviereck bezeichnet.
Der Mittelpunkt des Inkreises ist der Schnittpunkt der Winkelhalbierenden aller vier Innenwinkel. Deshalb müssen sich beim Tangentenviereck alle Winkelhalbierenden auch in einem Punkt schneiden.
Außerdem ist ein Viereck, das kein Trapez ist, genau dann ein Tangentenviereck, wenn eine der folgenden Bedingungen gilt:
Dabei ist E der Schnittpunkt der Geraden und und F ist der Schnittpunkt der Geraden und .
Sind P, Q, R, S die Fußpunkte der Lote des Inkreismittelpunkts M auf die Seiten AB, BC, CD, DA und der Inkreisradius des Tangentenvierecks, dann sind die rechtwinkligen Dreiecke MSA und APM nach dem Kongruenzsatz SWS kongruent, weil sie die Seite AM gemeinsam haben und außerdem und gilt. Daraus folgt, dass die Innenwinkel dieser rechtwinkligen Dreiecke jeweils gleich sind, also gilt auch . Entsprechend gilt , und . Die Summe dieser acht Teilwinkel am Inkreismittelpunkt M ist gleich 360°. Daraus folgt schließlich und , also . Die Summe der gegenüber liegenden Winkel am Inkreismittelpunkt beträgt also jeweils 180°.[1]
Formeln
| Mathematische Formeln zum Tangentenviereck | ||
|---|---|---|
| Flächeninhalt | 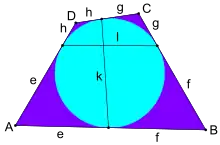 | |
| Umfang | ||
| Länge der Diagonalen | ||
| Inkreisradius | ||
Ein interessanter Spezialfall liegt vor, wenn ein Tangentenviereck die Bedingung
erfüllt. Unter dieser Voraussetzung ist das Tangentenviereck zugleich ein Sehnenviereck, also ein Viereck mit Inkreis und Umkreis. Die Formel für den Flächeninhalt von Sehnenvierecken liefert in diesem Fall das einfache Ergebnis
Mithilfe des Satz des Pythagoras und des Kosinussatz erhält man die Längen der tangentialen Sehnen und . Es gilt
Daraus ergibt sich das Längenverhältnis[1]
Siehe auch
Literatur
- Hartmut Wellstein, Peter Kirsche: Elementargeometrie. Springer, 2009, ISBN 978-3-8348-0856-1, S. 60-61
- Siegfried Krauter, Christine Bescherer: Erlebnis Elementargeometrie: Ein Arbeitsbuch zum selbstständigen und aktiven Entdecken. Springer, 2012, ISBN 978-3-8274-3025-0, S. 77-78
- Lorenz Halbeisen, Norbert Hungerbühler, Juan Läuchli: Mit harmonischen Verhältnissen zu Kegelschnitten: Perlen der klassischen Geometrie. Springer 2016, ISBN 978-3-662-53034-4, S. 21; Auszug (PDF; 4,1 MB)
Weblinks
- Eric W. Weisstein: Tangential Quadrilateral. In: MathWorld (englisch).
Einzelnachweise
- Martin Josefsson: Calculations concerning the tangent lengths and tangency chords of a tangential quadrilateral, Forum Geometricorum
- Nicusor Minculete: Characterizations of a Tangential Quadrilateral, Forum Geometricorum