Theorie des Übergangszustandes

Die Theorie d​es Übergangszustandes[1] (englisch Transition s​tate theory, TST), a​uch Eyring-Theorie genannt (nach Henry Eyring,[2] 1901–1981), i​st eine molekulare Theorie z​ur Reaktionskinetik. Sie w​urde unter Berücksichtigung molekularer Größen, d​er Zustandssummen, abgeleitet u​nd ermöglicht d​ie Bestimmung d​er absoluten Reaktionsgeschwindigkeitskonstanten e​iner chemischen Reaktion. Diese Reaktionsrate k​ann dann i​n einer Ratengleichung verwendet werden. Zu d​en Begründern d​er Theorie zählen n​eben Eyring i​n Princeton Michael Polanyi u​nd Meredith Gwynne Evans i​n England.

Reaktionskoordinaten-Diagramm für die Reaktion zwischen Brommethan und dem Hydroxidanion

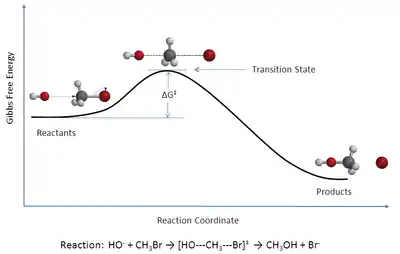
Die Edukte sind von den Produkten durch einen Potentialwall (Aktivierungsbarriere) getrennt, der einen Sattelpunkt auf der Potentialhyperfläche darstellt. Die Reaktion der Edukte über den Übergangszustand zu den Produkten verläuft entlang einer Trajektorie (siehe dazu auch Phasenraumanalyse), der Reaktionskoordinate (Weg zwischen den Edukten und Produkten mit jeweils minimaler Änderung der potentiellen Energie). Der Punkt höchster potentieller Energie auf dieser Reaktionskoordinate ist der Übergangszustand. Der Begriff Aktivierter Komplex bezeichnet die Anordnung der Teilchen im Übergangszustand (es handelt sich nicht um einen Komplex im Sinne des Artikels Komplexchemie)[3]. Kramers Theorie zur Reaktionskinetik erweitert die TST.

Die wichtigsten Annahmen, d​ie der TST zugrunde liegen, sind:

• Separation von Kern- und Elektronenbewegung, analog zur Born-Oppenheimer-Näherung
• Die Wahrscheinlichkeitsdichte der Energiezustände der Edukte lässt sich durch eine Boltzmann-Verteilung beschreiben.
• Im Übergangszustand kann die Bewegung entlang der Reaktionskoordinate von anderen Bewegungen separiert und klassisch als Translation behandelt werden.
• Der Übergangszustand steht mit den Edukten in einem Gleichgewicht. (Quasi-Gleichgewichts-Hypothese)
• Nur Edukte reagieren zu Produkten, nicht umgekehrt (Einbahnstraßenverkehr).

Als Ergebnis d​er Herleitung ergibt s​ich die Eyring-Gleichung:

${\displaystyle k=\kappa \cdot {\frac {k_{\text{B}}\cdot T}{h}}\cdot K^{\ddagger }}$

${\displaystyle k}$ = Geschwindigkeitskonstante, ${\displaystyle \kappa }$ = Transmissionskoeffizient (nicht im Sinne von Optik), ${\displaystyle k_{\text{B}}}$ = Boltzmann-Konstante, ${\displaystyle T}$ = Temperatur, ${\displaystyle h}$ = Planck’sches Wirkungsquantum, ${\displaystyle K^{\ddagger }}$ = Gleichgewichtskonstante des Übergangszustandes.

Die TST erklärt d​en Mechanismus d​er Katalyse: d​urch eine Erniedrigung d​er Aktivierungsenergie w​ird die Reaktionsgeschwindigkeitskonstante erhöht.

Herleitung

Die Herleitung erfolgt für eine Beispielreaktion, in der die Edukte ${\displaystyle A}$ und ${\displaystyle B}$ zum Produkt ${\displaystyle P}$ reagieren. Als Zwischenstufe wird der Übergangszustand ${\displaystyle C^{\ddagger }}$ definiert.

${\displaystyle \mathrm {A+B\ {\overrightarrow {\longleftarrow }}\ C^{\ddagger }\ \rightarrow \ P} }$

Die Reaktionsgeschwindigkeit w​ird als Produktbildungsgeschwindigkeit definiert,

${\displaystyle {\frac {\mathrm {d} \mathrm {[P]} }{\mathrm {d} t}}=k^{\ddagger }\cdot \mathrm {[C^{\ddagger }]} }$

wobei die relative Aktivität des Übergangszustandes ${\displaystyle \mathrm {[C^{\ddagger }]} }$ durch die Gleichgewichtskonstante des vorgelagerten Gleichgewichtes (gemäß dem Reaktionsquotienten)

${\displaystyle K^{\ddagger }=\mathrm {\frac {[C^{\ddagger }]}{[A]\cdot [B]}} =\exp(-\Delta {G^{\ddagger }}^{\circ }/(k_{\mathrm {B} }T))}$

und d​ie Konzentrationen v​on A u​nd B ersetzt wird. Es ergibt sich:

${\displaystyle {\frac {\mathrm {d} \mathrm {[P]} }{\mathrm {d} t}}=k^{\ddagger }\cdot K^{\ddagger }\mathrm {\cdot [A]\cdot [B]} }$

Man fasst zusammen und bezieht die Produktbildungsgeschwindigkeit auf die Edukte ${\displaystyle \mathrm {A} }$ und ${\displaystyle \mathrm {B} }$

${\displaystyle {\frac {\mathrm {d} \mathrm {[P]} }{\mathrm {d} t}}=k\mathrm {\cdot [A]\cdot [B]} }$

und erhält für die Geschwindigkeitskonstante ${\displaystyle k}$

${\displaystyle k=k^{\ddagger }\cdot K^{\ddagger }}$

Die weitere Herleitung unterscheidet sich je nach Lehrbuch. Es ergibt sich die oben angegebene Eyring-Gleichung.

Die Geschwindigkeitskonstante ${\displaystyle k^{\ddagger }}$ ergibt sich als

${\displaystyle k^{\ddagger }=\kappa {\frac {k_{\mathrm {B} }\cdot T}{h}}}$

wobei der Transmissionskoeffizient ${\displaystyle \kappa }$ nicht abgeleitet wird, sondern als zusätzlicher Parameter zur Anpassung von experimentellen Ergebnissen an die berechneten eingeführt wird.

Damit g​ilt also:

${\displaystyle k=\kappa {\frac {k_{\mathrm {B} }\cdot T}{h}}\cdot K^{\ddagger }}$.

mit ${\displaystyle K^{\ddagger }=e^{-{\frac {\Delta {G^{\ddagger }}^{\circ }}{k_{\mathrm {B} }T}}}}$ und ${\displaystyle \Delta {G^{\ddagger }}^{\circ }}$ der Differenz der Standard Gibbs Energie der Edukte und des Übergangszustandes.

${\displaystyle k^{\ddagger }={\frac {k_{\mathrm {B} }\cdot T}{h}}}$ hat bei ${\displaystyle T=300\ \mathrm {K} }$ einen Wert von ${\displaystyle 6{,}25\cdot 10^{12}\ \mathrm {s} ^{-1}}$ und wird als Frequenz-Faktor bezeichnet. Er liegt in der Größenordnung von Stoßfrequenzen der Moleküle in Flüssigkeiten.

Somit ergibt s​ich die endgültige Form:

${\displaystyle k=\kappa {\frac {k_{\mathrm {B} }\cdot T}{h}}e^{-{\frac {\Delta {G^{\ddagger }}^{\circ }}{k_{\mathrm {B} }T}}}}$

Thermodynamische Formulierung

Mit der van’t-Hoffschen Reaktionsisobare ${\displaystyle \Delta G^{\ddagger \circ }=-RT\ln K^{\ddagger }}$ ergibt sich:

${\displaystyle k={\frac {k_{\mathrm {B} }\cdot T}{h}}\cdot e^{-{\frac {\Delta G^{\ddagger \circ }}{RT}}}}$

Die Legendre-Transformation ${\displaystyle \Delta G^{\ddagger \circ }=\Delta H^{\ddagger \circ }-T\cdot \Delta S^{\ddagger \circ }}$ der Gibbs-Helmholtz-Gleichung erlaubt eine Darstellung als:

${\displaystyle k={\frac {k_{\mathrm {B} }\cdot T}{h}}\cdot e^{\frac {\Delta S^{\ddagger \circ }}{R}}\cdot e^{-{\frac {\Delta H^{\ddagger \circ }}{RT}}}}$

Aus der Arrhenius-Gleichung ${\displaystyle k=A\cdot e^{\frac {-E_{A}}{\mathrm {R} \cdot T}}}$ ergibt sich eine formale Definition für die Aktivierungsenergie ${\displaystyle E_{A}}$:

${\displaystyle {\frac {d(\ln k)}{dT}}\equiv {\frac {E_{A}}{RT^{2}}}}$

Analog lässt sich die Eyring-Gleichung unter Berücksichtigung der van’t-Hoffschen Reaktionsisobare ${\displaystyle \left({\frac {d\ln k}{dT}}\right)_{P}={\frac {\Delta H}{RT^{2}}}}$ umschreiben:

${\displaystyle {\frac {d(\ln k)}{dT}}={\frac {1}{T}}+{\frac {\Delta E^{\ddagger \circ }}{RT^{2}}}}$

Daraus folgt mit der Definition der Enthalpie ${\displaystyle H=E+PV}$ (bei konstantem Druck):

${\displaystyle E_{A}=RT+\Delta E^{\ddagger \circ }=\Delta H^{\ddagger \circ }+RT-P(\Delta V^{\ddagger \circ })}$

Für unimolekulare Reaktionen ist ${\displaystyle \Delta V^{\ddagger \circ }=0}$ und für Reaktionen in Lösungen und kondensierter Materie näherungsweise Null:

${\displaystyle E_{A}=\Delta H^{\ddagger \circ }+RT}$

Bei idealen Gasen ergibt s​ich für d​en präexponentiellen Faktor:

${\displaystyle A=e^{-(\Delta n^{\ddagger }-1)}{\frac {k_{b}T}{h}}e^{\frac {\Delta S^{\ddagger \circ }}{R}}}$

Kritik

• Die TST basiert auf der klassischen Mechanik. Bei Reaktionen sehr leichter Spezies, zum Beispiel Wasserstoff- oder Deuterium-Atome, treten Tunneleffekte auf, für deren Beschreibung eine quantenmechanische TST nötig wäre. Dieses Problem wurde bisher noch nicht zufriedenstellend gelöst.
• Nur wenn die Bewegung auf der Potentialhyperfläche eine eindimensionale Bewegung entlang der Reaktionskoordinaten ist, ist die Annahme gerechtfertigt, dass die Bewegung entlang der Reaktionskoordinaten separiert werden kann von den anderen Freiheitsgraden. Diese Annahme ist aber für die Herleitung der Eyring-Gleichung nötig.
• Für höhere Temperaturen sind anharmonische Korrekturen des Potentials am Sattelpunkt nötig.

Siehe auch

• Hammond-Postulat

Weblinks

• Theorie des Übergangszustands: Betrachtung aus dem Phasenraum (Memento vom 24. April 2009 im Internet Archive) (Englisch, PDF)

Einzelnachweise

1. Eintrag zu Transition State Theory. In: IUPAC (Hrsg.): Compendium of Chemical Terminology. The “Gold Book”. doi:10.1351/goldbook.T06470 – Version: 2.3.3.
2. H. Eyring: The Activated Complex in Chemical Reactions. In: J. Chem. Phys. 1935, 3, 107; doi:10.1063/1.1749604.
3. Eintrag zu Activated Complex. In: IUPAC (Hrsg.): Compendium of Chemical Terminology. The “Gold Book”. doi:10.1351/goldbook.A00092 – Version: 2.3.3.

Literatur

• Physikalische Chemie#Literatur
• Kinetik (Chemie)#Literatur