Hauptebene (Optik)

Hauptebenen sind zwei beim Arbeitsmodell Paraxiale Optik in einem Abbildungssystem definierte Ebenen, in denen vereinfacht die Brechungen der Lichtstrahlen angenommen werden.[1] Im Raum zwischen den Hauptebenen werden die Lichtstrahlen parallel zur optischen Achse verlaufend gedacht. Vorteil der Hauptebenen ist, dass ein Mehrlinsensystem, z. B. ein Objektiv, durch nur eine dünne Linse mit nur einer äquivalenten Brennweite und zwei Hauptebenen ausgedrückt werden kann. Die Berechnung der Hauptebenen kann allgemein mittels der Matrizenoptik erfolgen.

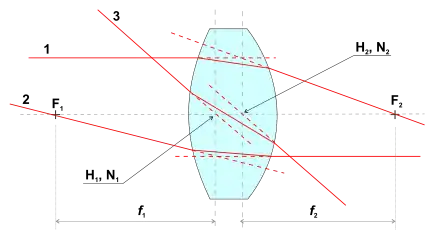
Abbildung 1: Hauptebenen und Hauptpunkte in einer relativ dicken Linse: Im Arbeitsmodell Paraxiale Optik werden die Strahlen an den Grenzflächen ungebrochen (gestrichelt) bis zur jeweiligen Hauptebene weiter geführt und erst dort gebrochen (Mittenstrahl 3 nur parallel versetzt) dargestellt.

Die Hauptebenen sind die Bezugsebenen für Entfernungsmessungen, die eine im Objektraum, die andere im Bildraum. Entsprechende Entfernungen sind die Brennweite und die Objekt- und die Bildweite, die in der Linsengleichung auf einfache Weise (lineare Gleichung der Kehrwerte) miteinander verknüpft sind.

Eine dünne Linse und ein schwach gekrümmter sphärischer Spiegel erfüllen weitestgehend die Voraussetzungen für Paraxiale Optik und Anwendung der Linsengleichung. Als für deren abbildende Eigenschaft nötige Bezugsebenen können bereits die Tangentialebenen an die Scheitelpunkte der Oberflächen angenommen werden. Da die beiden Oberflächen bei einer dünnen Linse fast zusammenfallen, spricht man hier von nur einer in der Mitte angenommenen Hauptebene.

Bei der Arbeit mit der Linsengleichung bleiben mit Ausnahme der chromatischen Aberration alle anderen Abbildungsfehler unberücksichtigt. Diese treten umso stärker auf, je größer die Winkel zwischen Strahlen und optischer Achse sind. Deshalb ist das Konzept Paraxiale Optik, in das die Hauptebenen gehören, auf kompakte optische Systeme nur ausdehnbar, wenn die Linsenfehler unter Zuhilfenahme entsprechend aufwändigerer Arbeitsmodelle korrigiert sind. Diese Interpretation der Paraxialen Optik bezeichnet man als Gaußsche Optik.

Die Schnittpunkte der Hauptebenen mit der optischen Achse sind die Hauptpunkte, die mit H (objektseitiger) und H' (bildseitiger Hauptpunkt) bezeichnet werden (in nebenstehender Abbildung H₁ und H₂).

Bei komplexen Abbildungssystemen kann die bildseitige Hauptebene auch „vor“ der objektseitigen liegen. Ein afokales Linsensystem hat keine Hauptebenen, bzw. liegen diese im Unendlichen.

Hauptebenen-Konstruktion für eine Linse

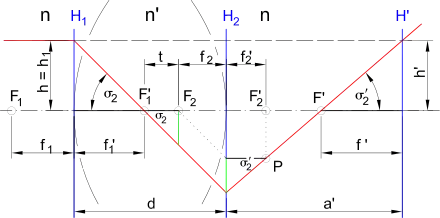
Abbildung 2: Konstruktion des bildseitigen Brennpunkts F' und der bildseitigen Hauptebene H'
Linse besteht aus den brechenden Flächen H₁ und H₂

Der Brennpunkt F' ist die Abbildung des Brennpunkts F'₁ der Fläche H₁ durch die Fläche H₂.[2] Ein in die Linse einfallender achsparalleler Strahl (rot in nebenstehender Abbildung) passiert den bildseitigen Brennpunkt F'.
Das Konzept der Hauptebenen bedeutet, dass zwischen ihnen der Abbildungsmaßstab 1 beträgt. Ein Punkt in H₁ hat in H' den gleichen Abstand von der optischen Achse: h' = h.

Die Hauptebene H' enthält den Schnittpunkt des achsparallel einfallenden und von der Linse in den Brennpunkt F' abgelenkten Strahls (rot) mit dem unabgelenkt verlängerten achsparallel einfallenden Strahl (unterbrochene Linie in nebenstehender Abbildung).

a'={\overline {H_{2}H'}}={\frac {f'_{2}d}{d-f'_{1}-f_{2}}}

.[3]

Analoges gilt auf der Objektseite:

{\overline {H_{1}H}}={\frac {f_{1}d}{d-f'_{1}-f_{2}}}

.

Wenn die Linse relativ dünn ist ( $d\ll f_{1},f_{2}$ ; bei der dünnen Linse ist definitionsgemäß $d=0$ ), werden diese Abstände zu Null. Die Hauptebenen verbleiben auf den Scheiteln der Flächen, die in einer Ebene $H$ zusammen fallen.

Hauptebenen-Konstruktion für ein System aus zwei dünnen Linsen

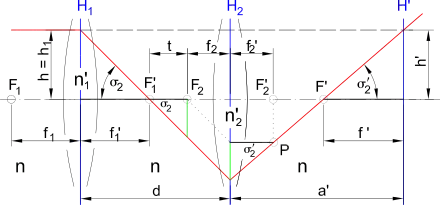
Abbildung 3: System aus zwei dünnen Linsen (H₁ und H₂)
Konstruktion des bildseitigen Brennpunkts F' und der bildseitigen Hauptebene H'

Die Konstruktion ist analog zu der für eine Linse (siehe oben). Zu beachten ist lediglich, dass die Hauptebenen H₁ und H₂ je zwei brechende Flächen repräsentieren und dass zu jeder zwei gleich große Brennweiten (objekt- und bildseitig) gehören. Möglich ist auch, dass die beiden dünnen Linsen aus verschiedenem Material bestehen (n'₁≠n'₂).

Die beiden oben stehenden Gleichungen ändern sich geringfügig (aber mit prinzipiell anderen Ausdrücken für die Brennweiten $f$ ) zu:

a'={\overline {H_{2}H'}}={\frac {f_{2}d}{d-f_{1}-f_{2}}}

,

{\overline {H_{1}H}}={\frac {f_{1}d}{d-f_{1}-f_{2}}}

.

Beim Zusammenrücken der dünnen Linsen ( $d<<f_{1},f_{2}$ ) gehen die Abstände auch gegen Null. Die Hauptebene H₁ oder H₂ oder eine anstelle von beiden angenommene Ebene H repräsentiert das System aus zum Beispiel zwei zusammengekitteten dünnen Linsen.

Durch Kombination der mit Hilfe der Abbildungen 2 und 3 beschriebenen einzelnen Konstruktionen findet man die Hauptebenen-Konstruktion für ein System aus zwei Linsen mit deutlicher Dicke (“dicke Linse”).

Anmerkungen und Einzelnachweise

Das nächst genauere und aufwändigere Arbeitsmodell ist die Geometrische Optik
Heinz Haferkorn: Optik: Physikalisch-technische Grundlagen und Anwendungen, Barth, 1994, ISBN 3-335-00363-2, S. 198 und 207.
Heinz Haferkorn: Optik: Physikalisch-technische Grundlagen und Anwendungen, Barth, 1994, ISBN 3-335-00363-2, S. 200. Im Unterschied zu Haferkorn werden die Brennweiten hier ohne Vorzeichen geschrieben.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Das nächst genauere und aufwändigere Arbeitsmodell ist die Geometrische Optik

[2] Heinz Haferkorn: Optik: Physikalisch-technische Grundlagen und Anwendungen, Barth, 1994, ISBN 3-335-00363-2, S. 198 und 207.

[3] Heinz Haferkorn: Optik: Physikalisch-technische Grundlagen und Anwendungen, Barth, 1994, ISBN 3-335-00363-2, S. 200. Im Unterschied zu Haferkorn werden die Brennweiten hier ohne Vorzeichen geschrieben.