Numerische Apertur

Die numerische Apertur (Formelzeichen $A_{\text{N}}$ , NA oder n.A.; abgeleitet von numerisch und Apertur, etwa: Zahlenwert der Öffnungsweite) ist eine dimensionslose Größe bei optischen Systemen wie Teleskopen, Lichtmikroskopen oder Lichtwellenleitern. Der Zahlenwert hängt ab vom Öffnungswinkel (auch: Akzeptanzwinkel) des optischen Systems und vom Brechungsindex des umgebenden Mediums. Je größer Brechungsindex und Öffnungswinkel sind, desto größer ist auch die numerische Apertur. Dadurch steigt sowohl die Menge an Licht, die aufgenommen wird, als auch das erzielbare Auflösungsvermögen. Durch eine erhöhte Auflösung ist einerseits eine Darstellung von kleineren Objektdetails in Bildern, die mit dem System erzeugt wurden, möglich, andererseits kann ein System wie zum Beispiel ein Mikroskop mit höherer Auflösung genutzt werden um Licht auf einen kleineren Fokuspunkt zu konzentrieren.

Mikroskopobjektiv mit eingravierten Werten für die Vergrößerung (10x) und die numerische Apertur (0,25).

Die numerische Apertur ist wesentlich vom vordersten optischen Element eines Systems abhängig, beispielsweise bei Mikroskopen von der Frontlinse des Objektivs. Auf guten Mikroskopobjektiven ist der Wert daher eingraviert.

Der Begriff numerische Apertur wurde vom Physiker Ernst Abbe eingeführt, der an Lichtmikroskopen arbeitete.[1]

Mathematische Beschreibung und Beispiele

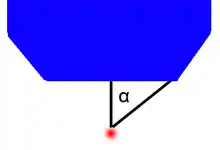
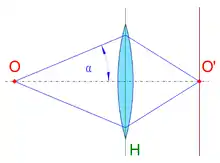
Der halbe Öffnungswinkel α eines Objektivs. Hier beträgt der Wert etwa α = 50°. Für ein Trockenobjektiv (ohne Immersion) ergibt das eine numerische Apertur von sin 50° = 0,77. Der rote Punkt stellt das scharf gestellte Objekt dar.

Der halbe objektseitige Öffnungswinkel α für die Bestimmung der numerischen Apertur bei der optischen Abbildung eines Objektpunktes O nach O' mit Brechung der Randstrahlen an der Hauptebene H einer Feldlinse

Der (objektseitige) Öffnungswinkel (auch: Akzeptanzwinkel) eines optischen Systems oder Objektivs entspricht dem maximal möglichen Winkel eines Lichtbündels, das vom scharf gestellten Objekt ausgeht und vom Objektiv gerade noch aufgenommen wird. Der Öffnungswinkel gibt also an, wie groß der maximale Lichtkegel ist, der vom Objekt ausgehend vom Objektiv aufgenommen wird. Die numerische Apertur $A_{\text{N}}$ berechnet sich aus dem Sinus des halben Öffnungswinkels ( $\alpha$ multipliziert mit dem Brechungsindex n des Materials zwischen Objektiv und Präparat (siehe auch Immersion (Mikroskopie))):

A_{\text{N}}=n\cdot \sin \alpha

Befindet sich zwischen Objektiv und Präparat Vakuum oder Luft beträgt der Brechungsindex $n=1$ oder fast genau 1. Ein Objektiv, welches alles Licht für die Abbildung verwenden würde, das von vorne kommt, hätte theoretisch einen Öffnungswinkel von 180°, der halbe Öffnungswinkel hätte 90° und der Sinus hiervon wäre 1. Die numerische Apertur wäre demnach auch 1. Ein solches Objektiv ist jedoch technisch nicht realisierbar, der Öffnungswinkel ist immer deutlich kleiner als 180°.

Mikroskopobjektive, die in Luft arbeiten (also ohne Immersion), haben deshalb immer eine numerische Apertur kleiner 1. Bei sehr guten Exemplaren kann der Wert bis zu 0,95 betragen. 0,95 ist der Sinus von 72°, der Öffnungswinkel eines solchen Objektivs liegt demnach bei 144°. Da ein Fernrohr in Luft arbeitet ist auch hier die numerische Apertur immer kleiner als eins.

Bei Lichtmikroskopen kann die numerische Apertur Werte größer als eins annehmen, wenn der Raum zwischen zu mikroskopierendem Präparat und Mikroskop-Objektiv mit einer Immersionsflüssigkeit gefüllt wird. Deren Brechungsindex ist größer als eins. Häufig wird Wasser ( $n=1{,}33$ ), Glycerin ( $n=1{,}47$ ) oder spezielles Immersionsöl ( $n=1{,}51$ ) benutzt. Hierfür sind jedoch spezielle Objektive erforderlich, die für diese Mittel berechnet sind.

Bei Mikroskopen steigt die numerische Apertur häufig mit der Vergrößerungszahl des Objektivs. Die stark vergrößernden Objektive (meist 60x, 63x oder 100x, aber auch bei hochauflösenden Varianten von 20x und 40x-Objektiven) brauchen dementsprechend Immersionsflüssigkeit zwischen Objektiv und Präparat (Deckglas). Bei einem Öffnungswinkel von 140° ergibt sich für ein Trockenobjektiv eine numerische Apertur von 0,94 aber für Wasserimmersionsobjektive eine von 1,25 und für Ölimmersionsobjektive eine von 1,43.[2] Entsprechend höher ist die Lichtstärke und das Auflösungsvermögen der Immersionsobjektive.

Besonders hohe numerische Aperturen von 1,45–1,47 weisen Ölobjektive auf, die für interne Totalreflexionsfluoreszenzmikroskopie (TIRF) bestimmt sind.

Zusammenhang mit dem Auflösungsvermögen

Je kleiner ein Objekt ist, desto stärker ist der Effekt der Beugung von Lichtwellen an diesem Objekt. „Stärker“ bedeutet hier, dass das gebeugte Licht in einem größeren seitlichen Winkel vom Objekt abgelenkt wird. Von diesem zur Seite gebeugten Licht muss mindestens ein Teil aufgefangen werden, um das Objekt im erzeugten Bild auflösen zu können. Objektive mit größerem Öffnungswinkel nehmen daher nicht nur hellere Bilder auf, sie erzielen auch eine bessere Auflösung.

Die erzielbare Auflösung eines Mikroskops in der Schärfeebene hängt jedoch nicht linear vom Öffnungswinkel ab, sondern linear von der numerischen Apertur. Beispielsweise ergibt sich bei Hellfeldmikroskopie und gerader Beleuchtung von unten (ohne Kondensor) ein minimaler Abstand $d_{\text{min}}$ , den zwei Strukturen mindestens haben müssen um getrennt wahrgenommen werden zu können, von

d_{\text{min}}={\frac {\lambda }{A_{\text{N}}}}

wobei ${\lambda }$ die Wellenlänge des verwendeten Lichts ist. Bei größeren Werten für ${A_{\text{N}}}$ wird der minimale Abstand $d_{\text{min}}$ also kleiner, die Auflösung verbessert sich.

Die optische Auflösung spielt nicht nur eine Rolle bei der Erzeugung von Bildern, sondern auch wenn Licht auf einen möglichst kleinen Punkt fokussiert werden soll, etwa bei der Herstellung von integrierten Schaltkreisen. Auch hier ist durch Beugung begrenzt, wie klein der erzeugte Lichtfleck werden kann. Eine höhere numerische Apertur erlaubt die Fokussierung des Anregungslichts in einen kleineren Lichtfleck. Auf Grund der Beugung ist der erzeugte Lichtfleck jedoch kein Punkt, sondern ein Beugungsscheibchen beziehungsweise im dreidimensionalen Raum eine Punktspreizfunktion.

Praktische Zusammenhänge

Auch bei Lichtwellenleitern wird die numerische Apertur beschrieben durch den Sinus des Akzeptanzwinkels (manchmal auch Kollimations-/Divergenzwinkel) der Faser. Sie entspricht der Öffnung des kegelförmigen Lichtbündels, das aus der Endfläche der Faser austritt (siehe auch Abschnitt Multimodefaser im Artikel Lichtwellenleiter).

Bei optischen Abbildungen sind bei manchen optischen Systemen die Abbildungsfehler so groß, dass das über die numerische Apertur berechenbare theoretisch mögliche Auflösungsvermögen nicht erreicht wird. Als Kompromiss wird in der Fotografie häufig die kritische Blende eingestellt, bei der bei einem vorgegebenen Objektiv in der Praxis das größte Auflösungsvermögen erreicht werden kann. In der Fotografie wird anstelle der numerischen Apertur häufig das Öffnungsverhältnis angegeben. Dieses bezieht sich – anders als die numerische Apertur – auf den bildseitigen Öffnungswinkel (siehe Öffnungsverhältnis und Blendenzahl).

Literatur

Ernst Abbe: Die Lehre von der Bildentstehung im Mikroskop. bearbeitet von Otto Lummer und Fritz Reiche, Verlag Vieweg, 1910.
Rainer Danz: Numerische Apertur, Immersion und förderliche Vergrößerung (PDF; 16 MB). In: Innovation. 15, Carl Zeiss AG, 2005, S. 12–16.

Weblinks

Wikibooks: Numerische Apertur – Lern- und Lehrmaterialien

Mikroskop. In: Physikalisches Praktikum. Technische Universität Dresden (PDF-Datei; 415 kB)

Einzelnachweise

Eugene Hecht: Optik. 4. Auflage, Verlag Oldenbourg, 2005, ISBN 3-486-27359-0, Kapitel 5.7 Optische Systeme, S. 357.
Ernst Leitz: Anleitung zum Gebrauche der Mikroskope. Hrsg.: Optische Werkstätte von Ernst Leitz Wetzlar. S. 13 (Nachdruck von Leica Mikroskopie und Systeme GmbH, D-6330 Wetzlar 1).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Eugene Hecht: Optik. 4. Auflage, Verlag Oldenbourg, 2005, ISBN 3-486-27359-0, Kapitel 5.7 Optische Systeme, S. 357.

[2] Ernst Leitz: Anleitung zum Gebrauche der Mikroskope. Hrsg.: Optische Werkstätte von Ernst Leitz Wetzlar. S. 13 (Nachdruck von Leica Mikroskopie und Systeme GmbH, D-6330 Wetzlar 1).