Atmosphärische Gezeiten

Atmosphärische Gezeitenwellen mit Perioden von einem ganzen und einem halben solaren Tag (meridionale Wellenzahlen m = 1 und 2) sowie Wellen mit Perioden von einem ganzen und einem halben Jahr (meridionale Wellenzahl m = 0) sind großskalige atmosphärische Wellen mit horizontalen Dimensionen von der Größenordnung des Erdumfangs. Der Vollständigkeit halber kann man auch noch das zonale klimatische Mittel dazurechnen.

Einführung

Die Erdatmosphäre ist ein riesiger Wellenleiter mit einem festen Untergrund (die Erdoberfläche) und nach oben hin offen. In einem solchen Wellenleiter kann eine beliebige Zahl von Eigenmoden existieren. Die Atmosphäre ist jedoch ein nichtlineares chaotisches System, sodass nur großskalige Wellen mit kleinen Amplituden aus dem meteorologischen Rauschen herausgefiltert werden können. Die kleinerskaligen Wellen tragen zum meteorologischen Rauschen bei. Großskalige atmosphärische planetare Wellen existieren für alle Perioden von wenigen Stunden bis zu Jahren.[1] Aus diesem breiten Spektrum ragen deutlich die ganztägige Gezeitenwelle sowie die Jahreswelle heraus.

Gezeitenwellen sowie Jahres- und Halbjahreswellen werden durch die differentielle solare Erwärmung in der Atmosphäre erzeugt. Sie heißen deshalb thermische Gezeiten. Die gravitativ bedingte Gezeitenkraft des Mondes, die bekanntlich für die Ozeangezeiten von fundamentaler Bedeutung ist, kann ebenfalls lunare atmosphärische Gezeiten erzwingen, die jedoch viel schwächer als die thermischen Gezeiten sind. Gravitativ erzwungene solare Gezeiten sind so klein, dass sie nicht von den solaren thermischen Gezeiten getrennt werden können.

Solare Wärmequelle

Ein Teil der sichtbaren Sonnenstrahlung wird direkt in der unteren Atmosphäre, vorzugsweise in den Wolken, absorbiert (etwa 24 %). Dieser Teil ist eine wesentliche Quelle für die Erzeugung der thermischen Gezeiten. Ein etwas größerer Teil (46 %) dringt bis zur Erdoberfläche vor und erhitzt den Untergrund.[2] Sowohl Wolken als auch Erdoberfläche reflektieren etwa 30 % in den Weltraum zurück (Albedo). Die Ozeanoberfläche wird vor allen Dingen in niedrigen Breiten stark erhitzt, und das Oberflächenwasser verdampft. Feuchte Luft dringt nach oben. Bei der Bildung von Wolken gibt die mit Wasserdampf gesättigte Luft latente Wärme an die Umgebung ab. Auf Grund dynamischer Prozesse verteilt sich diese latente Wärme bis in die mittleren Breiten und modifiziert dadurch die durch die direkt absorbierte Sonnenstrahlung erzeugte Wärme.

Im Höhenbereich zwischen etwa 20 und 60 km wird ein breites Band von solarer Ultraviolett-Strahlung absorbiert (Ozonschicht). Dies stellt eine zweite Wärmequelle für die Gezeitenwellen dar.[3] Röntgen- und Extrem-Ultraviolett-Strahlen werden oberhalb etwa 85 km (der Thermosphäre) fast vollständig absorbiert und bilden damit eine dritte Wärmequelle zur Erzeugung von Gezeitenwellen. Schließlich gibt es eine vierte Wärmequelle in den Polarlichtzonen der Thermosphäre. Ein magnetosphärisches elektrisches Konvektionsfeld treibt elektrische Ströme im Höhenbereich um 100–150 km (ionosphärische Dynamoschicht). Ohmsche Verluste dieser Ströme erhitzen das thermosphärische Gas in diesen Breiten.

Die thermische Effektivität der einzelnen Atmosphärenschichten wächst mit der Höhe. Während sie in der unteren Atmosphäre von der Größenordnung 0,01 bis 0,1 W/kg ist, beträgt diese in der Thermosphäre 1 bis 10 W/kg. Diese Differenz hat zur Folge, dass Gezeiten in der Troposphäre nur ein marginales Phänomen, in der Thermosphäre dagegen ein dominierendes Ereignis sind[4].

Gezeitentheorie

Wellengleichung

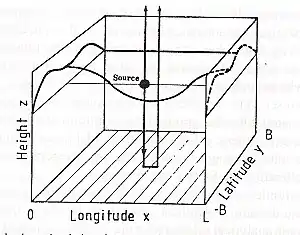
Abbildung 1.: Rechteckige Box, die den atmosphärischen Wellenleiter simulieren soll. Sie besitzt einen festen Boden (den Erdboden) und ist nach oben offen. Die Abszisse x ersetzt die geographische Länge λ, die Ordinate y ersetzt die geographische Breite φ. Eine Punktquelle erzeugt aufwärts und abwärts laufende Wellenmoden. Die abwärts laufende Welle wird am Erdboden reflektiert, sodass oberhalb der Quelle nur noch aufwärts laufende Wellen existieren können (Ausstrahlungsbedingung). Die eingezeichnete Meridionalstruktur einer Wellen ist die der ganztägigen Gezeitenwelle (1, -2, -1).

Für einen rechteckigen Wellenleiter der Form von Abb. 1 ist die Lösung der Wellengleichung (z. B. für den Vertikalwind w):

(1)\qquad w=w_{0}[e^{ik_{z}}-e^{-ik_{z}}]\cos(k_{y})e^{i(k_{x}-\omega t)}

mit (x, y, z) den kartesischen Koordinaten, t der Zeit, ω der Kreisfrequenz, k_x = 2πm/L, k_y = π(n-1/2)/B konstanten horizontalen Wellenzahlen, (n, m) ganzen Zahlen und (L, 2B) den Dimensionen der Box. Die vertikale Wellenzahl wird dann bestimmt aus der Dispersionsgleichung

(2)\qquad k_{z}={\sqrt {\omega ^{2}/c^{2}-k_{x}^{2}-k_{y}^{2}}}

mit c der Lichtgeschwindigkeit. Gl. (1) beschreibt die Ausbreitung von zwei freien charakteristischen nach oben und nach unten laufenden Wellen, die oberhalb ihres Quellengebietes sich nur nach oben ausbreiten können (Ausstrahlungsbedingung).

Eine ähnliche Gleichung lässt sich für ultralange Wellen in einer isothermen sphärischen Hintergrund-Atmosphäre mit konstanter Skalenhöhe H entwickeln (Laplace-Gleichung). Dazu ist eine strikte Linearisierung der hydrodynamischen und thermodynamische Gleichungen notwendig, und die Wellenamplituden müssen klein gegenüber den Parametern (Dichte, Druck, Temperatur) der Hintergrund-Atmosphäre sein. Dies gilt für die Gezeitenwellen sowohl in der Troposphäre als auch in der Thermosphäre. Im Höhenbereich zwischen etwa 50 und 100 km können ihre Amplituden so groß werden, dass nichtlineare Effekte, insbesondere Turbulenz, die Wellenstruktur zerstören kann.

Durch die Linearisierung ist eine Separation der Variablen in die Horizontalstrukturen geographische Breite und Länge (φ, λ) sowie Höhe z möglich. Die nach oben laufende Welle der der Gl. 1 äquivalenten Lösung ist dann[5][6]

(3)\qquad w=w_{0}e^{(1-ik_{z})\zeta }\Theta _{n}^{m}(\phi ,\nu )e^{i(m\lambda -\omega t)}

Hier ist die Längenabhängigkeit die Gleiche wie in Gl. 1 (x = a λ; mit a dem Erdradius). Die Meridionalstruktur wird jetzt durch die Hough-Funktion Θ_n^m(φ, ν) ersetzt, die nicht nur von der zonalen Wellenzahl n, sondern auch von der meridionalen Wellenzahl m und der normierten Frequenz ν = ω/Ω (mit Ω = 7,29 × 10⁻⁵ s⁻¹ der siderischen Kreisfrequenz der Erdrotation) abhängig ist. Weiterhin ist ζ = z/(2H) eine normierte Höhe. Die Hough-Funktion ist die Lösung der Laplace-Gleichung. Sie kann nur numerisch bestimmt werden und lässt sich durch eine Summe von Kugelfunktionen approximieren. In der Thermosphäre entwickeln sich diese Eigenmoden zu den Kugelfunktionen selbst. Wie in Gl. 1 ist die zonale Wellenzahl n ein Maß für die Zahl der Nullstellen innerhalb eines Erdquadranten. Die vertikale Wellenzahl k_z wird nun

(4)\qquad k_{z}={\sqrt {\epsilon _{n}^{m}/\epsilon _{c}-1}}

mit ε_n^m einem Eigenwert (Lamb-Parameter) und ε_c = (aΩ)²/(κgH) ≈ 9,5 einer Konstanten. H ≈ 8 km ist die mittlere Skalenhöhe, g = 9,81 m/s² die Gravitationsbeschleunigung und κ = 1 - c_v/_p = 0,29 (mit c_v, c_p den spezifischen Wärmen des Atmosphärengases bei konstantem Volumen bzw. konstantem Druck). Bemerkenswert ist die exponentielle Zunahme der Wellen mit der Höhe in Gl. 3 gemäß exp{z/(2H)}. Solange die Wellen sich ohne Verluste nach oben in ein Gebiet exponentiell abnehmender Dichte ausbreiten, müssen ihre Amplituden aus Energieerhaltungsgründen exponentiell wachsen. Die Folgen dieses Wachstums machen sich vor allen Dingen in der mittleren Atmosphäre bemerkbar, wo die Amplituden solche Größen erreichen können, dass die Bedingungen der Linearisierung nicht mehr erfüllt sind. Die Wellen werden turbulent und geben ihre Wellenenergie an das sie umgebende Gas ab. Weiter bemerkenswert für die atmosphärische Wellenausbreitung im Allgemeinen ist, dass die vertikalen Komponenten der Phasen- und Gruppengeschwindigkeit entgegengesetzt laufen. Eine aufwärtsgehende Welle besitzt eine Phasengeschwindigkeit, die nach unten gerichtet ist.

Aus Gl. 4 erkennt man, dass die vertikale Wellenzahl k_z imaginär wird, wenn ε_n^m < ε_c ist. Wellen mit reellen Werten von k_z heißen interne Wellen. Sie besitzen endlich große vertikale Wellenlängen und können Wellenenergie nach oben transportieren. Ihre Amplituden wachsen exponentiell mit der Höhe. Wellen mit imaginären vertikalen Wellenzahlen heißen externe Wellen. Sie besitzen unendlich große vertikale Wellenlängen, und ihre Wellenenergie nimmt, falls ik_z > 1 ist, außerhalb ihres Quellengebietes exponentiell ab. Sie können keine Wellenenergie transportieren.[6] Atmosphärische Schwerewellen und die meisten der atmosphärischen Gezeiten, die in der unteren Atmosphäre angeregt werden, gehören zu den internen Wellen. Da ihre Amplituden exponentiell wachsen, werden diese Wellen spätestens im Höhenbereich um 100 km durch Turbulenz zerstört. Alle jahreszeitlichen Wellen (m = 0) sind externe Wellen.

Lösung der Laplace-Gleichung

Michael Longuet-Higgins[7] hat die Laplace-Gleichung vollständig gelöst. Er hat entdeckt, dass es auch negative Eigenwerte ε_n^m gibt. Es gibt zwei Klassen von Wellenmoden: Wellen der Klasse I, die mit positiven Indices n gekennzeichnet werden, und Wellen der Klasse II mit negativen n. Die Klasse II-Wellen existieren nur auf Grund der Corioliskraft und verschwinden für Perioden kleiner als 12 h (|ν| > 2). Wellen mit geraden n sind symmetrisch in Bezug auf den Äquator, Wellen mit ungeraden n sind antisymmetrisch. Die Wellen werden gekennzeichnet durch das Zahlentripel (m, n, ν).

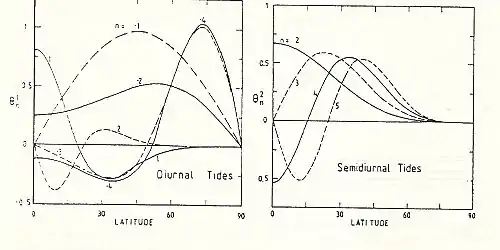
Abbildung 2. Meridionalstruktur der Druckamplituden der Hough-Funktionen der ganztägigen Wellen (m = 1; ν = -1) (links) und der halbtägigen Wellen (m = 2; ν = -2) (rechts) auf der Nordhemisphäre. Ausgezogene Linien: symmetrische Wellen; gestrichelte Linien: antisymmetrische Wellen

Die fundamentale ganztägige Gezeitenwelle (1, -2, -1) ist eine externe Welle. Sie wandert mit der Sonne nach Westen. Sie besitzt den Eigenwert von ε_-2¹ = - 12.56. Die wichtigste halbtägige Welle (2, 2, -2) ist eine interne Welle mit ε₂¹ = 12.21. Abb. 2 zeigt die Meridionalstrukturen der Druckamplituden der Hough-Funktionen der wichtigsten ganztägigen (m = 1; links) und halbtägigen Wellen (m = 2; rechts). Die von ihrer Meridionalstruktur her am besten an die Wärmequelle in der Troposphäre angepasste ganztägige Gezeitenwelle (1,-2,1) spielt als externe Welle in der unteren Atmosphäre nur eine marginale Rolle. In der Thermosphäre entwickelt sich diese Welle jedoch zur dominanten Gezeitenwelle. Sie treibt den elektrischen Sq-Strom im Höhenbereich zwischen etwa 100 und 200 km (ionosphärische Dynamoschicht).

Verlustprozesse

Für eine Linearisierung der hydro- und thermodynamischen Gleichungen führt man eine Parametrisierung der Reibungs- und Wärmeverluste ein. Die turbulente Reibung wird durch einen Rayleigh-Reibungsterm ν_R, proportional zum negativen Horizontalwind U, die turbulente Wärmeleitung durch einen Newton-Kühlungsterm ν_N, proportional zur negativen Temperatur, ersetzt. Beide Terme sind reine empirische Zahlen, die aus den Beobachtungen abgeleitet werden müssen. Die Verlustprozesse erscheinen nun in den komplexen (normierten) Frequenzen ν_r = ν + iν_R und ν_h = ν + ν_N, sodass die vertikale Wellenzahl k_z komplex wird:

(5)\qquad k_{z}={\sqrt {\epsilon _{n}^{m}\nu _{r}/(\epsilon _{c}\nu _{h})-1}}

Das Verhältnis ν_R/ν_N heißt Prandtl-Zahl. Die Terme ν_R und ν_N besitzen in der Troposphäre Größenordnungen von ca. 0,1 (oder reziproke Werte von 1/ν_R ≈ 10 Tagen), und sind deshalb für Gezeiten mit Perioden von 24 h und kleiner unbedeutend. In der Thermosphäre erreichen sie jedoch auf Grund der Kollision des Neutralgases mit dem ionosphärischen Plasma Werte von ca. 1 und größer (oder reziproke Werte von 1/ν_R < 1 Tag).[8] Das bedeutet, dass alle Gezeitenwellen oberhalb etwa 150 km externe Wellen werden, und dass ihre Hough-Funktionen graduell zu Kugelfunktionen degenerieren. Aus dem Mode (1, -2, -1) wird die Kugelfunktion P₁¹(φ), Mode (2, 2, -2) entwickelt sich zu P₂²(φ) usw., mit φ der geographischen Breite.[6] In der Thermosphäre ist der ganztägige Mode (1, -2, -1) die dominierende Gezeitenwelle mit Temperaturamplituden von ca. 15 % der global gemittelten Exosphären-Temperatur (ca. 1000–1500 K) und Horizontalwinden der Größenordnung von 100 m/s (siehe Abb. 4).[9]

Vertikalstruktur

Auf Grund der Linearisierung der hydro- und thermodynamischen Gleichungen ist die Separation in Horizontalstruktur und Vertikalstruktur möglich. Die Laplace-Gleichung liefert die Horizontalstruktur in Form von Houghschen Wellenmoden. Der Eigenwert ε_n^m in Gl. 4 verbindet die Horizontalstruktur mit den nur noch von der Höhe z abhängigen Gleichungen der Vertikalstruktur. Besonders einfache Lösungen existieren für eine isotherme Atmosphäre (Skalenhöhe H = const.). Die Lösung besteht aus einer partikulären Lösung, die direkt proportional zur Wärmequelle ist, sowie einer freien nach oben laufenden Welle mit der vertikalen Wellenzahl k_z in Gl. 4. Die obere Randbedingung ist die Ausstrahlungsbedingung: Oberhalb der Wärmequelle dürfen nur noch nach oben laufende Wellen existieren.

Beobachtungen

Wandernde Wellen

Die beiden wichtigsten solaren thermischen Gezeitenwellen sind die nach Westen mit der Sonne wandernden ganztägigen und halbtägigen Gezeitenwellen. Ihre über ein Jahr gemittelten Druckamplituden am Erdboden haben die Gestalt (in Pa)[10][5]

S_{1}=59\cos ^{3}\phi \cos[\tau _{S}-5,2h]

S_{2}=116\cos ^{3}\phi \cos[2(\tau _{S}-9,7h)]

mit τ_S = Ω_S t + λ der Lokalzeit, Ω_S der Kreisfrequenz eines solaren Tages, (φ, λ) geographische Breite und Länge und t der Universalzeit. Beide Quellen sind symmetrisch in Bezug auf den Äquator. Die Welle S₁ besteht aus dem fundamentalen externen Mode (1, -2, -1) und dem nächsthöheren internen Mode (1, 2, -1) (siehe Abb. 2). Die Welle S₂ entspricht im Wesentlichen dem internen Mode (2, 2, -2). Die Amplitude der ganztägigen Welle ist um den Faktor 2 kleiner als die der halbtägigen Welle, obgleich die spektrale Amplitude ihrer Wärmequelle um den Faktor 2 größer ist. Die externe Welle wird also um den Faktor 4 gegenüber der internen Welle unterdrückt.

Nicht wandernde Wellen

Es handelt sich um großskalige stehende Wellen mit der Periode von einem Tag oder einem Jahr und Oberwellen. Sie sind abhängig von der Universalzeit und werden durch orographisch bedingte Differenzen der Erdoberfläche (Kontinent-Ozean-Kontrast, Topographieunterschiede, klimatologische Unterschiede etc.) erzeugt. Eine wichtige Quelle dieser Wellen ist die Konvektion in den Tropen.

Von besonderer Bedeutung ist die stehende antisymmetrische Gezeitenwelle der Wellenzahl m = 1 und der Periode von einem Jahr. Sie wird erzeugt durch Druckunterschiede entlang eines Breitengrades. Im Winter existiert ein Hochdruckgebiet über dem nördlichen Atlantik und ein Tiefdruckgebiet über Sibirien mit Temperaturunterschieden von etwa 50 °C. Im Sommer ist es umgekehrt. Eine solche Welle lässt sich durch die Rossby-Haurwitz-Welle Θ_-3¹ (für Rossby-Haurwitz-Wellen gilt ε = 0[6]) beschreiben. Ihr zonaler Wind hat angenähert die Breitenstruktur der Kugelfunktion P₂¹ = 3 sin φ cos φ.

Aus den Eulerschen Gleichungen der Kreiselbewegungen lässt sich mit Hilfe einer solchen Anregungsfunktion die jahreszeitliche Komponente der Polbewegung des geographischen Pols gegenüber der Rotationsachse des Erdkörpers bestimmen. Die Druckamplitude der Anregungsfunktion ist von der Größe 1,2 hPa. Der gleiche Wellentyp mit der Periode von ca. 430 bis 440 siderischen Tagen ist für das Chandler-Wobbeln in der Umgebung der Chandler-Resonanz-Periode von 441 siderischen Tagen verantwortlich.[11]

Lunare Gezeitenwellen

Die stärkste lunare Gezeitenwelle besitzt die Druckamplitude an der Erdoberfläche (in Pa) von

L_{2}=6\cos ^{3}\phi \cos[2\tau _{L}-15^{o}]

mit τ_L der lunaren Ortszeit. Diese Amplitude ist an der Erdoberfläche um den Faktor 20 kleiner als die der solaren halbtägigen Welle. Es ist schwierig, sie aus dem meteorologischen Rauschen herauszufiltern.[5] Auch hier gibt es noch kleinere Oberwellen.

Untere Atmosphäre

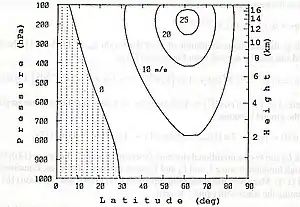
Abbildung 3.: klimatisches Mittel des zonalen Windes als Funktion der Höhe und der Breite; die Ostwindzone in Äquatornähe ist punktiert.

Das klimatische Mittel des zonalen Windes (m = ν = 0) innerhalb der Troposphäre zeigt in mittleren und höheren Breiten im Wesentlichen Westwinde (von Westen nach Osten gerichtet), die mit der Höhe zunehmen und in etwa 30° bis 45° Breite mit zwei Strahlströmen in 12 bis 15 km Höhe mit Stärken von der Größenordnung 20 bis 30 m/s kulminieren (siehe Abb. 3). Während der Solstizien wird der Strahlstrom in der Sommerhemisphäre um etwa 10 m/s verstärkt und in der Winterhemisphäre entsprechend abgeschwächt. In niedrigen Breiten überlagert sich ein Ostwind (die Passatwinde), der ein Maximum am Erdboden von ungefähr 5 m/s besitzt und in etwa 15 km (der Tropopause) verschwunden ist.[12]

Der solare Wärmeüberschuss in niedrigen Breiten erzeugt einen Temperaturabfall vom Äquator zu den Polen. In einer idealen Atmosphäre ohne Verlustprozesse würde die Corioliskraft einen zonalen Westwind (geostrophischer Wind) auf beiden Hemisphären erzeugen, und der Wärmetransport würde schließlich durch Wärmeleitung erfolgen. Die reale Atmosphäre ist jedoch instabil, und den Wärme- und Druckausgleich innerhalb der Westwinddrift besorgen Turbulenzzellen aller Größenordnungen von Hoch- und Tiefdruckgebieten bis hin zur Kleinturbulenz. Der Wärmetransport von niedrigen zu hohen Breiten ist außerordentlich komplex (barokline Instabilität).[13][14] In unserer Annäherung ist dies pauschal durch die Verlustterme Rayleigh-Reibung ν_R und Newton-Kühlung ν_N berücksichtigt. Für das tägliche synoptische Wettergeschehen sind die relativ zur Westwärtsdrift nach Westen wandernden Rossby-Haurwitz-Wellen vorzugsweise der meridionalen Wellenzahlen m = 4 - 7 beteiligt. Im klimatischen Mittel sind sie bereits herausgemittelt.

Der fundamentale Wellenmode (0, -2, iν_R) ist ein externer Mode und besitzt die zonale Windkomponente

u_{-2}^{0}(\phi ,z)=a_{1}(z)P_{1}^{1}(\phi )+a_{3}(z)P_{3}^{1}(\phi )+...

Die Kugelfunktion P₁¹ = cos φ beschreibt die starre Superrotation (oder retrograde Rotation) der Atmosphärenschicht in der Höhe z. An der Erdoberfläche findet aber eine Reibung zwischen Atmosphärengas und Erde statt. Der Westwind des Wellenmodes (0,-2, iν_R) sorgt deshalb für eine Beschleunigung der Erdrotation. Die Reaktionszeit beträgt etwa 7 Tage, so dass der Erdkörper auf kleinerperiodische Vorgänge nicht reagiert. Nun besagt aber ein Fundamentalgesetz der Physik, dass der Drehimpuls eines Systems konstant bleibt, solange keine externen Drehmomente wirksam sind. Im klimatischen Mittel darf demnach die Erde durch die Atmosphäre nicht beschleunigt (oder abgebremst) werden, und es muss im Mittel der starre Rotationsterm der Atmosphäre an der Erdoberfläche verschwinden, so dass Atmosphäre und Erdkörper im klimatischen Mittel abgekoppelt sind. Das bedeutet aber, dass zum Wellenmode (0, -2, iν_R) noch ein Ostwind-Term u_S = - a_S cos φ hinzugefügt werden muss, der diese Entkopplung erzwingt (a₁ + a_S = 0 an der Erdoberfläche z = 0) und für den Passatwind verantwortlich ist. Der Wellenmode, der die starre Superrotation der Atmosphäre beschreibt, ist eine Rossby-Haurwitz-Welle der meridionalen Wellenzahl m = 0.[11]

Es lässt sich ein einfaches Modell des zonalen Windes mit lediglich dem Wellenmode (0, -2, iν_R) sowie einer Rossby-Haurwitz-Welle konstruieren, wobei als untere Randbedingung das Verschwinden der Superrotationskomponente des zonalen Windes sowie eine plausible Wärmequelle mit einem Maximum in 5 km Höhe angenommen werden.[11] Das Ergebnis (Abb. 3) zeigt bereits die Grundstruktur der Beobachtungen. Die Lage des Strahlstroms in 60° anstatt 45° Breite ist bedingt durch das einfache Modell und lässt sich leicht mit weiteren Wellenmoden korrigieren. Der zonale Wind in der Nähe der Erdoberfläche entspricht in erster Näherung der Kugelfunktion

P_{3}^{1}(\phi )=1.5\cos(\phi )(5\sin ^{2}(\phi )-1)

Sie beschreibt einen Westwind in mittleren Breiten und einen Ostwind in niedrigen Breiten. Die Nullstelle dieser Kugelfunktion ist bei φ = ± 27°. Im klimatischen Mittel gibt die Atmosphäre in mittleren und hohen Breiten Drehimpuls an den Erdkörper ab, der in niedrigen Breiten vom Erdkörper wieder der Atmosphäre hinzugefügt wird. Das gilt auch für alle anderen Windkomponenten mit n >1. Über die Sphäre gemittelt verschwindet deren Drehimpulsübertragung.

Dieses Modell ist bewusst vereinfacht und setzt eine homogene Erdoberfläche voraus, um die wesentlichen Prozesse darzustellen. Die reale Oberflächenstruktur der Erde wird das Bild sicherlich modifizieren.

Erhaltung des Drehimpulses

Wegen der Drehimpulserhaltung muss sich eine vorübergehende Änderung des atmosphärischen Drehimpulses in einer entsprechenden Änderung des Drehimpulses des Erdkörpers bemerkbar machen. Dies wird in der Tat bei den ganz- und halbjährlichen Amplituden des zonalen Windes beobachtet, die mit entsprechenden Schwankungen der Tageslänge korreliert sind.[15][16] Die periodische Änderung der Amplitude einer äquivalenten starren Rotation der Atmosphäre (d. h. der gesamten Atmosphäre) von Δa₁ ≃ 0,9 m/s entspricht einer Änderung der Tageslänge von Δτ ≃ 34 Millisekunden, mit einem Maximum am 3. Februar. Entsprechende Zahlen für die halbjährige Periode sind Δa₁ ≃ 0,8 m/s und 0,29 Millisekunden mit Maxima am 8. Mai und 8. November.[17] Es gibt außerdem Fluktuationen von 10 Tagen von der Größe von 0,1 Millisekunden, ebenso wie Fluktuationen, die das El-Niño-Phänomen im Passatwind über dem Stillen Ozean widerspiegeln.[18][19]

Mittlere Atmosphäre

Die dominierende Welle in der mittleren Atmosphäre ist die ganzjährige Welle (0, -1, iν_R) (ν << ν_R). Während der Äquinoktien bilden sich zwei Strahlströme aus: ein Westwind-Strahlstrom auf der Winterhemisphäre und ein Ostwind-Strahlstrom auf der Sommerhemisphäre von je 70 m/s in etwa 65 bis 70 km Höhe und 50° bis 60° Breite. Das klimatische Mittel und die halbjährliche Welle sind dagegen relativ klein und von der Größenordnung von 20 m/s.[12] Die Wärmequelle für diese Strahlströme ist die absorbierte solare Ultraviolett-Strahlung, die auch die Ozonschicht erzeugt.

Gezeiten in der Thermosphäre

Oberhalb etwa 150 km Höhe degenerieren alle atmosphärischen Wellen zu externen Wellen, und es ist kaum mehr eine vertikale Wellenstruktur sichtbar. Ihre Meridionalstruktur ist die der Kugelfunktionen P_n^m mit n einer zonalen Wellenzahl und m der meridionalen Wellenzahl (m = 0: zonal gemittelte Wellen; m = 1: ganztägige Wellen; m = 2: halbtägige Wellen etc.). Die Thermosphäre verhält sich in erster Näherung wie ein gedämpftes Oszillatorsystem mit Tiefpassfilterwirkung. Das heißt, dass kleinskalige Wellen (mit großen Wellenzahlen n und m) gegenüber den großskaligen Wellen unterdrückt werden. Im Falle geringer magnetosphärischer Aktivität kann man die beobachtete zeitlich und örtlich variierende Exosphärentemperatur durch eine Summe von Kugelfunktionen beschreiben:[20]

(6)\qquad T(\phi ,\lambda ,t)=T_{oo}[1+\Delta T_{2}^{0}P_{2}^{0}(\phi )+\Delta T_{1}^{0}P_{1}^{0}(\phi )\cos[\omega _{a}(t-t_{a}]+\Delta T_{1}^{1}P_{1}^{1}(\phi )\cos(\tau -\tau _{d})+...]

Abbildung 4. Schematischer Meridional-Höhen-Querschnitt der Zirkulationssysteme von (a) symmetrischer Windkomponente des zonalen Mittels (P₂⁰), von (b) antisymmetrischer Windkomponente (P₁⁰), und (d) symmetrischer ganztägigen Windkomponente (P₁¹) um 3 h und 15 h Lokalzeit. (c) zeigt die horizontalen Windvektoren der ganztägigen Welle auf der Nordhemisphäre

Es ist φ die geographische Breite, λ die geographische Länge, t die Zeit, ω_a die Kreisfrequenz der Jahrsperiode, τ = ω_dt + λ die Lokalzeit und ω_d die Kreisfrequenz eines solaren Tages. t_a = 21. Juni ist die Zeit des Sommeranfangs auf der Nordhemisphäre und τ_d = 15:00 die Lokalzeit des Temperaturmaximums.

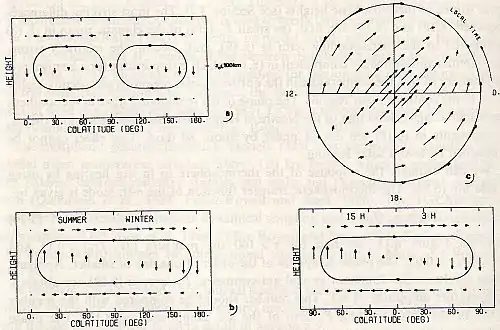
Der erste Term rechts in Gl. 6 ist die global gemittelte Temperatur der Exosphäre (von der Größenordnung von T_∞ ≈ 1000 K). Der zweite Term [(mit P₂⁰ = 0,5(3 sin²φ - 1)] wird durch die unterschiedliche solare Erwärmung in niedrigen und hohen Breiten erzeugt. Ein thermisches Windsystem entsteht mit Winden hin zu den Polen im oberen Zirkulationsast und entgegengesetzten Winden im unteren Ast (Abb. 4a). Es sorgt für einen Wärmeausgleich zwischen niedrigen und hohen Breiten. Der Koeffizient ΔT₂⁰ ≈ 0,004 ist klein, da die joulesche Erwärmung in den Polarlichtzonen den solaren XUV-bedingten Wärmeüberschuss in niedrigen Breiten teilweise kompensiert. Der dritte Term (mit P₁⁰ = sin φ) ist für den Transport des Wärmeüberschusses auf der Sommerhemisphäre in die Winterhemisphäre verantwortlich. Seine relative Amplitude ist etwa ΔT₁⁰ ≃ 0,13. Der vierte Term schließlich (mit P₁¹ = cos φ der dominierenden Gezeitenwelle (1, -2, -1)) beschreibt den Transport des Wärmeüberschusses von der Tagseite auf die Nachtseite (Abb. 4d). Seine relative Amplitude ist etwa ΔT₁¹ ≃ 0,15. Weitere Terme (z. B. halbjährige, halbtägige Wellen etc.) müssen zur Gl. 10 hinzuaddiert werden. Sie sind jedoch von geringerer Bedeutung. Entsprechende Summen lassen für Luftdruck, Luftdichte, Gaskonstituenten etc. herleiten.[21]

Einzelnachweise

N. K. Vinnichenko: The kinetic energy spectrum in the free atmosphere: 1 second to 5 years. In: Tellus. 22, 1970, S. 158.
F. Möller: Einführung in die Meteorologie. Bibliographisches Institut, Mannheim 1973.
J. M. Forbes: Atmospheric tides I + II. In: J. Geophys. Res. 87, 1980, S. 5222, 5241.
R. S. Stolarski, P. B. Hays, R. G. Roble: Atmospheric Heating by Solar EUV Radiation. In: Journal of Geophysical Research. Band 80, Nr. 16, 1975, S. 2266–2276, doi:10.1029/JA080i016p02266.
S. Chapman, R.S. Lindzen: Atmospheric Tides. D. Reidel, Dordrecht 1970.
H. Volland: Atmospheric Tidal and Planetary Waves. Kluwer Publ., Dordrecht 1988.
M. S. Longuet-Higgins: The eigenfunctions of Laplace's equations over a sphere. In: Phil. Trans. Roy. Soc. London, A262, 1968, S. 511.
J. R. Holton, W.M. Wehrbein: A numerical model of the zonal mean circulation of the middle atmosphere. In: Pageoph. 118, 1980, S. 284.
H. Kohl, J. W. King In: J. Atm. Terr. Phys. 29, 1967, S. 1045.
Manfred Siebert: Atmospheric Tides. In: Advances in Geophysics. Volume 7. Elsevier, 1961, ISSN 0065-2687, S. 105–187.
H. Volland: Atmosphere and earth's rotation. In: Surv. Geophys. 17, 1996, S. 1001.
R. J. Murgatroyd: The structure and dynamics of the stratosphäre. In: G. A. Coby (Hrsg.): The Global Circulation of the Atmosphere. In: Roy. Met. Soc. London, 1969, S. 159.
H. Fortak: Meteorologie. Deutsche Buchgemeinschaft, Berlin 1971.
J. R. Holton: An Introduction to Dynamic Meteorology. Academic Press, New York 1992.
D. S. Robertson: Geophysical applications of Very-Long-Baseline Interferometry. In: Rev. Modern Phys. 14, 1993, S. 1.
T. M. Eubanks, J.A. Steppe, J.O. Dickey, P.S. Challahan: A spectral analysis of earths angular momentum budget. In: J. Geophys. Res. 90, 1985, S. 53787.
R. D. Rosen: The axial momentum balance of earth and its fluid envelop. In: Surv. Geophys. 14, 1993, S. 1.
W. E. Carter, D.S. Robinson: Studying the earth by very-long-baseline interferometry. In: Sci. American. 44, 1986, S. 225.
R. Hide, J. O. Dickey: Earth's variable rotation. In: Sciences. 235, 1991, S. 629.
W. Köhnlein: A model of thermospheric temperature and composition. In: Planetary and Space Science. Band 28, Nr. 3, März 1980, S. 225–243, doi:10.1016/0032-0633(80)90015-X.
U. von Zahn, W. Köhnlein, K. H. Fricke, U. Laux, H. Trinks, H. Volland: Esro 4 model of global thermospheric composition and temperatures during times of low solar activity. In: Geophysical Research Letters. Band 4, Nr. 1, 1977, S. 33–36, doi:10.1029/GL004i001p00033.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] N. K. Vinnichenko: The kinetic energy spectrum in the free atmosphere: 1 second to 5 years. In: Tellus. 22, 1970, S. 158.

[2] F. Möller: Einführung in die Meteorologie. Bibliographisches Institut, Mannheim 1973.

[3] J. M. Forbes: Atmospheric tides I + II. In: J. Geophys. Res. 87, 1980, S. 5222, 5241.

[4] R. S. Stolarski, P. B. Hays, R. G. Roble: Atmospheric Heating by Solar EUV Radiation. In: Journal of Geophysical Research. Band 80, Nr. 16, 1975, S. 2266–2276, doi:10.1029/JA080i016p02266.

[Chapman-5] S. Chapman, R.S. Lindzen: Atmospheric Tides. D. Reidel, Dordrecht 1970.

[VollandTP-6] H. Volland: Atmospheric Tidal and Planetary Waves. Kluwer Publ., Dordrecht 1988.

[7] M. S. Longuet-Higgins: The eigenfunctions of Laplace's equations over a sphere. In: Phil. Trans. Roy. Soc. London, A262, 1968, S. 511.

[8] J. R. Holton, W.M. Wehrbein: A numerical model of the zonal mean circulation of the middle atmosphere. In: Pageoph. 118, 1980, S. 284.

[9] H. Kohl, J. W. King In: J. Atm. Terr. Phys. 29, 1967, S. 1045.

[10] Manfred Siebert: Atmospheric Tides. In: Advances in Geophysics. Volume 7. Elsevier, 1961, ISSN 0065-2687, S. 105–187.

[VollandSR-11] H. Volland: Atmosphere and earth's rotation. In: Surv. Geophys. 17, 1996, S. 1001.

[Murgatroyd-12] R. J. Murgatroyd: The structure and dynamics of the stratosphäre. In: G. A. Coby (Hrsg.): The Global Circulation of the Atmosphere. In: Roy. Met. Soc. London, 1969, S. 159.

[13] H. Fortak: Meteorologie. Deutsche Buchgemeinschaft, Berlin 1971.

[14] J. R. Holton: An Introduction to Dynamic Meteorology. Academic Press, New York 1992.

[15] D. S. Robertson: Geophysical applications of Very-Long-Baseline Interferometry. In: Rev. Modern Phys. 14, 1993, S. 1.

[16] T. M. Eubanks, J.A. Steppe, J.O. Dickey, P.S. Challahan: A spectral analysis of earths angular momentum budget. In: J. Geophys. Res. 90, 1985, S. 53787.

[17] R. D. Rosen: The axial momentum balance of earth and its fluid envelop. In: Surv. Geophys. 14, 1993, S. 1.

[18] W. E. Carter, D.S. Robinson: Studying the earth by very-long-baseline interferometry. In: Sci. American. 44, 1986, S. 225.

[19] R. Hide, J. O. Dickey: Earth's variable rotation. In: Sciences. 235, 1991, S. 629.

[20] W. Köhnlein: A model of thermospheric temperature and composition. In: Planetary and Space Science. Band 28, Nr. 3, März 1980, S. 225–243, doi:10.1016/0032-0633(80)90015-X.

[21] U. von Zahn, W. Köhnlein, K. H. Fricke, U. Laux, H. Trinks, H. Volland: Esro 4 model of global thermospheric composition and temperatures during times of low solar activity. In: Geophysical Research Letters. Band 4, Nr. 1, 1977, S. 33–36, doi:10.1029/GL004i001p00033.