Stochastisches Tunneln

Stochastisches Tunneln (STUN) ist eine Methode zur globalen Optimierung, in der die zu minimierende Funktion mit der Monte-Carlo-Methode abgetastet wird.

Prinzip

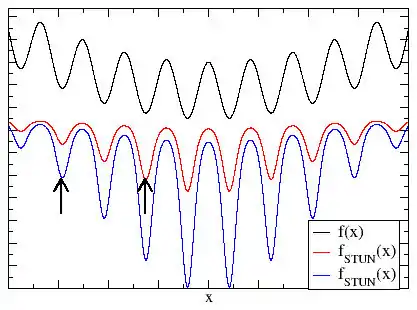
Schematische eindimensionale Testfunktion (Schwarz) und effektives STUN-Potential (Rot und Blau), wobei das mit Pfeilen markierte Minimum das beste bisher gefundene Minimum darstellt. Alle Potentialtöpfe, die über dem besten gefundenen Minimum liegen, sind unterdrückt[1]. Wenn der dynamische Prozess dem Potentialtopf um das aktuelle Minimum entkommen kann, wird er nicht von anderen, höheren lokalen Minima aufgefangen. Potentialtöpfe mit niedrigeren Minima sind verstärkt, was den dynamischen Prozess beschleunigt.

Optimierungsalgorithmen, die auf der Monte-Carlo-Methode beruhen, tasten die untersuchte Funktion ab, indem sie zufällig von der aktuellen Lösung zu einer anderen Lösung springen, wobei die Funktionswerte sich um $\Delta E$ unterscheiden. Als Wahrscheinlichkeit für solch einen Versuchssprung wird meist das als $\min \left(1;\exp \left(-\beta \cdot \Delta E\right)\right)$ definierte Metropolis-Kriterium gewählt, wobei der Parameter $\beta$ passend gewählt wird.

Das Prinzip von STUN ist, die langsame Dynamik von ungünstig geformten Energiefunktionen, die zum Beispiel in Spingläsern angetroffen werden[2], zu umgehen, indem solche Barrieren durchtunnelt werden. Dieses Ziel wird durch die Monte-Carlo-Abtastung[3] der transformierten Funktion erreicht, die dieser langsame Dynamik nicht unterliegt. Die Transformation ist in der "Standardform" definiert durch $f_{STUN}:=1-\exp \left(-\gamma \cdot \left(f(x)-f_{o}\right)\right)$ , wobei $f_{o}$ der bislang niedrigste gefundene Funktionswert ist. Diese Transformation bewahrt die geometrischen Orte der Minima. Der Effekt solch einer Transformation ist in der Abbildung dargestellt.

Eine adaptive Variante des Verfahrens gestattet es, die Parameter des Verfahrens selber "online" zu schätzen und dadurch die Effizienz des Algorithmus zu verbessern[4].

Andere Ansätze

Simulierte Abkühlung
Parallel tempering
Evolutionärer Algorithmus
Differential evolution

Einzelnachweise

K. Hamacher and W. Wenzel: The Scaling Behaviour of Stochastic Minimization Algorithms in a Perfect Funnel Landscape. Phys. Rev. E 59(1):938-941, 1999
W. Wenzel and K. Hamacher: A Stochastic tunneling approach for global minimization. Phys. Rev. Lett. 82(15):3003-3007, 1999
Metropolis, M. ; Rosenbluth, A. ; Rosenbluth, M. ; Teller, A. ; Teller, E.: Equation of state calculations by fast computing machines. J. Chem. Phys 21 (1953), S. 1087–1092
K. Hamacher: Adaptation in Stochastic Tunneling Global Optimization of Complex Potential Energy Landscapes. Europhys. Lett. 74(6):944, 2006

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] K. Hamacher and W. Wenzel: The Scaling Behaviour of Stochastic Minimization Algorithms in a Perfect Funnel Landscape. Phys. Rev. E 59(1):938-941, 1999

[2] W. Wenzel and K. Hamacher: A Stochastic tunneling approach for global minimization. Phys. Rev. Lett. 82(15):3003-3007, 1999

[3] Metropolis, M. ; Rosenbluth, A. ; Rosenbluth, M. ; Teller, A. ; Teller, E.: Equation of state calculations by fast computing machines. J. Chem. Phys 21 (1953), S. 1087–1092

[4] K. Hamacher: Adaptation in Stochastic Tunneling Global Optimization of Complex Potential Energy Landscapes. Europhys. Lett. 74(6):944, 2006