David Marr

David Marr (* 19. Januar 1945 in Essex; † 17. November 1980 in Cambridge (Massachusetts)) war ein englischer Psychologe, Informatiker und Mathematiker. Er gilt als einer der Begründer der Neuroinformatik und entwickelte ein Modell des Sehens als Informationsverarbeitung des Gehirns, die nach den Prinzipien der elektronischen Datenverarbeitung eines Computers funktioniert.

Der Marr Prize wurde nach ihm benannt und wird alle zwei Jahre auf der International Conference on Computer Vision (ICCV) vergeben.

Leben

Ausgebildet an der Rugby School studierte Marr Mathematik und Neuroinformatik an der Universität Cambridge, an der er 1971 bei Giles Brindley promoviert wurde (A general theory for cerebral cortex).[1] Später war er Professor am Massachusetts Institute of Technology. Unheilbar an Leukämie erkrankt, schrieb er unter großen Anstrengungen am Ende seines Lebens an seinem Hauptwerk Vision, das erst zwei Jahre nach seinem Tod unter Mithilfe vieler Kollegen erschien.

1979 erhielt er den IJCAI Computers and Thought Award.

Werk

Marr verknüpfte Ergebnisse der Psychologie, Künstlichen Intelligenz und Neurophysiologie zu einem neuen Modell der Funktionsweise des Sehens. Für ihn ist Sehen eine Informationsverarbeitung des Gehirns, das gar nicht mit Bildern operiert, deren Licht ja bereits auf der 2-dimensionalen Netzhaut gestoppt und von ihr in neuronale Aktivität umgewandelt wird. Diese elektrischen Aktivitätsmuster repräsentieren die Außenwelt und werden erst im Gehirn zu dem kombiniert, was wir Sehen nennen. Um diesen Prozess zu verstehen, muss man nach Marr Fragen auf drei Ebenen klären:

der Rechenebene (computational level): Welchen Zweck hat das Sehen? Was soll es leisten?
der algorithmischen Ebene (algorithmic level): Wie kann das Ziel der Rechenebene erreicht werden, d. h. wie können Eingangs- und Ausgangsdaten genau dargestellt werden, und wie lautet der Algorithmus, der die Eingangsdaten in die Ausgangsdaten transformiert?
der technischen Ebene (implementational level): Wie wird der Algorithmus physiologisch bzw. physikalisch als neuronale Aktivität realisiert?

Diese Unterscheidungen Marrs erlangten in der Folge auch Bedeutung in anderen Disziplinen, so bei Design und Analyse künstlicher neuronaler Netze.

Sehen als die Verarbeitung von zweidimensionalen Daten der Netzhaut (Retina) zu einer dreidimensionalen Beschreibung der Welt ist nach Marr ein Prozess, der in vier Stufen abläuft:

Grundlage ist das retinale Bild, eine Projektion der Außenwelt, die Helligkeits- oder Farbinformationen in Form eines Intensitätsbildes enthält;
der erste Entwurf ("sketch", Skizze), in dem durch Analyse der Helligkeitsänderungen Kanten, zusammenhängende Flächen und Oberflächentexturen nach Art einer Strichzeichnung erkannt werden;
der 2½-D-Entwurf, der durch Kombination der beiden retinalen Informationen entsteht und die räumliche Orientierung und grobe Tiefe von Oberflächen bestimmt, so dass ein erstes grobes Bild von der dreidimensionalen Welt entsteht.
das 3-D-Modell, das mit der Querdisparation der beiden retinalen Bilder eine genaue Information über die Tiefe ergibt, so dass die Wahrnehmung trotz aller Augen- und Körperbewegungen stabil bleibt.

Das Marr-Wavelet

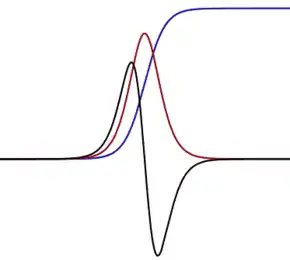
Schematische Darstellung einer Helligkeitskurve an einer Kante (blaue Kurve), ihrer ersten Ableitung (rot) und ihrer zweiten Ableitung (schwarz). Die Nullstelle der zweiten Ableitung lokalisiert nach Marr die Kante.

Obschon Marrs Modell des Sehens umstritten ist, so lieferte es als Nebenprodukt einen wichtigen Beitrag zur erst Ende der 1980er Jahre entstehenden Theorie der Wavelets. Insbesondere zur Erkennung von Kanten sind nach Marr die Nullstellen der zweiten Ableitung der Helligkeitsfunktion entscheidend, also ihre Wendepunkte, siehe nebenstehende Abbildung. Da die Retina ein zweidimensionales Bild liefert, führt dieser Ansatz mathematisch auf die zweite Ableitung der zweidimensionalen Gaußschen Normalverteilung als Filterfunktion,

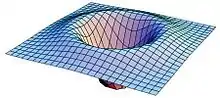
\psi (x,y)=-{\frac {1}{\pi \sigma ^{4}}}\left(1-{\frac {x^{2}+y^{2}}{2\sigma ^{2}}}\right)\mathrm {e} ^{-(x^{2}+y^{2})/2\sigma ^{2}}.

Heute nennt man diese Funktion oft Marr-Wavelet, es ist der mit (−1) multiplizierte und wegen seiner Form sogenannte Mexikanische Hut:

Das zweidimensionale Marr-Wavelet

Siehe auch

Marr-Hildreth-Operator

Literatur

Rainer Guski (1996): Wahrnehmen – ein Lehrbuch, Kohlhammer Stuttgart Berlin Köln, ISBN 3-17-011845-5, §2.8.1
Stéphane Jaffard, Yves Meyer und Robert R. Ryan (2001): Wavelets. Tools for Science and Technology, SIAM Philadelphia, ISBN 0-89871-448-6, §8
David Marr (1982): Vision. A Computational Investigation into the Human Representation and Processing of Visual Information, W. H. Freeman and Company, ISBN 0-7167-1284-9.

Weblinks

Online-Biographie (englisch)

Einzelnachweise

David Marr im Mathematics Genealogy Project (englisch)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] David Marr im Mathematics Genealogy Project (englisch)