Skalenniveau
Das Skalenniveau oder Messniveau oder die Skalendignität (selten Skalenqualität) ist in der Empirie eine wichtige Eigenschaft von Merkmalen bzw. von Variablen.
Systematik der Skalen
Je nach der Art eines Merkmals bzw. je nachdem, welche Vorschriften bei seiner Messung eingehalten werden können, lassen sich verschiedene Stufen der Skalierbarkeit unterscheiden:
| Skalenniveau | logische / mathematische Operationen | Messbare Eigenschaften | Beispiel | [zusätzliche] Lageparameter | |
|---|---|---|---|---|---|
| Nominalskala | =/≠ | Häufigkeit | Postleitzahlen[1], Geschlechter | Modus | |
| Ordinalskala | =/≠ ; </> | Häufigkeit, Rangfolge | Schulnoten („sehr gut“ bis „ungenügend“), Tabellenplatz in der Bundesliga | Median | |
| Kardinalskala | |||||
| Intervallskala | =/≠ ; </> ; +/− (Merkmal + Merkmalsdifferenz) | Häufigkeit, Rangfolge, Abstand | Zeitskala (Datum), Intelligenzquotient, Temperatur (in Grad Celsius) | Arithmetisches Mittel | |
| Verhältnisskala | =/≠ ; </> ; +/− ; ÷ (liefert einheitenlose Zahl) / x (Zahl x Merkmal) | Häufigkeit, Rangfolge, Abstand, natürlicher Nullpunkt | Alter (in Jahren), Umsatz (in Euro), Temperatur (in Kelvin) | Geometrisches Mittel | |
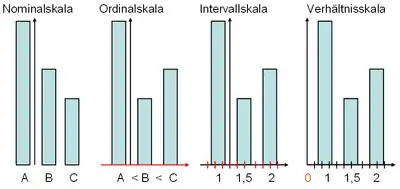
Intervall- und Verhältnisskala werden zur Kardinalskala zusammengefasst. Merkmale auf dieser Skala werden dann als metrisch bezeichnet. Nominal- oder ordinalskalierte Merkmale (s. u.) bezeichnet man auch als kategorial.
Das Skalenniveau bestimmt,
- welche (mathematischen) Operationen mit einer entsprechend skalierten Variable zulässig sind. Dabei können Operationen, die bei Variablen eines bestimmten Skalenniveaus zulässig sind, grundsätzlich auch auf Variablen aller höheren Skalenniveaus durchgeführt werden. Ein auf einem bestimmten Niveau skalierbares Merkmal kann auf allen darunter liegenden Skalenniveaus dargestellt werden, jedoch nicht umgekehrt.
- welche Transformationen mit entsprechend skalierten Variablen durchgeführt werden können, ohne Information zu verlieren bzw. zu verändern.
- welche Information das entsprechende Merkmal liefert, welche Interpretationen Ausprägungen des entsprechenden Merkmals zulassen.
Das Skalenniveau gibt keine Auskunft darüber,
- ob eine Variable diskret (kategorial) oder stetig ist[2] (siehe Hauptartikel Merkmal). Lediglich bei der Nominalskalierung ist das Merkmal grundsätzlich nicht stetig, sondern diskret.[3]
„Obwohl Skalenniveau und Anzahl der möglichen Ausprägungen unabhängige Konzeptionen darstellen, sind in der Praxis nominal- und ordinalskalierte Merkmale meist diskret und metrisch skalierte Merkmale meist stetig.“[2]
Geschichte der Einteilung
„Skalen können danach klassifiziert werden, welche Transformationen für sie zulässig sind.“[4] Diese Klassifikation von Skalen sei aber nicht unumstritten, Kritik hierzu finde man vor allem bei Prytulak (1975)[5] und Duncan[6][4] (s. a. Michell[7]). „Da es unendlich viele zulässige Transformationen einer bestimmten Skala gibt, könnten prinzipiell auch unendlich viele verschiedene Skalenniveaus unterschieden werden. Die meist verwendete Klassifikation geht auf Stevens (1946)[8] zurück. Dieser unterscheidet Nominal-, Ordinal-, Intervall- und Ratioskalen“.[4] „Eine detailliertere Klassifikation zum Beispiel von Narens und Luce (1986)[9] oder von Orth (1974)[10] enthalte meist noch eine ‚Log-Intervallskala‘ zwischen der Intervall- und der Ratioskala. Bei einer Log-Intervallskala sind noch Potenztransformationen (x'= s * xr; mit s und r größer 0) zulässig.“[4]
Marks (1974)[11] versucht die Möglichkeiten verschiedener Skalenniveaus systematisch zu erfassen. Er schlägt dazu eine allgemeine Transformationsfunktion vor, in der drei Konstanten frei gewählt werden können. Die Konstanten können jeweils entweder positiv (+) oder Null (0) sein. Null zeigt an, dass eine Skalentransformation hier zu einem Informationsverlust führen würde. Ein Pluszeichen zeigt an, dass eine solche Transformation ohne Informationsverlust möglich wäre. Die von ihm vorgeschlagene allgemeine Formel lautet:
x'=(a+1)x(b+1)+c
Beispielsweise müssten für eine Intervallskala die Konstanten a positiv, b null, c positiv sein. Damit ergibt sich für eine Intervallskala die Lineartransformation als allgemein zulässige Transformationsregel:
x'=ax+b
Dementsprechend kommt Marks auf folgende 8 Skalen, wobei zu sehen ist, dass die Aussagekraft steigt, während gegenläufig die Transformationsmöglichkeiten ohne Informationsverlust abnehmen:
| (engl.) Skalenbezeichnung | a | b | c | Anzahl zulässiger Transformationen | Aussagekraft |
|---|---|---|---|---|---|
| Ordinal | + | + | + | 3 | 0 |
| Hyperordinal | 0 | + | + | 2 | 1 |
| Interval | + | 0 | + | 2 | 1 |
| Log interval | + | + | 0 | 2 | 1 |
| Difference | 0 | 0 | + | 1 | 2 |
| Power | 0 | + | 0 | 1 | 2 |
| Ratio | + | 0 | 0 | 1 | 2 |
| Absolute | 0 | 0 | 0 | 0 | 3 |
Nominalskala
Niedrigstes Skalenniveau. Für verschiedene Objekte oder Erscheinungen wird mithilfe eines Vergleichs lediglich eine Entscheidung über Gleichheit oder Ungleichheit der Merkmalsausprägung getroffen (z. B. x ≠ y ≠ z). Es handelt sich also nur um qualitative Merkmale (z. B. Blutgruppen oder Geschlecht). Es gilt die Gleichheitsrelation, also kann man entscheiden, ob zwei Ausprägungen gleich oder ungleich sind. Die Werte können aber nicht der Größe nach sortiert werden, im Sinne von „ist größer als“ oder „besser als“.
Ordinalskala
Für ein ordinal skalierbares Merkmal bestehen Rangordnungen der Art „größer“, „kleiner“, „mehr“, „weniger“, „stärker“, „schwächer“ zwischen je zwei unterschiedlichen Merkmalswerten (z. B. x > y > z). Über die Abstände zwischen diesen benachbarten Urteilsklassen ist jedoch nichts ausgesagt. Meist handelt es sich um qualitative Merkmale, wie z. B. der in der Frage gesuchte „höchste erreichbare Bildungsabschluss“. Ein weiteres Beispiel sind die Schulnoten: Note 1 ist besser als Note 2, es ist aber ausgesprochen zweifelhaft, ob der Unterschied zwischen Note 1 und 2 gleich groß ist wie der zwischen Note 3 und Note 4.
Eine Sonderform der Ordinalskala ist die Rangskala. Hierbei kann jeder Wert nur einmal vergeben werden. Beispiele hierfür sind die Erreichung von Rängen im Sport, genauso wie bei anderen Leistungsvergleichen, oder die natürliche Ordnung, wie sie im Tierreich oft bei Lebewesen vorkommt, die in sozialen Gruppen leben wie z. B. Hühnervögel. Ihre Ordnung wird daher auch Hackordnung genannt.
Intervallskala
Die Reihenfolge der Merkmalswerte ist festgelegt, und die Größe des Abstandes zwischen zwei Werten lässt sich sachlich begründen. Als metrische Skala macht sie Aussagen über den Betrag der Unterschiede zwischen zwei Klassen. Die Ungleichheit der Merkmalswerte lässt sich durch Differenzbildung quantifizieren (z. B. beim Datum könnte das Ergebnis lauten „drei Jahre früher“). Der Nullpunkt („nach Christi Geburt“) und der Abstand der Klassen (Jahre oder Monde) sind jedoch willkürlich festgelegt. Hinweis: Bei den metrischen Skalen unterscheidet man diskrete und kontinuierliche Merkmale.
Verhältnisskala (auch Ratioskala)
Die Verhältnisskala besitzt das höchste Skalenniveau. Bei ihr handelt es sich ebenfalls um eine metrische Skala, im Unterschied zur Intervallskala existiert jedoch ein absoluter Nullpunkt (z. B. Blutdruck, absolute Temperatur, Lebensalter, Längenmaße). Einzig bei diesem Skalenniveau sind Multiplikation und Division sinnvoll und erlaubt. Verhältnisse von Merkmalswerten dürfen also gebildet werden (z. B. x = y · z).
Grauzonen zwischen den Skalenniveaus
Es existieren Merkmale, die sich nicht genau einem Skalenniveau zuordnen lassen. So könnte sich z. B. bei einem Merkmal nicht sicher belegen lassen, dass es intervallskaliert ist, man ist sich aber sicher, dass es mehr als ordinalskaliert ist. In einem solchen Fall könnte man eine Interpretation auf einer Intervallskala versuchen, diese Annahme aber bei der Interpretation berücksichtigen und dort entsprechend vorsichtig vorgehen. Ein Beispiel dafür ist die Bildung von Durchschnitten bei Schulnoten als Ziffern kodiert, die eigentlich ein ordinalskaliertes Merkmal darstellen, weil sie in festen Begriffen definiert sind, etwa von sehr gut bis ungenügend.
Andere Beispiele sind Uhrzeiten ohne Angabe des Datums (zirkadiane Daten) oder Himmelsrichtungen. Hier lassen sich innerhalb von Teilbereichen Werte ordnen und Abstände messen, und mit einer entsprechenden Beschränkung für die Größe von Abständen lassen sich sogar beliebig viele Abstände sinnvoll (genauer: ‘eindeutig’) addieren. Ohne eine Beschränkung gilt das nicht mehr („Liegt 2:00 Uhr vor oder nach 22:00 Uhr?“ – „Sowohl als auch“).
Probleme bei der Skalierung
Im Einzelfall können natürliche Ordnungen auftreten, die sich zwar prinzipiell mit einer bestimmten Skala beschreiben lassen, aber mitunter einzelne Abweichungen enthalten. Ein Beispiel sind Platzierungen bei Sportereignissen (rangskaliert), wo eigentlich jeder Sportler nur einen Platz einnimmt (erster, zweiter, dritter usw.), aber sich seinen Platz mit einem anderen Sportler teilen muss, wenn dieser exakt denselben Messwert erreicht hat. Je nach Reglement kann dann ein höherer oder niedriger gelegener Rang nicht vergeben werden, so dass die Skala eine Leerstelle aufweist, die es sonst nicht gibt (nicht vergebene Silbermedaille bei zwei ersten Plätzen). Hier liegt streng genommen eine auf Rangskalierung gemaßregelte Ordinalskala vor.
Im Tierreich sind Rangskalierungen manchmal nicht stringent, so dass es innerhalb einer aufsteigenden Hackordnung besonders im unteren Skalenbereich zwischengeschaltete Tripletts oder Multiplets gibt, die sich gegenseitig nach dem Schema A>B>C>A „hacken“. Man spricht dabei von Intransitivität. Ein solches Phänomen kann auch nicht durch Überführung in Ordinalskalenniveau erschöpfend beschrieben werden und erfordert eine vollständige Darstellung in einer Matrix oder die Zuhilfenahme eines weiteren Merkmals, z. B. Erfolg bei Futterstreit in gefressenem Futtergewicht, sofern ranghöhere Tiere stets mehr fressen als rangniedere, was jedoch oft nicht so ist. Die Matrizendarstellung wird deshalb in solchen Fällen der Skalierung vorgezogen, obgleich sie visuell schwerer erfassbar und statistisch aufwändiger zu verwenden ist.
Einzelnachweise
- Herbert Büning, Götz Trenkler: Nichtparametrische statistische Methoden. Walter de Gruyter, 1994, ISBN 978-3-11-016351-3, S. 8 (eingeschränkte Vorschau in der Google-Buchsuche).
- Gerhard Tutz: Die Analyse kategorialer Daten: anwendungsorientierte Einführung in Logit-Modellierung und kategoriale Regression. Oldenbourg Wissenschaftsverlag, München 2000, ISBN 3-486-25405-7, S. 3 (eingeschränkte Vorschau in der Google-Buchsuche).
- Wolfgang Brachinger: Multivariate statistische Verfahren. Walter de Gruyter, Berlin 1996, ISBN 3-11-013806-9, S. 11 (eingeschränkte Vorschau in der Google-Buchsuche).
- Rainer Schnell, Paul Hill, Elke Esser: Methoden der empirischen Sozialforschung. 2. Auflage. R. Oldenbourg, München/ Wien 1989, ISBN 3-486-21463-2, S. 137 (8. Auflage online)
- L. S. Prytulak: Critique of S. S. Stevens´Theory of Measurement Scales classification. In: Perceptual and Motor Skills. 1975 (41, 3, 28).
- vermutlich O. D. Duncan: Notes on Social Measurement. Historical and Critical. Russell Sage Foundation, New York 1984, ISBN 0-87154-219-6, S. 119–156
- J. Michell: Measurement scales and statistics: a clash of paradigms. In: Psychological Bulletin. 100, Nr. 3, 1986, S. 398–407. doi:10.1037/0033-2909.100.3.398.
- S. S. Stevens: On the Theory of Scales of Measurement. In: Science. 1946, 103, S. 677–680. (online)
- L. Narens, R. D. Luce,: Measurement: The Theory of Numerical Assignments. In: Psychological Bulletin. 1986, 99, 2, S. 166–180. (online) (PDF; 1,5 MB)
- B. Orth: Einführung in die Theorie des Messens. Kohlhammer, Stuttgart/ Berlin/ Köln/ Mainz 1974, ISBN 3-17-002055-2.
- Lawrence E. Marks: Sensory Processes: The New Psychophysics. Academic Press, New York 1974, ISBN 0-12-472950-9, S. 247–249.
Literatur
- L. Fahrmeir, A. Hamerle, G. Tutz (Hrsg.): Multivariate statistische Verfahren. 2., überarbeitete Auflage. Walter de Gruyter, Berlin/ New York 1996, ISBN 3-11-013806-9.
- L. Fahrmeir, R. Künstler, I. Pigeot, G. Tutz: Statistik. Der Weg zur Datenanalyse. Springer, Berlin/ Heidelberg/ New York 1999, ISBN 3-540-67826-3.
- S. H. Kan: Metrics and Models in Software Quality Engineering. 2. Auflage. Pearson Education, Boston 2003, ISBN 0-201-63339-6.
- K. Backhaus, B. Erichson, W. Plinke, R. Weiber: Multivariate Analysemethoden. Eine anwendungsorientierte Einführung. 11. Auflage. Springer-Verlag, Berlin u. a. 2005, ISBN 3-540-27870-2, S. 4–6.
- Jürgen Bortz: Statistik für Human- und Sozialwissenschaftler. 6. Auflage. Springer, 2005, ISBN 3-540-21271-X, S. 15–27.