Lewis Fry Richardson
Lewis Fry Richardson (* 11. Oktober 1881 in Newcastle upon Tyne; † 30. September 1953 in Kilmun, Argyll) war ein britischer Meteorologe und Friedensforscher. Er berechnete die erste Wettervorhersage.[1] Auch wenn sein Ergebnis weit vom tatsächlichen Wettergeschehen abwich, begründete er damit die Methode der numerischen Wettervorhersage. Einige seiner Erkenntnisse nahmen Ergebnisse der Chaostheorie voraus.
Als überzeugter Quäker und Pazifist wechselte er in den 1920er Jahren in die Friedensforschung, in die er quantitative Methoden einführte.
Leben
Jugend und Ausbildung
Lewis war das jüngste von sieben Kindern des Gerberei-Unternehmers David Richardson und seiner Frau Catherine, geborene Fry; die Familie gehörte seit dem 17. Jahrhundert zu den Quäkern. Nach dem Besuch der Grundschule in Newcastle ging er ab 1894 auf die Bootham Schule in York, die 1823 für Söhne wohlhabender Quäker gegründet worden war. Ab 1898 besuchte er zwei Jahre lang das Durham College of Science in Newcastle, wo er Mathematik, Physik, Chemie, Botanik und Geologie belegte. Er schloss es mit dem Associate of Science – vergleichbar den heutigen A-levels – ab. Danach nahm er ein Studium am King’s College, Cambridge auf, ohne sich auf eine bestimmte Naturwissenschaft zu spezialisieren. 1903 legte er Teil I des Tripos in Naturwissenschaften ab.
Lehr- und Wanderjahre
Seine erste Anstellung fand Richardson 1903 als Assistent in der Physikalischen Abteilung des National Physical Laboratory (in Deutschland vergleichbar der Physikalisch-Technischen Bundesanstalt), wo er Stahllegierungen auf ihre Zugfestigkeit prüfte. Nach nur einem Jahr wechselte er als Physikdozent an das University College in Aberystwyth, wo er ebenfalls nicht lange blieb. 1906 ging er als Chemiker in die Industrie zu einer kleinen Torffirma, die National Peat Industries Ltd. in Newcastle upon Tyne. Richardson und sein Vater beteiligten sich mit beträchtlichen Summen an dieser Firma. Hier bearbeitete er ein mathematisches Problem, das für seine spätere Karriere wichtig wurde: Er entwickelte ein grafisches Verfahren zur näherungsweisen Lösung von Differentialgleichungen, um zu berechnen, wie am besten die Gräben zur Entwässerung von Torfmooren gezogen werden sollten. Dies führte 1910 zu seiner ersten wissenschaftlichen Publikation in den Philosophical Transactions of the Royal Society, wobei er hier die Methode auf Spannungen in Staumauern anwendete. Es ist nicht ganz klar, wann Richardson seinen Arbeitsplatz in der Torfindustrie verließ, aber 1907 war er für kurze Zeit Assistent bei dem Biometriker Karl Pearson, dessen eugenische Ideale er teilte. Dann kehrte er an das National Physical Laboratory, diesmal in die Metrologie-Abteilung, zurück, wo er zwei Jahre lang blieb.
1908 lernte er seine künftige Frau Dorothy, geborene Garnett, kennen. Die beiden heirateten Anfang 1909. Obwohl Dorothy nicht aus einer Quäkerfamilie kam, engagierte sie sich später stark in dieser Glaubensgemeinschaft. Wegen einer Rhesus-Inkompatibilität erlitt sie zahlreiche Fehlgeburten, sodass die Ehe kinderlos blieb. Das Ehepaar adoptierte schließlich drei fremde Kinder. Auch in Jahren, in denen Richardson gut verdiente, führten sie immer einen bescheidenen Haushalt, weil nach Überzeugung der Quäker kein Geld auf Kleidung oder Essen verschwendet werden soll.
1909 wurde Richardson Leiter des Chemischen und Physikalischen Labors der Sunbeam Lamp Company in Gateshead. Wieder beteiligten er und sein Vater sich am Aktienkapital. Der Untergang der Titanic am 15. April 1912 beschäftigte Richardson – wie auch eine Reihe anderer Erfinder – so sehr, dass er eine Art von Sonar-Technik über Wasser entwickelte (Britisches Patent Nr. 9423 von 1912). Im Dezember meldete er ein weiteres Patent (Nr. 11125) an, in dem er dieselbe Technik unter Wasser beschrieb, also ein vollgültiges Sonar. Für beide Ideen fand er jedoch keine Geldgeber, die es ermöglicht hätten, die Patente auszuwerten.
Nach drei Jahren in Gateshead wechselte Richardson als Dozent an die Municipal School of Technology in Manchester, eine kommunale Einrichtung, die meist von Abendschülern besucht wurde. Aus seinen Tagebüchern geht hervor, dass er hier große Probleme hatte, Disziplin unter seinen Schülern zu schaffen. Nach einigen Monaten bewarb er sich 1913 erfolgreich als Leiter des Observatoriums Eskdalemuir des britischen Wetterdiensts. Weil hier vor allem geomagnetische Beobachtungen durchgeführt werden sollten, war das Observatorium in einer entlegenen Gegend Schottlands errichtet worden, was Richardsons Bedürfnis nach Einsamkeit entgegenkam. Mit der Stelle war ausdrücklich die Möglichkeit zur Grundlagenforschung verbunden. Bis dahin hatte Richardson sich nicht mit Meteorologie beschäftigt; 1915 entwickelte er hier die ersten Ideen für eine numerische Wettervorhersage (siehe unten).
Als Pazifist im Ersten Weltkrieg
Als Quäker war Richardson ein überzeugter Pazifist. Zum ersten Mal geriet er damit in Schwierigkeiten, als er aufgefordert wurde, in Eskdalemuir eine Methode zur Lokalisierung von Artilleriegeschützen zu entwickeln. 1916 löste er weitere absehbare Konflikte, indem er kündigte und für eine Krankenwagen-Einheit der Quäker (Friends Ambulance Unit) einen Krankenwagen an der Westfront fuhr. Hier liegen die Wurzeln seiner lebenslangen Beschäftigung mit Krieg und Frieden.
Nach dem Ersten Weltkrieg bewarb sich Richardson wieder beim britischen Wetterdienst, diesmal um die Stelle in Benson. Dies war eines der wenigen Observatorien, von denen aus die höheren Luftschichten untersucht wurden. Richardson begann hier mit seiner Arbeit im März 1919 und arbeitete vor allem an der Verbesserung von Wetterballons. Schon im folgenden Jahr geriet er jedoch in einen Gewissenskonflikt, als der britische Wetterdienst dem Luftfahrtministerium, das für die Luftwaffe zuständig war, untergeordnet wurde. Im Sommer 1920 kündigte Richardson aus diesem Grund seine Stelle. Sir Nelson Johnson, ein späterer Direktor des britischen Wetterdiensts, hat diese Entscheidung als „eine der Tragödien in der Geschichte der Meteorologie“[2] bezeichnet.
Nach Angaben seiner Frau hat Richardson später einen Teil seiner unveröffentlichten Arbeiten vernichtet, als ihm klar wurde, dass sie Militärforschern in Porton Down zur Beurteilung des Verhaltens von Giftgaswolken nützlich gewesen wären.
Ein Fellow der Royal Society arbeitet an kleinen Colleges
Richardson wurde Dozent für Physik und Mathematik am Westminster Training College. In dieser Zeit begann er ein zweites Studium der Psychologie und Mathematik (B.Sc. in Psychologie und Mathematik 1925). Er übersprang den M.Sc., weil dieser akademische Grad im Ruch stand, käuflich zu sein, und promovierte 1926 gleich zum D.Sc. Im selben Jahr wurde er zum Fellow der Royal Society (F.R.S.) berufen – die höchste wissenschaftliche Ehre, die in Großbritannien vergeben wird. In diesem Jahr entschied sich Richardson jedoch auch, endgültig die physikalisch-meteorologische Forschung zu verlassen und sich der Psychologie widmen. Hier arbeitete er in seiner knappen Freizeit vor allem über Fragen der Psychophysik.
1929 wurde er Direktor des Technical College im schottischen Paisley. Der Verwaltungsrat konnte sein Glück kaum fassen, dass sich ein F.R.S. überhaupt für so eine Stelle, die mit einer immensen Unterrichtsverpflichtung verbunden war, interessierte. Nach der „Machtergreifung“ der Nationalsozialisten in Deutschland halfen die Richardsons einer Reihe von deutschen Emigranten, in Großbritannien Fuß zu fassen. Durch die politische Lage beunruhigt, verlagerte Lewis Richardson seine Aktivitäten zunehmend in die Friedensforschung. Im August 1939, wenige Wochen vor Beginn des Zweiten Weltkriegs, besuchte er Danzig, um sich selbst einen Eindruck von der Lage zu machen, und reiste über Berlin zurück.
Im Februar 1940 kündigte Richardson seine Stelle am Technical College, um sich vollständig der Friedensforschung zu widmen. Der Verwaltungsrat erlaubte der Familie, weiterhin im Direktorenhaus wohnen zu bleiben; weil Richardson nunmehr von seinen Ersparnissen lebte, musste sich die Familie trotzdem sehr einschränken.
Werk
Die erste numerische Wettervorhersage
Richardson hatte sich erstmals 1915 in Eskdalemuir mit der Idee einer numerischen Wettervorhersage beschäftigt. 1916 hatte er den ersten Entwurf seines Buchs Weather Prediction by Arithmetical Finite Differences vollendet, wollte es jedoch noch um ein praktisches Beispiel ergänzen. Die Gelegenheit ergab sich während seines Diensts als Krankenwagenfahrer an der Westfront. Er benötigte sechs Wochen, um die Veränderung des Wetters an zwei Orten innerhalb der nächsten sechs Stunden zu berechnen. Der Fehler war so groß, dass das Ergebnis praktisch nicht verwendbar war, doch handelt es sich um den ersten Versuch einer numerischen Wettervorhersage. Das Buch erschien schließlich 1922 unter dem Titel Weather Prediction by Numerical Process und gilt heute als Klassiker.
Zur Zeit von Richardson war schon lange bekannt, dass Wetter den Gesetzen der Physik unterliegt. Die Meteorologen erstellten ihre Wettervorhersagen jedoch aufgrund ihrer Erfahrung mit ähnlichen Wetterlagen, und physikalische Argumente spielten dabei kaum jemals eine Rolle. Bereits 1904 hatte Vilhelm Bjerknes eine numerische Wettervorhersage gefordert, ohne einen praktikablen Weg zeigen zu können. Das erste Problem war, dass kaum Messwerte aus den höheren Luftschichten gewonnen wurden. Zweitens lagen die Gleichungen, die das physikalische Geschehen in der Atmosphäre beschrieben, nicht in einer für Routine-Vorhersagen brauchbaren Form vor. Drittens hätten die Rechnungen eine Zeit benötigt, in der die Vorhersage schon längst von der Realität überholt worden wäre. Lewis Richardson schöpfte jedoch Mut aus der Präzision der Nautischen Jahrbücher, in denen die Position der Gestirne exakt vorhergesagt wurde, ebenfalls ohne dass sich ihre Konstellationen jemals wiederholten.
Die International Meteorological Organization – der Vorgänger der World Meteorological Organization – hatte für die meteorologische Forschung Tage bestimmt, an denen an möglichst vielen Orten der Welt Wetterballons aufsteigen sollten, um wenigstens für diese Tage Daten aus den oberen Luftschichten zu erheben. Richardson griff für seine Vorhersage auf die Unterlagen zum 20. Mai 1910, 7 Uhr Greenwich Mean Time zurück. Für seine numerische Wettervorhersage überzog er die Wetterkarte von Europa mit einem Schachbrettmuster, wobei die Felder eine Seitenlänge von etwa 200 Kilometer hatten. Die Atmosphäre oberhalb jedes dieser Felder unterteilte er weiter in Schichten mit Grenzen in 2,0, 4,2, 7,2 und 11,8 Kilometern Höhe. Beinahe die Hälfte seines Buches Weather Prediction by Numerical Process besteht dann aus einer Diskussion der notwendigen physikalischen Gleichungen, um möglichst alle physikalischen Vorgänge, die sich zwischen diesen Zellen abspielen, zu berücksichtigen. Ausgiebig beschäftigte sich Richardson außerdem mit dem Problem der Turbulenz. Mit diesem Handwerkszeug versuchte er für zwei Felder in der Mitte des Schachbrettmusters die Änderungen von Luftdruck, Wind und Temperatur in den folgenden sechs Stunden zu berechnen. Das Ergebnis war grotesk falsch: So änderte sich in einem Feld der Luftdruck um 145 Millibar – der Unterschied zwischen dem höchsten und dem niedrigsten Luftdruck, der je auf den Britischen Inseln gemessen worden war, betrug jedoch nur 130 Millibar. Trotzdem hat Richardson in seinem Buch zum ersten Mal gezeigt, wie eine numerische Wettervorhersage im Prinzip ablaufen könnte.
Am Schluss präsentierte er eine Vision, wie es mit Hilfe einer Organisation von 64.000 „Computern“ – damals waren mit diesem Begriff noch Menschen gemeint – möglich sein müsste, das weltweite Wetter so schnell zu berechnen, dass tatsächlich eine Wettervorhersage möglich würde. Das Buch wurde bei seiner Veröffentlichung mit viel Lob aufgenommen, aber fast alle Rezensenten betonten auch, dass die vorgestellte Methode unpraktikabel sei. Aus diesem Grund wurde es kaum in den Lehrbüchern der Meteorologie berücksichtigt und geriet schnell in Vergessenheit. Erst die Erfindung des Computers im Sinne einer Maschine hat Richardsons Vision praktikabel gemacht. Heute beruhen alle Wettervorhersagen auf der numerischen Methode. In der numerischen Mathematik ist die von ihm entwickelte Richardson-Extrapolation nach ihm benannt.
Quantitative Friedensforschung
Richardsons Beitrag zur Friedensforschung besteht darin, dass er sich fragte „kann mathematische Sprache […] das Verhalten von Menschen […] im Krieg ausdrücken?“.[3] Mathematik war zwar in einigen Zweigen der Sozialwissenschaften wie den Wirtschaftswissenschaften bereits im Gebrauch, bis dahin aber nicht in der Friedensforschung. Zum ersten Mal entwickelte Richardson seine Ideen in dem Artikel The Mathematical Psychology of War von 1919. Da es damals keine Institutionen gab, die sich mit Friedensforschung beschäftigten, schickte er das Manuskript an Bertrand Russell, der enthusiastisch reagierte, aber auch keinen Verleger finden konnte. Richardson ließ es schließlich auf eigene Kosten drucken.
Eine Theorie des Rüstungswettlaufs
1935 kam Richardson durch die Ereignisse in Deutschland wieder auf die Friedensforschung zurück. In einigen Briefen an die Zeitschrift Nature skizzierte er, wie ein Rüstungswettlauf in eine mathematische Form gefasst werden könnte. Ähnlich wird heute in der Spieltheorie argumentiert. Richardson war überzeugt, dass man durch Mathematisierung präzisere Fragen stellen konnte. Sein Buch Generalized Foreign Politics – von dem er später meinte, er hätte es besser „Theorie des Rüstungswettlaufs“ nennen sollen – erschien im Juni 1939. Für die Zeit vor dem Ersten Weltkrieg konnte er hier zeigen, welcher mathematischen Funktion die Rüstungsausgaben der späteren Kriegsgegner gefolgt war. In der Physik wurde die Explosion von entzündlichen Gasen durch eine ähnliche Funktion beschrieben. In dieser Sicht erhielt Krieg eine naturgesetzhaft ablaufende Unvermeidlichkeit. Richardson wies aber auch darauf hin, dass man durch einen simplen Vorzeichenwechsel seine Theorie auch als eine Theorie der Kooperation verwenden konnte.
Statistische Analyse kriegerischer Konflikte
Bisher hatte Richardson eher deduktiv gearbeitet, nun versuchte er sich dem Phänomen des Kriegs statistisch zu nähern. Er suchte sich zu allen kriegerischen Konflikten die statistischen Daten heraus, derer er habhaft werden konnte, wie Zahl der Opfer, Kriegsparteien, ihre Sprachen und Religionen. 1941 hatte er genügend Daten gesammelt, um erste Schlussfolgerungen zu ziehen. Die Größe eines Konflikts – gemessen an der Zahl der Opfer – folgte demnach einem Potenzgesetz, wie er für die Zeit zwischen 1820 und 1929 belegen konnte (später dehnte er seine Analyse bis 1945 aus). Obwohl er sich sehr bemühte, fand er jedoch nie eine befriedigende Erklärung für diese Tatsache. Ihm fiel jedoch bei der Gelegenheit auf, dass die Größe menschlicher Besiedlungen ebenfalls einem Potenzgesetz folgte, was er in einer Mitteilung an Nature im Dezember 1941 publizierte. Als Nächstes zählte er aus, wie viele Kriege in einem Jahr begannen, und fand eine Poisson-Verteilung, was dafür spricht, dass die Wahrscheinlichkeit, dass an einem beliebigen Tag irgendwo auf der Welt ein Krieg ausbricht, immer gleich groß ist. Diese Entdeckung rechtfertigte die Arbeitshypothese, dass sich die Gesetze der Stochastik auf historische Ereignisse wie Kriege anwenden lassen[4].
Bei der Auswertung nach Staaten stellte sich heraus, dass Großbritannien am häufigsten an Kriegen beteiligt gewesen war, dicht gefolgt von Frankreich und Russland. Schließt man Staaten unter einer Million Einwohner von der Analyse aus, so waren nur Persien, Schweden und die Schweiz in diesem Zeitraum nie in einen Krieg verwickelt (definiert als Konflikt mit mehr als 3000 Todesopfern). Richardson vermutete, dass sich diese Ergebnisse durch die Zahl der Grenzen erklären ließ, die ein Staat mit anderen Staaten teilte, wobei das Britische Empire naturgemäß die meisten Grenzen hatte. Sprachunterschiede schienen beim Ausbruch kriegerischer Konflikte keine Rolle zu spielen. Allerdings schienen Länder, deren Bewohner auf beiden Seiten chinesische Schriftzeichen verwenden, seltener in Kriege verwickelt zu sein, Länder mit spanischsprachigen Bewohnern dagegen häufiger, als zu erwarten gewesen wäre. Anhänger östlicher Religionen waren seltener, Anhänger von Christentum und Islam häufiger in Kriege verwickelt, als zu erwarten gewesen wäre. Christen kämpften häufiger untereinander, während der Islam hier eher einen dämpfenden Einfluss zu haben schien, jedoch war diese Aussage nur schlecht statistisch abgesichert. Wenn Nationen Handel miteinander trieben, gerieten sie nicht so leicht in Konflikt, allerdings war dieser Effekt schwächer, als Richardson erwartet hatte.
Praktische Ratschläge
Gefragt, was man denn nun praktisch für den Frieden tun könne, gab Richardson trotz vieler Bedenken folgende Ratschläge:
- „Wenn Sie die Güte und den Mut haben, der Heilige und Helden ausmacht, versuchen Sie Gandhis Methode.
- Wenn Sie es unmöglich finden, Ihre Feinde zu lieben, versuchen Sie wenigstens, sie zu verstehen. Ein guter Weg der Einfühlung ist, die Romane und Theaterstücke zu lesen, die sie erfreuen.
- Erheben Sie keine Einwände, wenn ihre Verwandten Ausländer heiraten wollen. Solche Bindungen können helfen, die Welt zusammenzuhalten.
- Boykottieren Sie nicht Waren, nur weil sie ausländisch sind. Handel ist ein gewisser Friedensstifter.
- Entwickeln Sie eine Loyalität gegenüber einer Weltregierung.
- Denken Sie immer daran, dass einige Ihrer Vorbereitungen zur ‚Verteidigung‘, die Ihre Nation als reine Verteidigungsmaßnahmen ansieht, mit Sicherheit auf andere Nationen wie eine gefährliche Drohung wirken, gegen die sie Gegenmaßnahmen ergreifen muss. Trotzdem gibt es einige Vorbereitungen, die tatsächlich ausschließlich der Verteidigung dienen, zum Beispiel alarmieren Luftschutz-Maßnahmen unaggressive Ausländer nicht.
- Da inzwischen zur Wissenschaft der Friedensstiftung geforscht wird, halten Sie Ausschau nach neuen und besseren Techniken.“[5]
Richardson fand für seine beiden Hauptwerke Arms and Insecurity und Statistics of Deadly Quarrels keinen Verlag. Als Problem stellte sich in diesem Zusammenhang heraus, dass die Friedensforschung noch nicht institutionell verankert war und deswegen Fachzeitschriften und Buchreihen fehlten. Da Richardson seinerseits die Mittel fehlten, seine Schriften drucken zu lassen, wählte er den kostengünstigen, aber kaum gelesenen Mikrofilm. Erst Jahre nach seinem Tod erkannten Friedensforscher, welch bedeutender Vordenker Richardson auf ihrem Gebiet gewesen war und sorgten für die Veröffentlichung seiner Schriften in Buchform.
Chaostheorie
Für seine meteorologische Forschung beschäftigte sich Richardson viel mit dem Phänomen der Turbulenz. Seine Arbeit The supply of energy from and to atmospheric eddies, die er dazu 1920 in den Proceedings of the Royal Society veröffentlichte, wird noch heute zitiert. Hier legte er die Grundlage für die weitere Turbulenzforschung, indem er die heutige Vorstellung dieses Phänomens begründete. Nach seiner wegweisenden Interpretation wird bei einer turbulenten Strömung die Energie auf großer Skala zugeführt, durch den Zerfall von Wirbeln durch alle Skalen hindurch transportiert und bei kleinsten Skalen in Form von Wärme dissipiert (Energiekaskade). Die dimensionslose Kennzahl, die das Verhältnis von potentieller und kinetischer Energie angibt, wurde zu seinen Ehren Richardson-Zahl benannt.
Im Rahmen seiner Friedensforschung entdeckte Richardson das so genannte Küstenlinienparadoxon. Er hatte untersuchen wollen, wie die Länge der Grenze zweier Staaten mit der Wahrscheinlichkeit, dass diese Staaten miteinander Krieg führen, in Zusammenhang steht. Dabei fiel ihm auf, dass die Angaben zur Grenzlänge in verschiedenen Quellen erheblich voneinander abwichen. Die Ergebnisse erschienen erst posthum 1961 in der Arbeit The problem of contiguity. Der Mathematiker Benoît Mandelbrot entdeckte zufällig diesen Aufsatz, als ihn ein Bibliothekar bat, alte Bücher durchzusehen, die weggeworfen werden sollten. Nach eigener Aussage ist Mandelbrot von Richardson bei seinen Arbeiten zur fraktalen Geometrie stark beeinflusst worden. Tatsächlich besitzen natürliche Küsten keine angebbare Länge, sondern ihre Form muss als Fraktal angegeben werden.
- Zunehmend feinere Messungen der Küstenlänge Großbritanniens mit immer kürzeren, geraden Messabschnitten ergeben eine ständig wachsende Küstenlänge, die nicht gegen einen Wert konvergiert
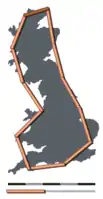Gerade Messabschnitte von 200 km Länge
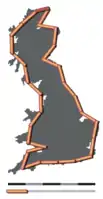Gerade Messabschnitte von 100 km Länge
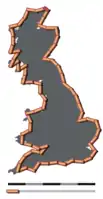Gerade Messabschnitte von 50 km Länge
Damit verwandt ist die Frage, die Richardson 1926 in seiner Arbeit Atmospheric diffusion shown on a distance-neighbour graph stellte: „Besitzt der Wind eine Geschwindigkeit?“ Er konnte zeigen, dass die Funktion, die die Position eines Moleküls im Wind beschreibt, keine Ableitung besitzt. Es ist also sinnvoll, von einer Durchschnittsgeschwindigkeit zu reden, nicht aber von einer momentanen Geschwindigkeit des Winds.
Veröffentlichungen
(Auswahl)
- The supply of energy from and to atmospheric eddies. In: Proceedings of the Royal Society A. Bd. 97, 1920, S. 354–373.
- Weather Prediction by Numerical Process. Cambridge University Press, London 1922.
- Atmospheric diffusion shown on a distance-neighbour graph. In: Proceedings of the Royal Society A. Bd. 110, 1926, S. 709–737.
- Generalized Foreign Politics. In: British Journal of Psychology Monograph Supplements. Nr. 23, 1939.
- N. Rashevsky und E. Trucco (Hrsg.): Arms and Insecurity: a mathematical study of the causes of war. Boxwood, Pittsburgh und Quadrangle, Chicago 1960 (zuvor bereits als Mikrofilm veröffentlicht).
- Quincy Wright und C. C. Lienau (Hrsg.): Statistics of Deadly Quarrels. Boxwood, Pittsburgh und Quadrangle, Chicago 1960 (zuvor bereits als Mikrofilm veröffentlicht).
- The problem of contiguity: an appendix of statistics of deadly quarrels. In: General Systems Yearbook. Bd. 6, 1961, S. 139–187.
- Oliver Ashford, Charnock, Drazin, Hunt, Smoker, Ian Sutherland (Hrsg.): Collected Papers. 2 Bände, Cambridge University Press 1993. Bd. 1: Meteorology and numerical analysis, Bd. 2: Quantitative psychology and studies of conflict.
Verschiedenes
Seit 1977 verleiht die European Geophysical Society die Lewis-Fry-Richardson-Medaille für „herausragende, allgemeine Beiträge zur nicht-linearen Geophysik“.
Literatur
- Oliver Ashford: Prophet or Professor?: Life and Work of Lewis Fry Richardson. Adam Hilger, Bristol 1985, ISBN 0-85274-774-8.
- Nils Petter Gleditsch: Lewis Fry Richardson: His Intellectual Legacy and Influence in the Social Sciences, Springer 2020, Online
- Peter Lynch: The Emergence of Numerical Weather Prediction: Richardson's Dream. Cambridge University Press 2006, ISBN 978-0-521-85729-1.
- Thomas William Körner: The Pleasures of Counting. Cambridge University Press 1996, ISBN 0-521-56823-4.
Einzelnachweise
- Christian Endt: Heiter bis tödlich. Der Brite Lewis Fry Richardson berechnete zuerst das Wetter, später packte er Kriege in Formeln. In: Süddeutsche Zeitung, 1. Oktober 2016, S. 38–39.
- zitiert nach Ashford: Prophet – or Professor? …, S. 106
- zitiert nach Ashford: Prophet – or Professor? …, S. 60
- Conflict Management and Peace Science, September 1, 2004 21: 287-296
- zitiert nach Ashford: Prophet – or Professor? …, S. 230