Kristallfeld- und Ligandenfeldtheorie

Die Kristall- und Ligandenfeldtheorie sind zwei unterschiedliche, aber sich gegenseitig ergänzende Theorien der Komplexverbindungen. Die Kristallfeldtheorie, häufig mit KFT abgekürzt, liefert ein qualitatives Verständnis und die Ligandenfeldtheorie erlaubt quantitative Voraussagen der Eigenschaften von Übergangsmetall salzen oder -komplexen. Beide Theorien erklären Struktur, Farbe und Magnetismus dieser Substanzen.

Die Kristallfeld- und die Ligandenfeldtheorie haben die quantenmechanische Behandlung des Komplexzentrums und die elektrostatische Beschreibung der Liganden gemeinsam.

Unterschiedlich ist die Vorgehensweise beider Theorien. Die Kristallfeldtheorie führt hin zur quantenmechanischen Realität der Komplexe, die Ligandenfeldtheorie geht von der quantenmechanischen Realität aus.

Zum vollständigen Verständnis der Komplexverbindungen sind weitere Theorien erforderlich. Die wichtigsten sind die Valenzbindungstheorie (VB-Theorie) und Molekülorbitaltheorie (MO-Theorie). Die VB-Theorie liefert eine Erklärung für die Komplexgeometrie, die von der Kristallfeld- und der Ligandenfeldtheorie vorausgesetzt wird. Die MO-Theorie ermöglicht ein vollständiges Verständnis des kovalenten Bindungsanteils bei Komplexen.

Struktur der Komplexverbindungen

Im Unterschied zur rein elektrostatischen Ionenbindung, z. B. bei der Salzbildung, wo sich Kationen und Anionen als Punktladungen elektrostatisch anziehen, gehen Kristallfeld- und Ligandenfeldtheorie von einer teilweise quantenmechanischen Beschreibung aus, was für die meisten Komplexverbindungen angemessener ist. In der Beschreibungsweise der Kristallfeld- und Ligandenfeldtheorie wird das Komplexzentrum quantenmechanisch behandelt, analog zur quantenmechanischen Beschreibung eines Atoms, während die Liganden, die das Komplexzentrum umgeben, rein elektrostatisch beschrieben werden. Das hat vereinfacht ausgedrückt folgende Konsequenzen:

zwischen Zentralatom und Liganden besteht eine elektrostatische Anziehung.
zwischen Zentralatom und Liganden besteht aber auch eine elektrostatische Abstoßung, weil das Komplexzentrum ein Elektronensystem mit einer quantenmechanisch bestimmten energetischen Schalenstruktur besitzt. Die Elektronen in den äußeren d-Orbitalen üben wegen ihrer negativen Ladung einen Abstoßungseffekt auf das negative geladene Ligandensystem aus.

Das Zusammenwirken von elektrostatischem Ligandenpotential und quantenmechanischer Struktur der Valenzelektronen des Zentralatoms ist sowohl für die Kristallfeld- als auch für die Ligandenfeldtheorie grundlegend.

Unterschiedlich ist die Vorgehensweise beider Theorien:

Die Kristallfeldtheorie geht von der Beschreibung der Liganden als punktförmige Ladungen aus und untersucht den Effekt des so klassisch exakt definierten Kristallfeldes auf das quantenmechanisch bestimmte Elektronensystem des Komplexzentrums (mit dem Grundzustand als reinstem Repräsentanten).
Die Ligandenfeldtheorie geht von der detaillierten quantenmechanischen Beschreibung des Komplexzentrums (Grundzustand plus angeregte Zustände) aus, in die das elektrostatische Ligandenfeld integriert wird. Das Ligandenfeld wird dabei durch empirisch bestimmbare Eigenschaften (Feldstärke) näher charakterisiert, was eine beliebig genaue Anpassung an die beobachtbare Wirklichkeit ermöglicht.

Kristallfeldtheorie

Die Kristallfeldtheorie, oft mit KFT oder CF-Theorie abgekürzt, entsprechend dem englischen Begriff Crystal Field Theory, wurde ab 1932 von John H. van Vleck – aufbauend auf einer Arbeit von Hans Bethe aus dem Jahre 1929 – entwickelt, um die physikalischen Eigenschaften von Übergangsmetallsalzen zu erklären, die unerwartetes magnetisches und optisches Verhalten zeigen.

Es handelt sich um ein rein elektrostatisches Modell, in dem die Anionen bzw. Liganden als negative Punktladungen betrachtet werden, deren elektrisches Feld, das Kristallfeld, die Elektronen der äußeren d-Orbitale der Kationen beeinflusst. Ein Kristall wird nicht als ganzes betrachtet, sondern es wird ein Kation herausgegriffen und nur der Einfluss der nächsten Nachbarn im Kristallgitter untersucht.

Prinzip des Kristallfeldes

Ausgangspunkt ist eine klassische Beschreibung des Ligandensystems, wobei die Liganden als negative Punktladungen betrachtet werden, deren elektrostatisches Feld, das Kristallfeld, die Elektronen der äußeren d-Orbitale des Komplexzentrums beeinflusst. Die Bezeichnung "Kristallfeld" drückt aus, dass bei der Wirkung der Liganden auf das Komplexzentrum entsprechend dem klassischen Verständnis eines Kristalls nur der Einfluss der nächsten Nachbarn untersucht wird.

Ligandenfeldtheorie

Die Ligandenfeldtheorie stammt von Hermann Hartmann und Friedrich Ernst Ilse und wurde 1951 veröffentlicht. Sie erlaubt eine sehr genaue Deutung der spektroskopischen Komplexeigenschaften.

Prinzip des Ligandenfeldes

Ausgangspunkt der Ligandenfeldtheorie ist das elektrostatische Ligandenpotential, das von Anfang an in die quantenmechanische Beschreibung integriert und durch empirisch-experimentell bestimmbare Größen wie Polarisierbarkeit und Feldstärke näher charakterisiert wird. Deshalb wird die Ligandenfeldtheorie auch als semi-empirische Theorie bezeichnet. Die Ligandenfeldtheorie ist aber keine MO-Theorie, weil nur die Valenzelektronen des Komplexzentrums quantenmechanisch behandelt werden und nicht auch das Elektronensystem der Liganden.[1]

Geometriebedingte Energieniveau-Aufspaltungen

Im freien Komplexzentrum sind die d-Orbitale entartet, d. h., sie besitzen die gleiche Energie. Bringt man ein Atom in ein kugelsymmetrisches Ligandenfeld, bleibt die Entartung erhalten, aber der Energieinhalt steigt aufgrund der repulsiven Wechselwirkung zwischen d-Elektronen und Liganden. In realen Komplexen ist das Ligandensystem nicht kugelsymmetrisch, sondern besitzt eine von den Größenverhältnissen zwischen Zentralatom und Liganden abhängige spezielle Geometrie. Als Folge davon destabilisieren die Liganden einige d-Orbitale stärker als die anderen und es kommt energetisch gesehen zu einer Aufspaltung der Zustände.

Die Art der Aufspaltung wird durch die Geometrie des Ligandensystems bestimmt. Die Kristallfeldtheorie liefert qualitative Abschätzungen in Form von Energieniveau-Diagrammen. Das ergibt die häufig zu findenden grafischen Darstellungen der Zustandsaufspaltung durch die Geometrie des Ligandensystems.

Die Ligandenfeldtheorie erlaubt es, die Größenordnung der Aufspaltung sehr genau und quantitativ zu berechnen. Die Größe der Aufspaltung hängt von der „Stärke“ des Zentralatoms und von der „Stärke“ der Liganden ab. Die Feldstärkeparameter der Komplexbestandteile werden empirisch bestimmt und relativ zueinander in Spektrochemische Reihen festgehalten.

Oktaedrische Komplexe

Darstellung der Betragsquadrate der D-Orbitale. Nähert man auf den Koordinatenachsen Liganden an, so steigt bei dem

d_{z^{2}}

und dem

d_{x^{2}-y^{2}}

Orbital die Energie.

Energieniveaudiagramm der d-Orbitale eines Komplexzentrums im oktaedrischen Feld

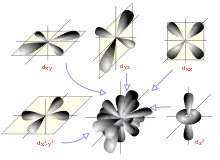
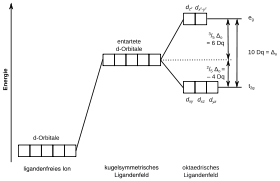
Sechs Punktladungen ordnen sich in Form eines Oktaeders um das Zentralatom an. Dadurch werden die Orbitale $d_{z^{2}}$ und $d_{x^{2}-y^{2}}$ energetisch angehoben, die Orbitale $d_{xy}$ , $d_{yz}$ und $d_{xz}$ energetisch abgesenkt. Es ergibt sich eine 2–3-Aufspaltung.

Ein Übergangsmetall-Zentralatom kann potentiell 3 × 2 = 6 Elektronen in den drei günstigen Orbitalen unterbringen, aber es muss Energie aufgewendet werden, damit sich zwei Elektronen in einem Orbital befinden können. Ob die günstigen Orbitale vollständig besetzt werden, hängt davon ab, ob dadurch mehr Energie gewonnen oder verloren wird, also davon, wie groß der Energieunterschied zwischen den Orbitalen ist.

So findet man bei schwachen Liganden high spin-konfigurierte Zentralatome, bei denen die energetisch niedriger gelegenen Orbitale nicht vollständig besetzt sind, und low spin-konfigurierte Komplexzentren mit vollständig besetzten Orbitalen bei vergleichsweise starken Liganden. Die beiden Elektronenanordnungen "high spin" und "low spin" gibt es beim oktaedrischen Kristallfeld nur bei d⁴, d⁵, d⁶, d⁷.

Sind in einem oktaedrischen Komplex Energieniveaus entartet, d. h., dass nicht festgestellt werden kann, in welchem Orbital sich ein Elektron befindet, tritt eine geometrische Verzerrung ein, solange bis diese Entartung aufgehoben ist. Dies wird als Jahn-Teller-Effekt bezeichnet.

Ein Beispiel stellt die d¹-Valenzelektronenkonfiguration dar: In einem oktaedrischen Feld muss dieses Elektron einem der drei t_2g Orbitale zugeschrieben werden. Da nicht bestimmbar ist, in welchem es sich tatsächlich befindet, kommt es zu einer Verzerrung, die einerseits dazu führt, dass nun genau gesagt werden kann, in welchem Orbital sich das Elektron befindet und andererseits eine Energieminimierung für dieses Elektron eintritt.

In diesem Beispiel (d¹) bewirkt die Jahn-Teller-Verzerrung eine Stauchung in z-Richtung. Daraus resultiert eine weitere Aufspaltung der t_2g- und e_g-Orbitale: Die Orbitale mit z-Anteil ( $d_{xz}$ , $d_{yz}$ , $d_{z^{2}}$ ) werden durch die Annäherung jener Liganden, die sich auf der z-Achse befinden, destabilisiert, wohingegen solche ohne z-Anteil $d_{x^{2}-y^{2}}$ , $d_{xy}$ ) weiter stabilisiert werden. In dieser neuen energetischen Orbitalabfolge kann das eine Elektron dem $d_{xy}$ -Orbital zugeschrieben werden, welches nun das stabilste (energetisch tiefstgelegene) Orbital darstellt. Da der Betrag der Stabilisierung und Destabilisierung gleich ist, liegt dieses $d_{xy}$ -Orbital nun tiefer, als vorher im „Verbund“ des entarteten t_2g-Satzes, was für das Elektron bedeutet, dass es im verzerrten (hier: gestauchten) Oktaeder eine größere Stabilisierung erfährt.

Ebenso ist in anderen Fällen eine Streckung entlang der z-Achse möglich, wodurch die Liganden auf dieser Achse weiter vom Zentralatom entfernt werden. Dies geht mit einer Stabilisierung aller Orbitale mit z-Komponente und folglich einer Destabilisierung aller Orbitale ohne z-Komponente einher.

Jahn-Teller-stabile Komplexe, also solche, die nicht der Jahn-Teller-Verzerrung unterliegen sind: d³, high-spin d⁵, low-spin d⁶, d⁸ und d¹⁰. In diesen sind die elektronischen Zustände nicht entartet.

Tetraedrische Komplexe

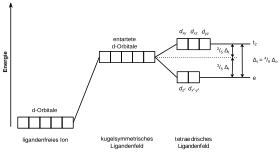
Energieniveaudiagramm der d-Orbitale eines Komplexzentrums im tetraedrischen Ligandenfeld

Vier Punktladungen können sich in Form eines Tetraeders um das zentrale Übergangsmetall anordnen. Durch diese Geometrie werden die Orbitale $d_{xy}$ , $d_{yz}$ und $d_{xz}$ energetisch angehoben und $d_{z^{2}}$ sowie $d_{x^{2}-y^{2}}$ energetisch abgesenkt. Das ergibt eine 3–2 Aufspaltung (t₂ und e).

Bei d³, d⁴, d⁵, d⁶ wären beide Konfigurationen "low spin" und "high spin" zu erwarten – wegen der geringen Feldaufspaltung existieren jedoch nur "high spin"-Komplexe (Eine Ausnahme stellt beispielsweise Tetrakis(1-norbornyl)cobalt(IV) dar, dessen Norbornyl-Liganden eine hinreichende Aufspaltung bewirken).

Die Ligandenfeldaufspaltung beim tetraedrischen Kristallfeld entspricht 4/9 der Oktaederaufspaltung.

Quadratisch-planare Komplexe

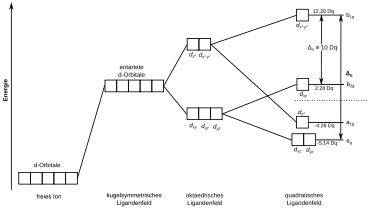
Energieniveaudiagramm der d-Orbitale eines Komplexzentrums im quadratisch-planaren Ligandenfeld, ausgehend vom oktaedrischen. Energieangaben in Dq sind für 3d-Übergangsmetalle. Das dz²-Orbital liegt im Regelfall energetisch höher als die beiden entarteten Orbitale.

Eine andere Möglichkeit für 4 Punktladungen ist das Quadrat. Die so entstehende Aufspaltung ist komplizierter: $d_{x^{2}-y^{2}}$ wird stark benachteiligt, leicht benachteiligt wird $d_{xy}$ , darunter liegen auf einer Stufe $d_{yz}$ und $d_{xz}$ , am tiefsten liegt $d_{z^{2}}$ (1-1-2-1 Aufspaltung).[2] (Je nach Metall kann sich die Reihenfolge der untersten beiden Niveaus jedoch umdrehen und das $d_{z^{2}}$ liegt über den $d_{yz}$ und $d_{xz}$ , z. B. bei Ni²⁺)

Diese Geometrie wird häufig bei d⁸-Konfigurationen (bzw. 16 Elektronen Komplexen) mit großer Ligandenfeldaufspaltung vorgefunden. Das $d_{x^{2}-y^{2}}$ -Orbital, das wegen elektrostatischer Abstoßung zu allen Liganden energetisch sehr hoch liegt, bleibt dabei unbesetzt.

Typisch ist diese Aufspaltung für Palladium-, Platin- und Gold-Kationen, da es bei ihnen meist zu der typischen großen Ligandenfeldaufspaltung kommt. Alle von diesen Ionen gebildeten Komplexe sind diamagnetische low-spin-Komplexe.

Andere Komplex-Geometrien

Die Kristall- und Ligandenfeldtheorien wurden auch erfolgreich zur Deutung des Effektes vieler anderer Komplex-Geometrien angewandt.

Metallocene: Metallocene haben die Aufspaltung 2-1-2. Die Orbitale in der xy-Ebene ( $d_{xy}$ und $d_{x^{2}-y^{2}}$ ) treten kaum in Wechselwirkung mit den Liganden und sind daher begünstigt. $d_{z^{2}}$ tritt nur mit einem Teil in Wechselwirkung und liegt in der Mitte. Stark destabilisiert werden $d_{xz}$ und $d_{yz}$ , die vollständig zu den Ringen zeigen.

Folgerungen aus der Energie-Aufspaltung

Farbe

Die Farben der Übergangsmetallsalze kommen durch die beschriebene Aufspaltung der d-Orbitale zustande. Elektronen aus den d-Orbitalen niedrigerer Energie können mit Licht in die Orbitale höherer Energie angeregt werden. Es wird nur Licht mit bestimmter Wellenlänge absorbiert, die genau der Energiedifferenz zwischen begünstigtem und benachteiligtem Orbital entspricht. Da die Abstände gering sind, liegt die Absorption im sichtbaren Bereich.

Besetzung der Orbitale zu High-Spin- oder Low-Spin-Komplexen

Es bestehen zwei Möglichkeiten, d-Orbitale zu besetzen:

Ist die Aufspaltung gering, so kann man die Orbitale als näherungsweise entartet betrachten. Die Besetzung erfolgt dann nach der Hundschen Regel, d. h., es wird zunächst jedes Orbital einfach besetzt und die ungepaarten Elektronen besitzen alle parallelen Spin. Weitere Elektronen müssen einen negativen Spin erhalten. Der Komplex hat daher einen hohen Nettospin und wird High-Spin-Komplex genannt.

Ist die Energieaufspaltung der Orbitale größer als die Spinpaarungsenergie, so gilt das Aufbauprinzip und es werden zunächst die energieärmeren Orbitale doppelt besetzt. Das resultiert im niederen Gesamtspin der Low-Spin-Komplexe.

Wenn ein Orbital mit zwei Elektronen gefüllt werden soll, muss eine Spinpaarungsenergie aufgewendet werden. Übersteigt die Ligandenfeldaufspaltung die Spinpaarungsenergie, kann es zum "Low-Spin-Komplex" kommen. D. h., tiefer liegende d-Orbitale werden zunächst mit zwei Elektronen gefüllt, bevor höher liegende d-Orbitale gefüllt werden.

Starke Liganden fördern die Ligandenfeldaufspaltung und somit die Bildung von Low-Spin-Komplexen (siehe dazu Spektrochemische Reihe). Zentralatome der 5. und 6. Periode neigen dank größerer Ligandenfeldaufspaltung zu Low-Spin-Komplexen. Je höher die Oxidationszahl der Zentralatome, desto stärker die Ligandenfeldaufspaltung und somit auch die Präferenz für Low-Spin-Komplexe.

Magnetismus

Je mehr ungepaarte Elektronen am Kation vorliegen, umso paramagnetischer ist es. Anhand der Aussagen zur Umbesetzung der d-Orbitale konnten die magnetischen Eigenschaften vieler Übergangsmetallsalze geklärt werden, vor allem erklärt die Formulierung von high spin- und low spin-konfigurierten Kationen den hohen Paramagnetismus von Eisen- oder Cobalt-Salzen mit schwachen Anionen/Liganden und den vergleichsweise niedrigen Paramagnetismus bei starken Anionen/Liganden. Sind alle Elektronen gepaart, dann ist das Ion diamagnetisch.

Thermodynamische Stabilität

Eine Verbindung ist thermodynamisch stabil, wenn sie selbst energetisch günstig ist und ein mögliches Produkt aus dieser Verbindung energetisch weniger günstig ist. Mit der Kristallfeldtheorie kann man anhand der d-Orbitalaufspaltung abschätzen, ob eine Verbindung günstiger oder nachteiliger als ihr Produkt ist und wie groß der energetische Unterschied dazwischen ist. Dadurch kann man vorhersagen, ob eine Reaktion thermodynamisch möglich ist. Diese Vorhersagen treffen auf den Großteil der ionischen und klassischen Komplexe zu.

Kinetische Inertheit

Eine Verbindung ist kinetisch inert, wenn die Reaktion zu einem Produkt zwar möglich, aber sehr langsam ist, d. h., wenn die Aktivierungsenergie für die Reaktion zum Produkt sehr hoch ist. Die Kristallfeldtheorie ermöglicht die Berechnung eines wesentlichen Anteils der Aktivierungsenergien für die Reaktionen von Übergangsmetallkomplexen durch die Betrachtung, wie die möglichen Übergangszustände oder Zwischenprodukte bei der Reaktion aussehen könnten und wie sich bei Bildung dieser Übergangszustände/Zwischenprodukte die d-Orbitalaufspaltung und Elektronenverteilung am Kation verändert. Sind die möglichen Übergangszustände energetisch sehr ungünstig gegenüber dem Ausgangszustand, ist die Aktivierungsenergie sehr hoch. Dementsprechend läuft die Reaktion fast gar nicht ab. Die Aussagen der Kristallfeldtheorie zur Kinetik von Ligandensubstitutionen an Komplexen sind sogar für nicht klassische Komplexe sehr zuverlässig.

Festkörperphysik

Die Ligandenfeldtheorie findet auch Anwendung in der Festkörperphysik zur Beschreibung von tiefen Störstellen in Halbleiter-Kristallen.

Gültigkeitsbereiche der Kristallfeld- und Ligandenfeldtheorie

Die Kristallfeldtheorie ist semi-klassisch und die Ligandenfeldtheorie semi-empirisch. Trotz der einschränkenden Voraussetzungen ist der Beitrag der Kristallfeldtheorie zum qualitativen Verständnis und der Beitrag der Ligandenfeldtheorie zur quantitativen Ableitung der Komplexeigenschaften groß. Der Grund dafür ist die quantenmechanische Behandlung des Komplexzentrums in beiden Theorien.

Die rein quantenmechanische MO-Theorie liefert zwar ein genaueres Bild der Komplexstruktur, weil auch die Liganden quantenmechanisch behandelt werden, doch ist das resultierende Aufspaltungsmuster dasselbe wie bei der Kristallfeld- und der Ligandenfeldtheorie. Was die Kristallfeld- bzw. Ligandenfeldtheorie als stärkere elektrostatische Abstoßung beschreibt, ist in der MO-Theorie größere Aufspaltung und Anhebung der antibindenden Orbitale (die bindenden werden von den Elektronen der Liganden besetzt). Nur die MO-Theorie liefert ein Verständnis des kovalenten Bindungsanteils bei Komplexen mit π-Rückbindung, wie sie z. B. in Carbonyl-Komplexen auftritt.

Die Valenz-Bindungs(VB)-Theorie von Linus Pauling liefert eine Erklärung für die von der Kristallfeld- und Ligandenfeldtheorie vorausgesetzte Komplexgeometrie.

Zum vollständigen Verständnis der Komplexverbindungen sind mehrere Theorien erforderlich.

Der systematische Zusammenhang zwischen allen Komplextheorien, insbesondere die Komplementarität von Kristallfeld- und Ligandenfeldtheorie, weist auf die Existenz eines einheitlichen Feldes molekularen Verhaltens, das eng mit der Raumstruktur verknüpft ist.

Literatur

A. F. Holleman, E. Wiberg, N. Wiberg: Lehrbuch der Anorganischen Chemie. 101. Auflage. Walter de Gruyter, Berlin 1995, ISBN 3-11-012641-9.
J. Huheey, E. Keiter, R. Keiter: Anorganische Chemie. WdeG, 2003
Erwin Riedel und andere: Moderne Anorganische Chemie. WdeG, 1999
Theodore L. Brown, H. Eugene LeMay, Bruce E. Bursten: "Chemie: Studieren kompakt" 10., aktualisierte Auflage, Pearson, 2011, ISBN 978-3-86894-122-7

Einzelnachweise

Erwin Riedel: Moderne Anorganische Chemie. WdeG, 1999, S. 237
E. Riedel: Moderne Anorganische Chemie. WdeG, 1999, S. 695

Siehe auch

Weblinks

Wikibooks: Ligandenfeldtheorie und die Vereinheitlichung molekularen Verhaltens – Lern- und Lehrmaterialien

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Erwin Riedel: Moderne Anorganische Chemie. WdeG, 1999, S. 237

[2] E. Riedel: Moderne Anorganische Chemie. WdeG, 1999, S. 695