BPP (Komplexitätsklasse)

In der Komplexitätstheorie steht BPP (engl. bounded error probabilistic polynomial time) für eine Komplexitätsklasse von Entscheidungsproblemen. Ein Problem liegt in BPP, wenn es einen polynomiell zeitbeschränkten probabilistischen Algorithmus gibt, der das Problem löst und dessen Fehlerwahrscheinlichkeit höchstens 1/3 beträgt. Die Verwendung einer beliebigen anderen konstanten Fehlerschranke kleiner als 1/2 ändert nichts an der Definition der Klasse BPP, durch mehrmalige Anwendung eines gegebenen BPP-Algorithmus lässt sich jede beliebige Fehlerschranke erreichen[1].

BPP-Algorithmen sind Monte-Carlo-Algorithmen, da sie mit einer geringen Wahrscheinlichkeit ein falsches Ergebnis liefern.

Definition

Eine Sprache ${\mathcal {L}}$ liegt genau dann in der Komplexitätsklasse ${\mathcal {BPP}}$ , wenn eine probabilistische Turing-Maschine $M$ existiert, für die gilt:[2]

$M$ läuft für alle Eingaben in polynomieller Zeit
$x\in {\mathcal {L}}\Rightarrow Pr[M(x)=1]\geq {\frac {2}{3}}$
$x\notin {\mathcal {L}}\Rightarrow Pr[M(x)=0]\geq {\frac {2}{3}}$

Die Konstante 2/3 ist willkürlich gewählt. Jede Konstante echt größer als 1/2 und sogar ${\frac {1}{2}}+|x|^{-c}$ für eine Konstante $c>0$ (wobei $|x|$ die Eingabelänge ist) führt zu einer äquivalenten Definition.[3]

Im Gegensatz zur Komplexitätsklasse ZPP wird hier gefordert, dass die Laufzeit der Turingmaschine $M$ für alle Eingaben polynomiell ist. Diese Forderung kann abgeschwächt werden, so dass wie bei ZPP nur noch gefordert wird, dass der Erwartungswert der Laufzeit durch ein Polynom beschränkt ist; die beiden Definitionen sind äquivalent.[4]

Eigenschaften

BPP ist abgeschlossen unter Komplementbildung, Vereinigung und Schnitt.[5] Das bedeutet, dass für zwei Sprachen $L_{1},L_{2}\in {\mathcal {BPP}}$ auch $L_{1}^{c},L_{1}\cup L_{2},L_{1}\cap L_{2}\in {\mathcal {BPP}}$ . Es ist also co-BPP = BPP.

Es ist kein BPP-vollständiges Problem bekannt und es gibt Hinweise darauf, dass es keine BPP-vollständigen Probleme gibt.[6]

Beziehung zu anderen Komplexitätsklassen

Inklusionen zwischen probabilistischen Komplexitätsklassen

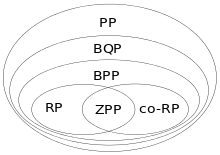
Die Klasse BPP liegt zwischen den Klassen RP und co-RP, bei denen nur einseitige Fehler erlaubt sind, und PP, bei der lediglich eine Fehlerschranke kleiner 1/2 gefordert wird, die auch von der Eingabelänge abhängen darf. Es gilt also (RP $\cup$ co-RP) ⊆ BPP ⊆ PP.[5] Es ist unbekannt, ob die Inklusionen echt sind, da P ⊆ RP und PP ⊆ PSPACE gilt.

Die Beziehung zur Klasse NP ist unbekannt, weder BPP ⊆ NP noch NP ⊆ BPP konnte bisher gezeigt werden, letzteres gilt aber als unwahrscheinlich. BPP liegt in der Polynomialzeithierarchie PH: ${\mathcal {BPP}}\subseteq \Sigma _{2}^{P}\cap \Pi _{2}^{P}.$ [7][8] Falls P = NP, kollabiert PH vollständig zu PH = P, in diesem Fall wäre BPP = P.

Die Klasse BQP ist das entsprechende Konzept zur Klasse BPP für Quantencomputer. Es gilt BPP ⊆ BQP.

Ein bedeutender Durchbruch in der Einschätzung von Zufallsalgorithmen gelang Avi Wigderson mit Russell Impagliazzo in den 1990er Jahren.[9] Sie zeigten, das unter bestimmten Bedingungen schnelle Zufallsalgorithmen immer in deterministische Algorithmen umgewandelt werden können (mit geeigneten Pseudozufallsgeneratoren): die Komplexitätsklasse BPP ist unter einer häufig als zutreffend angenommenen Voraussetzung gleich der Komplexitätsklasse P.[10] Die Voraussetzung ist, dass die Komplexitätsklasse E exponentielle Schaltkreiskomplexität hat.

Einzelnachweise

Christos H. Papadimitriou: Computational Complexity. Addison-Wesley, 1998, ISBN 0-201-53082-1, S. 259.
Sanjeev Arora und Boaz Barak: Computational Complexity: A Modern Approach. Cambridge University Press, 2009, ISBN 978-0-521-42426-4, S. 125.
Sanjeev Arora und Boaz Barak: Computational Complexity: A Modern Approach. Cambridge University Press, 2009, ISBN 978-0-521-42426-4, S. 132.
Sanjeev Arora und Boaz Barak: Computational Complexity: A Modern Approach. Cambridge University Press, 2009, ISBN 978-0-521-42426-4, S. 133.
Daniel Pierre Bovet und Pierluigi Crescenzi: Introduction to the Theory of Complexity. Prentice Hall, 1994, ISBN 0-13-915380-2, S. 195.
Daniel Pierre Bovet und Pierluigi Crescenzi: Introduction to the Theory of Complexity. Prentice Hall, 1994, ISBN 0-13-915380-2, S. 198,202.
Clemens Lautemann: BPP and the polynomial hierarchy. In: Information Processing Letters. Band 17, Nr. 4. Elsevier, 1983, S. 215–217, doi:10.1016/0020-0190(83)90044-3.
Johannes Köbler, Uwe Schöning, Jacobo Torán: The Graph Isomorphism Problem - It's Structural Complexity. Birkhäuser, 1993, ISBN 3-7643-3680-3, S. 78.
Kevin Hartnett, Pioneers Linking Math and Computer Science Win the Abel Prize, Quanta Magazine, 17. März 2021, anlässlich des Abelpreises 2021 zu einer Hälfte für Wigderson.
R. Impagliazzo, A. Wigderson: P=BPP if E requires exponential circuits: Derandomizing the XOR Lemma. In: 29th STOC, 1997, S. 220–229

Literatur

J. Gill. Computational complexity of probabilistic Turing machines, SIAM Journal on Computing 6(4):675-695, 1977.
Christos H. Papadimitriou: Computational Complexity. Addison-Wesley, Reading/Mass. 1995, ISBN 0-201-53082-1.

Weblinks

BPP. In: Complexity Zoo. (englisch)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Papa-1] Christos H. Papadimitriou: Computational Complexity. Addison-Wesley, 1998, ISBN 0-201-53082-1, S. 259.

[AB125-2] Sanjeev Arora und Boaz Barak: Computational Complexity: A Modern Approach. Cambridge University Press, 2009, ISBN 978-0-521-42426-4, S. 125.

[AB132-3] Sanjeev Arora und Boaz Barak: Computational Complexity: A Modern Approach. Cambridge University Press, 2009, ISBN 978-0-521-42426-4, S. 132.

[AB133-4] Sanjeev Arora und Boaz Barak: Computational Complexity: A Modern Approach. Cambridge University Press, 2009, ISBN 978-0-521-42426-4, S. 133.

[BoCr195-5] Daniel Pierre Bovet und Pierluigi Crescenzi: Introduction to the Theory of Complexity. Prentice Hall, 1994, ISBN 0-13-915380-2, S. 195.

[BoCr198-6] Daniel Pierre Bovet und Pierluigi Crescenzi: Introduction to the Theory of Complexity. Prentice Hall, 1994, ISBN 0-13-915380-2, S. 198,202.

[Lau83-7] Clemens Lautemann: BPP and the polynomial hierarchy. In: Information Processing Letters. Band 17, Nr. 4. Elsevier, 1983, S. 215–217, doi:10.1016/0020-0190(83)90044-3.

[KST78-8] Johannes Köbler, Uwe Schöning, Jacobo Torán: The Graph Isomorphism Problem - It's Structural Complexity. Birkhäuser, 1993, ISBN 3-7643-3680-3, S. 78.

[9] Kevin Hartnett, Pioneers Linking Math and Computer Science Win the Abel Prize, Quanta Magazine, 17. März 2021, anlässlich des Abelpreises 2021 zu einer Hälfte für Wigderson.

[10] R. Impagliazzo, A. Wigderson: P=BPP if E requires exponential circuits: Derandomizing the XOR Lemma. In: 29th STOC, 1997, S. 220–229