RP (Komplexitätsklasse)

RP (englisch randomized polynomial time, manchmal auch nur mit R bezeichnet) bezeichnet die Klasse der Entscheidungsprobleme, für die es einen randomisierten Algorithmus mit polynomieller Laufzeit gibt, der jede nicht zu akzeptierende Eingabe mit Wahrscheinlichkeit 1 ablehnt und für jede zu akzeptierende Eingabe eine Fehlerwahrscheinlichkeit von höchstens 1/2 hat. Die Verwendung einer beliebigen anderen konstanten Fehlerschranke kleiner als 1 ändert nichts an der Definition der Klasse RP, durch mehrmalige Anwendung eines gegebenen RP-Algorithmus lässt sich jede beliebige Fehlerschranke erreichen.

RP im Verhältnis zu anderen probabilistischen Komplexitätsklassen

Dieser Fehlertyp wird als einseitiger Fehler (one-sided error) bezeichnet, im Gegensatz zu dem zweiseitigen Fehler (two-sided error) bei der Komplexitätsklasse BPP.

Definition

Eine Sprache ${\mathcal {L}}$ liegt genau dann in der Komplexitätsklasse ${\mathcal {RP}}$ , wenn eine probabilistische Turingmaschine $M$ existiert, für die gilt:

$M$ läuft für alle Eingaben in polynomieller Zeit
$x\in {\mathcal {L}}\Rightarrow Pr[M(x)=1]\geq {\frac {1}{2}}$
$x\notin {\mathcal {L}}\Rightarrow Pr[M(x)=0]=1$

Die Konstante 1/2 ist willkürlich gewählt. Jede beliebige Konstante echt größer als 0 und weniger als 1 führt zu einer äquivalenten Definition.[1]

Im Gegensatz zur Komplexitätsklasse ZPP wird hier gefordert, dass die Laufzeit der Turingmaschine $M$ für alle Eingaben polynomiell ist. Diese Forderung kann abgeschwächt werden, so dass wie bei ZPP nur noch gefordert wird, dass der Erwartungswert der Laufzeit durch ein Polynom beschränkt ist; die beiden Definitionen sind äquivalent.[1]

Eigenschaften

RP ist abgeschlossen unter Vereinigung und Schnitt.[2] Das bedeutet, dass für zwei Sprachen $L_{1},L_{2}\in {\mathcal {RP}}$ auch $L_{1}\cup L_{2},L_{1}\cap L_{2}\in {\mathcal {RP}}$ . Es ist unbekannt, ob RP unter Komplementbildung abgeschlossen ist, die Komplementklasse von RP ist die Komplexitätsklasse co-RP.

Es ist kein RP-vollständiges Problem bekannt und es gibt Hinweise darauf, dass es keine RP-vollständigen Probleme gibt.[3]

Beziehung zu anderen Komplexitätsklassen

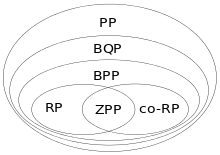
Sowohl RP als auch co-RP liegen zwischen den Klassen ZPP (= RP $\cap$ co-RP) und BPP, es gilt also ZPP ⊆ RP ⊆ BPP und ZPP ⊆ co-RP ⊆ BPP.[2]

Außerdem gilt RP ⊆ NP und co-RP ⊆ co-NP.[2]

Wenn NP ⊆ BPP, dann gilt sogar NP = RP.[4]

Einzelnachweise

Sanjeev Arora und Boaz Barak: Computational Complexity: A Modern Approach. Cambridge University Press, 2009, ISBN 978-0-521-42426-4, S. 133.
Daniel Pierre Bovet und Pierluigi Crescenzi: Introduction to the Theory of Complexity. Prentice Hall, 1994, ISBN 0-13-915380-2, S. 195.
Daniel Pierre Bovet und Pierluigi Crescenzi: Introduction to the Theory of Complexity. Prentice Hall, 1994, ISBN 0-13-915380-2, S. 198,202.
Johannes Köbler, Uwe Schöning, Jacobo Torán: The Graph Isomorphism Problem - It's Structural Complexity. Birkhäuser, 1993, ISBN 3-7643-3680-3, S. 73.

Literatur

Ingo Wegener: Komplexitätstheorie (S. 31–34) ISBN 3540001611
Köbler, Schöning, Toran: The Graph Isomorphism Problem - It's Structural Complexity (S. 68 ff.) - ISBN 3-7643-3680-3

Weblinks

RP. In: Complexity Zoo. (englisch)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[AB133-1] Sanjeev Arora und Boaz Barak: Computational Complexity: A Modern Approach. Cambridge University Press, 2009, ISBN 978-0-521-42426-4, S. 133.

[BoCr195-2] Daniel Pierre Bovet und Pierluigi Crescenzi: Introduction to the Theory of Complexity. Prentice Hall, 1994, ISBN 0-13-915380-2, S. 195.

[BoCr198-3] Daniel Pierre Bovet und Pierluigi Crescenzi: Introduction to the Theory of Complexity. Prentice Hall, 1994, ISBN 0-13-915380-2, S. 198,202.

[KST73-4] Johannes Köbler, Uwe Schöning, Jacobo Torán: The Graph Isomorphism Problem - It's Structural Complexity. Birkhäuser, 1993, ISBN 3-7643-3680-3, S. 73.