Knotentheorie
Die Knotentheorie ist ein Forschungsgebiet der Topologie. Sie beschäftigt sich unter anderem damit, die topologischen Eigenschaften von Knoten zu untersuchen. Eine Fragestellung ist etwa, ob zwei gegebene Knoten äquivalent sind, also ob sie ineinander überführt werden können, ohne dass dabei die Schnur „zerschnitten“ wird. Die Knotentheorie beschäftigt sich im Gegensatz zur Knotenkunde nicht mit dem Knüpfen von Knoten in der Praxis, sondern mit mathematischen Eigenschaften von Knoten.

Mathematische Definition
Man nehme ein verknotetes Stück Schnur und verklebe die beiden Enden; in der Fachsprache heißt das Ergebnis eine Einbettung der Kreislinie in den dreidimensionalen Raum. Zwei Knoten gelten als gleich, wenn sie durch eine stetige Verformung ineinander überführt werden können (Isotopie).
In der Knotentheorie werden auch Einbettungen von mehreren Kreislinien untersucht; diese nennt man Verschlingungen (Links). Eine andere Erweiterung des Themas sind mehrdimensionale Knoten, das heißt Einbettungen der Sphären der Dimension in den -dimensionalen Raum für .
Eine dreidimensionale geschlossene glatte Kurve, die nicht verknotet ist und damit isotop zur Kreislinie, heißt Unknoten oder trivialer Knoten.
Technische Details: zahme Knoten und ambiente Isotopie
Streng genommen muss die obige Definition an zwei Stellen nachgebessert werden, um dem herkömmlichen Knotenbegriff zu entsprechen, denn:
- Sie lässt wilde Knoten zu, d. h. unendlich viele Knoten in einem (endlichen) Stück Schnur.
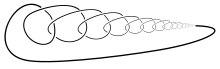 Ein wilder Knoten
Ein wilder Knoten - Mit einer gewöhnlichen Isotopie kann man einen Knoten so stramm ziehen, dass er verschwindet.[1]
Es gibt zwei Wege, diese Probleme zu beheben:
- Man ersetzt Isotopie durch ambiente Isotopie und beschränkt sich auf zahme Knoten: Bei einer ambienten Isotopie muss auch der Raum um den Knoten sich stetig deformieren; ein Knoten heißt zahm, falls er zu einem stückweise linearen Knoten ambient isotop ist.[2]
- Man beschränkt sich auf glatte Isotopien zwischen glatten Knoten, denn jeder stetig differenzierbare Knoten ist zahm,[3] und jede glatte Isotopie lässt sich zu einer ambienten Isotopie fortsetzen.[4]
Beide Lösungen sind äquivalent.[5] Im Weiteren gelten alle Knoten als zahm.
Knotendiagramme und Reidemeister-Bewegungen
In der Knotentheorie wird ein Knoten oft durch seine Projektion auf eine Ebene dargestellt. Jeder (zahme) Knoten hat eine reguläre Projektion, d. h. eine Projektion mit nur endlich vielen Doppelpunkten (Kreuzungen)[6].
Um aus einer Projektion den Knoten rekonstruieren zu können, muss man bei jeder Kreuzung angeben, welcher der beiden Stränge oben bzw. unten liegt. Eine Projektion mit dieser Zusatzinformation nennt man ein Knotendiagramm. Jeder zahme Knoten lässt sich somit durch ein Diagramm darstellen. Ein solches Diagramm ist jedoch nicht eindeutig, denn jeder Knoten lässt sich durch unendlich viele verschiedene Diagramme darstellen. Zum Beispiel ändern die folgenden lokalen Züge zwar das Diagramm, nicht aber den dargestellten Knoten:
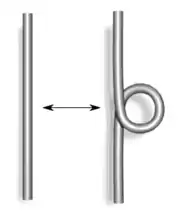 ; ; |  ; ; | 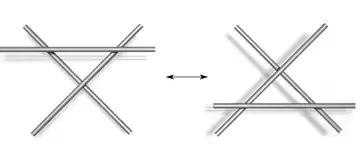 . . |
| Typ I | Typ II | Typ III |
Diese Züge werden Reidemeister-Bewegungen genannt, zu Ehren von Kurt Reidemeister. Dieser hat 1927 gezeigt, dass diese drei Züge bereits ausreichen: Zwei Knotendiagramme stellen genau dann den gleichen Knoten dar, wenn sie durch eine endliche Folge von Reidemeister-Bewegungen ineinander überführt werden können.
Knoteninvarianten
Zwei Knoten können sehr unterschiedlich aussehen und trotzdem im obigen Sinne gleich sein. Folglich kann es schwierig sein, direkt nachzuweisen, dass zwei Knoten nicht gleich sind. Daher wählt man einen indirekten Weg: Knoteninvarianten.[7]
Eine Knoteninvariante ordnet jedem Knoten eine Zahl (oder ein Polynom oder eine Gruppe usw.) zu, und zwar so, dass der Wert sich nicht ändert, wenn man den Knoten im dreidimensionalen Raum stetig deformiert. Anders gesagt: Man ordnet jedem Knotendiagramm einen Wert zu, und zwar so, dass die Reidemeister-Züge den Wert nicht ändern. Beispiele:
- Die Kreuzungszahl[8] eines Knotens ist die kleinstmögliche Anzahl von Kreuzungen, die in irgendeinem Knotendiagramm von vorkommt. Dass die Kreuzungszahl eine Invariante ist, geht bereits aus ihrer Definition hervor; aber die Berechnung ist im Allgemeinen sehr schwer. Für einen alternierenden Knoten realisiert das reduzierte Diagramm die Kreuzungszahl.
- Alexander-Polynom, die erste Polynominvariante von Knoten, eingeführt 1923 von James Alexander
- HOMFLY-Polynom
- Die Dreifärbungszahl[9]: Ein Knotendiagramm besteht aus Bögen und Kreuzungen; an jeder Kreuzung treffen sich drei Bögen. Bei einer Dreifärbung ordnet man jedem Bogen eine der Farben rot, blau oder grün zu, und zwar so, dass an jeder Kreuzung die drei Bögen entweder drei verschiedene Farben oder dreimal die gleiche Farbe haben. Die Dreifärbungszahl ist die Anzahl der Dreifärbungen. Mit der Dreifärbungszahl weist man nach, dass der Kleeblattknoten verknotet ist und dass die Borromäischen Ringe tatsächlich verlinkt sind.
- Das Jones-Polynom ordnet jedem Knoten ein Laurent-Polynom zu. Das Jones-Polynom kann man mit Hilfe von Knotendiagrammen algorithmisch berechnen, indem man für alle Kreuzungen geeignete Terme zu einem Gesamtpolynom addiert. Zur Invarianz genügt es zu zeigen, dass das so konstruierte Polynom invariant unter den drei Reidemeister-Bewegungen ist. Das Jones-Polynom kann den Kleeblatt-Knoten von seinem Spiegelbild unterscheiden. Nach Edward Witten kann es über Observable (Wilson-Loops) einer dreidimensionalen topologischen Quantenfeldtheorie dargestellt werden, der Chern-Simons-Theorie. Diese Quantenfeldtheorie ist gleichzeitig eine Eichfeldtheorie, und je nach Wahl der Eichgruppe erhält man verschiedene Knoteninvarianten (Alexander-Polynom, HOMEFLY-Polynom, Jones-Polynom u. a.).
- Durch Kategorifizierung des Jones-Polynoms führte Mikhail Khovanov Ende der 1990er Jahre als neue Knoteninvariante die Khovanov-Homologie von Links ein. Das Jones-Polynom, HOMEFLY-Polynom und Alexander-Polynom sind Eulercharakteristiken von speziellen Homologien innerhalb der Khovanov-Homologie. Eine Interpretation als topologische Quantenfeldtheorie – diesmal eine supersymmetrische Eichfeldtheorie in vier Dimensionen – mit der Khovanov-Homologie als Observablen gab Edward Witten.[10] Catharina Stroppel gab eine darstellungstheoretische Interpretation der Khovanov-Homologie durch Kategorifizierung von Quantengruppen-Invarianten. Die Khovanov-Homologie hat auch Verbindungen zur Floer-Homologien.
- Das System der Wassiljew-Invarianten,[11] eine Reihe unendlich vieler Knoteninvarianten, die um 1990 von Wiktor Anatoljewitsch Wassiljew (Vassiliev) eingeführt wurden. Während in der üblichen Knotentheorie eine Einbettung der Kreislinie in den betrachtet wird – ohne singuläre Punkte – betrachtete Wassiljew die Diskriminante, das heißt das Komplement zum Raum der Knoten im Raum aller Abbildungen von der Kreislinie in den . Er betrachtete also die Erweiterung auf singuläre Knoten, was eine unendliche Reihe von Stufen ergibt (nicht singulär, ein Doppelpunkt, zwei Doppelpunkte usw.) Die Wassiljew-Invarianten enthalten die meisten vorher bekannten polynomialen Invarianten. Es ist ein offenes Problem, ob sie vollständig sind, das heißt, die Knoten eindeutig charakterisieren. Maxim Kontsevich gab eine kombinatorische Interpretation der Wassiljew-Invarianten. Sie können auch störungstheoretisch über Chern-Simons-Theorien berechnet werden.
Bis heute ist noch keine einfach berechenbare Knoteninvariante gefunden worden, die alle nicht-äquivalenten Knoten unterscheidet, also für zwei Knoten genau dann identisch ist, wenn diese äquivalent sind. Eine solche zu finden, ist ein wichtiges Ziel der aktuellen Forschung. Es ist auch unbekannt, ob das Jones-Polynom den trivialen Knoten erkennt, also ob es einen nicht-trivialen Knoten gibt, dessen Jones-Polynom gleich dem des trivialen Knoten ist.
Typen von Knoten
- chirale und amphichirale Knoten
- Primknoten und zusammengesetzte Knoten
- Bandknoten: Rand einer Scheibe, deren Selbstschnitte nur aus Bandsingularitäten bestehen
- Scheibenknoten: Rand einer glatten Scheibe im Halbraum
- Brezelknoten: aus Tangles zusammengesetzter Knoten
- 2-Brücken-Knoten: Knoten der Brückenzahl
- Torusknoten: Knoten, der auf einem unverknoteten Torus gezeichnet werden kann
- Satellitenknoten: Knoten, der auf einem verknoteten Torus gezeichnet werden kann
- hyperbolische Knoten: Knoten, dessen Komplement eine hyperbolische Mannigfaltigkeit ist
Anwendungen
Lange Zeit war die Beschäftigung mit Knoten eher von rein theoretischem Interesse. Mittlerweile existieren aber eine Reihe wichtiger Anwendungen, etwa in der Biochemie bzw. Strukturbiologie, mit denen überprüft werden kann, ob komplizierte Faltungen von Proteinen mit anderen Proteinen übereinstimmen. Ähnliches gilt für DNA. Weitere aktuelle Anwendungen gibt es in der Polymerphysik. Eine wichtige Stellung nimmt die Knotentheorie in der modernen theoretischen Physik ein, wo es etwa um Pfade in Feynmandiagrammen geht.
Die Knotentheorie wird auch in benachbarten Gebieten der Topologie und Geometrie genutzt. Zur Untersuchung 3-dimensionaler Räume sind Knoten sehr nützlich, da sich jede orientierbare geschlossene 3-dimensionale Mannigfaltigkeit durch Dehn-Chirurgie an einem Knoten oder einer Verschlingung erzeugen lässt. In der hyperbolischen Geometrie spielen Knoten eine Rolle, weil die Komplemente der meisten Knoten in der 3-dimensionalen Sphäre eine vollständige hyperbolische Metrik tragen.
Literatur
- Colin C. Adams: The Knot Book. An elementary introduction to the mathematical theory of knots. 1994; 2004, ISBN 0-8218-3678-1
- Das Knotenbuch. Einführung in die mathematische Theorie der Knoten. Spektrum, Heidelberg/Berlin/Oxford 1995, ISBN 3-86025-338-7
- Meike Akveld: Knoten in der Mathematik. Ein Spiel mit Schnüren, Bildern und Formeln. Orell Fuessli, Zürich 2007, ISBN 978-3-280-04050-8
- Gerhard Burde, Heiner Zieschang: Knots. de Gruyter, Berlin / New York 1985, ISBN 3-11-008675-1
- Gunnar Hornig: Magnetes Geheimnis. In: RUBIN – Das Wissenschaftsmagazin der Ruhr-Universität Bochum. 2/01, S. 6–10, ruhr-uni-bochum.de (PDF)
- Louis H. Kauffman: Knots and Physics. World Scientific, 1991, ISBN 981-02-0343-8
- Knoten. Diagramme, Zustandsmodelle, Polynominvarianten. Spektrum, Heidelberg/Berlin/Oxford 1995, ISBN 3-86025-232-1
- Charles Livingston: Knotentheorie für Einsteiger, Vieweg, 1995, ISBN 3-528-06660-1
- Lee Neuwirth: Knotentheorie. In: Spektrum der Wissenschaft. August 1979, ISSN 0170-2971 (unter anderem: Modell eines mathematischen Knotens, Beziehungen zwischen Geometrie und Algebra)
- Dale Rolfsen: Knots and Links. AMS Chelsea Publ., 2003, ISBN 0-8218-3436-3
- Alexei Sossinsky: Nœuds. Genèse d’une théorie mathématique. Éditions du Seuil, Paris 1999, ISBN 2-02-032089-4 (Science Ouverte).
- Mathematik der Knoten. Rowohlt-Taschenbuch-Verlag, Reinbek 2000, ISBN 3-499-60930-4
Weblinks
- Robert G. Scharein: The KnotPlot Site. (Software für interaktives Visualisieren, Manipulieren und Simulieren von mathematischen Knoten)
- C. Livingston, A. H. Moore: KnotInfo: Table of Knot Invariants
- Alexander Stoimenow: Knot data tables
- Marc Lackenby: Elementary Knot Theory (irreführender Titel, es handelt sich um eine Einführung in die aktuelle Forschung)
Einzelnachweise
- Gerhard Burde, Heiner Zieschang: Knots. 2. Auflage. de Gruyter, Berlin 2003, ISBN 3-11-017005-1, S. 2.
- Gerhard Burde, Heiner Zieschang: Knots. 2. Auflage. de Gruyter, Berlin 2003, ISBN 3-11-017005-1, S. 2–3.
- Richard H. Crowell, Ralph H. Fox: Introduction to Knot Theory. Springer, New York, ISBN 0-387-90272-4, S. 5 (Aussage 2.1).
- Florian Deloup: The fundamental group of the circle is trivial. In: The American Mathematical Monthly. Band 112, Nr. 5, Mai 2005, S. 417–425, doi:10.2307/30037492 (Theorem 5).
- Victor V. Prasolov, Alexei B. Sossinsky: Knots, Links, Braids and 3-Manifolds (= Translations of Mathematical Monographs. Band 154). American Mathematical Society, Providence, RI 1997, ISBN 0-8218-0588-6, S. 8 (§1.3).
- Richard H. Crowell, Ralph H. Fox: Introduction to Knot Theory. Springer, New York, ISBN 0-387-90272-4, S. 7 (Aussage 3.1).
- Knot Invariant, ncatlab
- Charles Livingston: Knotentheorie für Einsteiger. Vieweg, Braunschweig/Wiesbaden 1995, ISBN 3-528-06660-1, S. 116.
- Charles Livingston: Knotentheorie für Einsteiger. Vieweg, Braunschweig/Wiesbaden 1995, ISBN 3-528-06660-1 (Abschnitte 3.2 und 3.3).
- Khovanov Homology, ncatlab
- Vassiliev Invariant, Mathworld