Hyperbolische Geometrie

Die hyperbolische Geometrie (auch Lobatschewskische Geometrie oder Lobatschewski-Geometrie genannt) ist ein Beispiel für eine nichteuklidische Geometrie, das man erhält, wenn man zu den Axiomen der absoluten Geometrie anstelle des Parallelenaxioms, das die euklidischen Geometrien kennzeichnet, das diesem widersprechende hyperbolische Axiom[1] hinzunimmt. Dieses besagt, dass es zu einer Geraden g und einem Punkt P (der nicht auf g liegt) nicht wie in der euklidischen Geometrie nur genau eine, sondern mindestens zwei Geraden (h und i) gibt, die durch P gehen und zu g parallel sind. Dass zwei Geraden „parallel“ zueinander sind, bedeutet hier aber lediglich, dass sie in derselben Ebene liegen und keine gemeinsamen Punkte haben, nicht dass sie überall den gleichen Abstand haben (h und i haben nur einen gemeinsamen Punkt P).

Modell einer Parkettierung einer Ebene mit Quadraten. An den Ecken treffen dabei mehr als vier zusammen (je nach Größe, hier fünf).

Es lässt sich zeigen, dass es dann zu einer beliebigen Geraden g durch jeden Punkt außerhalb von g unendlich viele Nichtschneidende („Parallelen“) gibt, die in der durch den Punkt und die Gerade bestimmten Ebene liegen.[1] Zwei davon sind in einer Grenzlage und heißen grenzparallel (auch: horoparallel) zur Geraden, während die restlichen Geraden überparallel (auch: hyperparallel) genannt werden.

Darstellungen der reellen hyperbolischen Ebene

Es gibt verschiedene Arten, wie die reelle hyperbolische Ebene in der reellen euklidischen Ebene dargestellt werden kann. Die meisten davon lassen sich für höhere Dimensionen verallgemeinern.

Auf jede dieser Arten wird die gleiche abstrakte hyperbolische Geometrie dargestellt: Die reelle hyperbolische Ebene. Es ist daher möglich, zwischen diesen Darstellungen umzurechnen und Aussagen in rein hyperbolischer Geometrie sind vom verwendeten „Modell“ unabhängig. Gewöhnlich spricht man in der Mathematik dann von unterschiedlichen Modellen, wenn zwei nicht isomorphe Strukturen das gleiche Axiomensystem erfüllen. Insofern beschreiben die folgenden „Modelle“ die gleiche Struktur, sind also nur verschiedene Darstellungen eines Modells. Diese Darstellungen werden jedoch in der Literatur immer als Modelle bezeichnet, so auch hier. Zu hyperbolischen Ebenen über anderen Körpern und mehr als zweidimensionalen hyperbolischen Räumen siehe Metrische absolute Geometrie.

Kreisscheibenmodell von Beltrami und Klein

In dieser von Eugenio Beltrami und Felix Klein entwickelten Darstellung gilt:

Die hyperbolische Ebene wird durch eine offene Kreisscheibe modelliert.
Hyperbolische Geraden werden durch Sehnen modelliert.
Längen werden durch eine spezielle Distanzfunktion definiert (auch die Winkel sind verschieden von den euklidischen Werten).

Diese Darstellung ist auch unter dem Namen „Bierdeckelgeometrie“ bekannt.[2]

Distanzfunktion

Abstand zweier Punkte in einer hyperbolischen Geometrie

Sind A und B zwei Punkte der Kreisscheibe, so trifft die durch A und B verlaufende Sehne den Kreis in zwei Punkten R und S. Der hyperbolische Abstand von A und B wird nun mit Hilfe des Doppelverhältnisses $(A,B,R,S)$ definiert:

d(A,B)={\frac {1}{2}}\ln(A,B,R,S)={\frac {1}{2}}\ln {\frac {{\overline {RB}}\cdot {\overline {SA}}}{{\overline {RA}}\cdot {\overline {SB}}}}

.

Poincarésches Kreisscheibenmodell

Bei dem auf Beltrami zurückgehenden Kreisscheibenmodell von Henri Poincaré gilt:

Die hyperbolische Ebene wird durch eine offene Kreisscheibe (meist den Einheitskreis) modelliert.
Hyperbolische Geraden werden durch Kreisbögen (und Durchmesser), die auf dem Rand senkrecht stehen, modelliert.
Die hyperbolische Winkelmessung entspricht der euklidischen Winkelmessung, wobei der Winkel zwischen zwei Kreisbögen über deren Tangenten am Schnittpunkt bestimmt wird.
Die hyperbolische Längenmessung erfolgt durch eine spezielle Distanzfunktion.

Distanzfunktion

Seien $A$ und $B$ zwei Punkte der Kreisscheibe. Fasst man die Ebene als komplexe Zahlenebene auf, so entsprechen den Punkten $A$ , $B$ komplexe Zahlen $a$ , $b$ . Der hyperbolische Abstand von $A$ und $B$ wird nun mit Hilfe dieser komplexen Zahlen definiert:

d(A,B)=\operatorname {arcosh} \left(1+{\frac {2\cdot \left\|a-b\right\|^{2}}{\left(1-\left\|a\right\|^{2}\right)\cdot \left(1-\left\|b\right\|^{2}\right)}}\right)

Poincarésches Halbebenenmodell

Bei dem auf Beltrami zurückgehenden Halbebenenmodell von Henri Poincaré gilt:

Die hyperbolische Ebene wird durch die obere Halbebene (y>0) modelliert.
Hyperbolische Geraden werden durch Kreisbögen (und Halbgeraden) modelliert, die auf der x-Achse senkrecht stehen.
Die hyperbolische Winkelmessung entspricht der euklidischen Winkelmessung, wobei der Winkel zwischen zwei Kreisbögen über deren Tangenten am Schnittpunkt bestimmt wird.

Distanzfunktion

Der Abstand zwischen zwei Punkten der oberen Halbebene wird mit der folgenden Formel berechnet:

\operatorname {d} (\langle x_{1},y_{1}\rangle ,\langle x_{2},y_{2}\rangle )=\operatorname {arcosh} \left(1+{\frac {{(x_{2}-x_{1})}^{2}+{(y_{2}-y_{1})}^{2}}{2y_{1}y_{2}}}\right)\,.

Hyperboloid-Modell

Das auf Poincaré zurückgehende Hyperboloidmodell bettet die hyperbolische Ebene in den dreidimensionalen Minkowskiraum ein.

Erlanger Programm

Im Sinne von Felix Kleins Erlanger Programm ist hyperbolische Geometrie die Geometrie von

(O(n,1),O(n)\times O(1))

.

Das Beltrami-Klein-Modell zeigt, dass man hyperbolische Geometrie als Teil der projektiven Geometrie auffassen kann.

Dreieck

Dreieck im hyperbolischen Raum

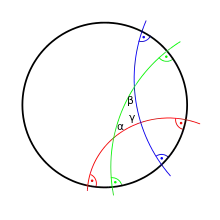
In der reellen hyperbolischen Geometrie ist die Winkelsumme in einem Dreieck immer kleiner als π (180 Grad; bzw. zwei Rechte, wenn man das Winkelmaß vermeiden will). Für sehr große Dreiecke kann sie beliebig klein werden. Die Fläche des Dreiecks wird nach Johann Heinrich Lamberts Formel berechnet:

\pi -(\alpha +\beta +\gamma )=C\,\Delta ,

wobei α, β und γ die jeweiligen Winkel, Δ die Fläche und die Konstante C ein Skalierungsfaktor ist. Der Skalierungsfaktor C ist abhängig vom verwendeten Einheitensystem und im Grunde gleich 1 zu setzen. Ist der Faktor C negativ, spricht man von einer (positiven) Gaußschen Krümmung. Analog dazu definierte Thomas Harriot zuvor im Jahr 1603 die Formel

\Delta =R^{2}\,(\alpha +\beta +\gamma -\pi )

für die Fläche eines Dreiecks auf einer Kugeloberfläche, das von Kreisen mit demselben Radius wie die Kugel gebildet wird. Hierbei gilt der Zusammenhang

C=-{\frac {1}{R^{2}}}

.

Da für die hyperbolische Geometrie ein positiver Wert für C erforderlich ist, muss es sich bei R aufgrund von

R=(-C)^{-{\frac {1}{2}}}

um einen imaginären Radius handeln.

Siehe auch

Literatur

Geschichte

Jeremy Gray: Ideas of Space: Euclidean, Non-Euclidean, and Relativistic. 2. Auflage. Oxford University Press, Oxford 1989, ISBN 0-19-853935-5.
Marvin Jay Greenberg: Euclidean & Non-Euclidean Geometries: Development and History. W. H. Freeman, 1993, ISBN 0-7167-2446-4.
David Hilbert: Grundlagen der Geometrie. 14. Auflage. Teubner, Stuttgart/Leipzig 1999, ISBN 3-519-00237-X (Online-Kopie der Ausgabe von 1903 [abgerufen am 28. Juni 2013]).
Nikolai I. Lobachevsky: Pangeometry, Edited and translated by Athanase Papadopoulos, Heritage of European Mathematics. Vol. 4, European Mathematical Society (EMS), Zürich, ISBN 978-3-03719-087-6.

Die Hyperbolische Geometrie im Rahmen der Differentialgeometrie (Geometrien auf Flächen)

Norbert A'Campo, Athanase Papadopoulos: Notes on hyperbolic geometry. In: Strasbourg Master class on Geometry. European Mathematical Society (EMS), Zürich, ISBN 978-3-03719-105-7, S. 1–182, doi:10.4171/105. (IRMA Lectures in Mathematics and Theoretical Physics, Vol. 18)
Athanase Papadopoulos (Hrsg.): Handbook of Teichmüller theory. Vol. I, European Mathematical Society (EMS), Zürich 2007, ISBN 978-3-03719-029-6, doi:10.4171/029. (IRMA Lectures in Mathematics and Theoretical Physics 11)
Athanase Papadopoulos (Hrsg.): Handbook of Teichmüller theory. Vol. II, European Mathematical Society (EMS), Zürich 2009, ISBN 978-3-03719-055-5, doi:10.4171/055. (IRMA Lectures in Mathematics and Theoretical Physics 13)
Athanase Papadopoulos (Hrsg.): Handbook of Teichmüller theory. Vol. III, European Mathematical Society (EMS), Zürich 2012, ISBN 978-3-03719-103-3, doi:10.4171/103. (IRMA Lectures in Mathematics and Theoretical Physics 19)

Die (reelle) hyperbolische Ebene als Modell einer absoluten Geometrie im Hilbertschen Sinn

Friedrich Bachmann: Aufbau der Geometrie aus dem Spiegelungsbegriff. 2. ergänzte Auflage. Springer, Berlin/Heidelberg/New York 1973, ISBN 3-540-06136-3, V: Hyperbolische Geometrie und §20.13:Hilbert-Ebenen (Definiert Absolute Geometrie sehr allgemein, erläutert vor diesem Hintergrund die Besonderheiten der reellen hyperbolischen Geometrie).
Benno Klotzek: Euklidische und nichteuklidische Elementargeometrien. 1. Auflage. Harri Deutsch, Frankfurt am Main 2001, ISBN 3-8171-1583-0 (Elementar heißt hier nicht einfach: Lösung von Konstruktionsaufgaben und Koordinatisierungen der „klassischen“ nichteuklidischen Geometrien).

Einzelnachweise

Klotzek (2001), 2.1
Susanne Müller-Philipp, Hans-Joachim Gorski: Leitfaden Geometrie: Für Studierende der Lehrämter. Vieweg+Teubner Verlag, 5. erweiterte Auflage, 2012, ISBN 978-3-8348-1234-6, S. 71 (Auszug (Google))

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Klotzek-1] Klotzek (2001), 2.1

[2] Susanne Müller-Philipp, Hans-Joachim Gorski: Leitfaden Geometrie: Für Studierende der Lehrämter. Vieweg+Teubner Verlag, 5. erweiterte Auflage, 2012, ISBN 978-3-8348-1234-6, S. 71 (Auszug (Google))