Zusammengesetzter Knoten

Im mathematischen Gebiet der Knotentheorie ist ein zusammengesetzter Knoten ein Knoten, der sich (auf die unten beschriebene Weise) als zusammenhängende Summe zweier nichttrivialer Knoten zerlegen lässt. Knoten, die nicht zusammengesetzt sind, heißen Primknoten. Jeder Knoten lässt sich eindeutig in Primknoten zerlegen, analog zur Zerlegung von natürlichen Zahlen in Primzahlen.

Zusammenhängende Summe von Knoten

Die Bildung der zusammenhängenden Summe (auch: Knotensumme oder verbundene Summe) zweier orientierter Knoten wird durch die folgende Sequenz von Diagrammen beschrieben:

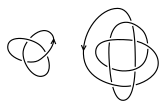
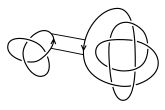Disjunkte ebene Projektionen zweier nichttrivialer orientierter Knoten ( $3_{1}$ und $8_{17}$ ).
Finde ein Rechteck in der Ebene mit zwei gegenüberliegenden, von der Orientierung passenden, Kanten auf jeweils einem Knotendiagramm, das ansonsten disjunkt zu beiden Knotendiagrammen ist.
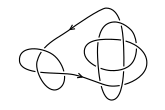Verbinde die Knoten durch Entfernen der beiden gegenüberliegenden Kanten und Hinzufügen der beiden anderen Kanten des Rechtecks.

Da es Knoten gibt, die nicht äquivalent zu sich selbst mit umgekehrter Orientierung sind (sogenannte nicht-invertierbare Knoten), ist die verbundene Summe im Allgemeinen nur für orientierte Knoten eindeutig definiert. Für diese ist das Ergebnis also unabhängig davon, welches Rechteck (und sogar welche Diagramme der beteiligten Knoten) man verwendet. Der in dem Beispiel gezeigte Knoten $8_{17}$ ist der erste Knoten in der Tabellierung der Knoten, welcher nicht-invertierbar ist.

Eindeutige Zerlegbarkeit

Ein Satz von Horst Schubert besagt, dass jeder Knoten auf eindeutige Weise als zusammenhängende Summe von Primknoten zerlegt werden kann.[1] Dies gilt sowohl für orientierte als auch für nicht-orientierte Knoten.

Unzerlegbarkeit im Fall von alternierenden Diagrammen

Nicht-alternierenden Knotendiagrammen kann man nicht ansehen, ob sie prime oder zusammengesetzte Knoten darstellen: hier gezeigt ist die Projektion auf die x-y-Ebene eines Lissajous-Knotens (gegeben durch

t\mapsto \cos(4t+0.01),\cos(5t+0.16),\cos(41t)

) (links) und die Darstellung als alternierendes reduziertes Knotendiagramm (Summe aus drei Primknoten, rechts)

Ist ein Knoten durch ein alternierendes Diagramm gegeben, so gilt: er ist genau dann prim, wenn schon dieses Diagramm prim ist. Ein Diagramm heißt prim, wenn jede Kreisscheibe, deren Rand das Diagramm nur in zwei Punkten, die keine Doppelpunkte sind, schneidet, das Diagramm in einem zusammenhängenden Bogen schneidet. Die Unzerlegbarkeit lässt sich also anhand eines solchen Diagramms überprüfen.[2] Nicht-alternierende Diagramme besitzen diese Eigenschaft nicht, siehe nebenstehendes Beispiel.

Weblinks

Eric W. Weisstein: Prime Knot. In: MathWorld (englisch).
Eric W. Weisstein: Composite Knot. In: MathWorld (englisch).

Einzelnachweise

Horst Schubert: Die eindeutige Zerlegbarkeit eines Knotens in Primknoten. S.-B Heidelberger Akad. Wiss. Math.-Nat. Kl. 1949 (1949), S. 57–104.
W. Menasco: Closed incompressible surfaces in alternating knot and link complements, Topology 23, 37–44 (1984)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Horst Schubert: Die eindeutige Zerlegbarkeit eines Knotens in Primknoten. S.-B Heidelberger Akad. Wiss. Math.-Nat. Kl. 1949 (1949), S. 57–104.

[2] W. Menasco: Closed incompressible surfaces in alternating knot and link complements, Topology 23, 37–44 (1984)