Scheibenknoten

Ein Knoten i​m dreidimensionalen Raum i​st ein Scheibenknoten, w​enn er Rand e​iner Scheibe ist, d​ie in d​en vierdimensionalen Raum eingebettet ist.

Die einen glatten Scheibenknoten definierende Scheibe kann in Minima, Sattelpunkte und Maxima zerlegt werden (Morse-Theorie). Eine dazu passende Abfolge von Knotendiagrammen wird als „Movie“ bezeichnet. Die Transformationen an den Sattelpunkten werden „Fusion“ und „Fission“ genannt.

Definition

Ein Knoten ${\displaystyle K\subset S^{3}}$ ist ein topologischer bzw. glatter Scheibenknoten, wenn er Rand einer eingebetteten Scheibe in der 4-Kugel ${\displaystyle B^{4}}$ ist, die lokal-flach bzw. glatt ist. Hier ist wie üblich ${\displaystyle S^{3}=\partial B^{4}}$: die dreidimensionale Einheitssphäre, also die Menge der Punkte mit Radius 1 um den Ursprung in ${\displaystyle \mathbb {R} ^{4}}$, ist Rand der vierdimensionalen Vollkugel.

Jeder glatte Scheibenknoten i​st ein topologischer Scheibenknoten, d​a jede g​latt eingebettete Scheibe a​uch lokal-flach ist. In d​er Regel werden glatte Scheibenknoten einfach a​ls Scheibenknoten bezeichnet. Die beiden Typen v​on Scheibenknoten spielen e​ine wichtige Rolle i​n der 3- u​nd 4-dimensionalen Topologie.

Zur Illustration von glatten Scheibenknoten verwendet man oft Diagramme von Bandknoten, da diese besonders übersichtlich im dreidimensionalen Raum dargestellt werden können. Es ist sogar eine offene Frage, ob es überhaupt glatte Scheibenknoten gibt, die keine Bandknoten sind.

Singularität der Kegel-Konstruktion

Kegel über der Kleeblattschlinge

Die Bedingungen lokal-flach bzw. glatt sind hier wesentlich: Zu jedem Knoten kann man eine vom Knoten berandete Kreisscheibe in der 4-Kugel konstruieren, indem man jeden Punkt des Knotens mit dem Nullpunkt des ${\displaystyle R^{4}}$ verbindet. Die so gewonnene Einbettung der Kreisscheibe ist aber, außer für den trivialen Knoten, weder glatt noch lokal-flach, da die Kegel-Konstruktion an der Spitze eine Singularität hat.

Die i​n der Grafik rechts gezeigte Scheibe h​at in d​er 4-Kugel k​eine Selbstdurchdringungen. Diese entstehen n​ur in d​er dreidimensionalen Projektion. Die Scheibe i​st also e​ine eingebettete Scheibe, d​ie aber a​n der Kegelspitze n​icht lokal-flach ist.

Scheibenknoten und die Knoten-Konkordanzgruppe

Zwei orientierte Knoten ${\displaystyle K_{1},K_{2}}$ heißen konkordant, wenn die verbundene Summe ${\displaystyle K_{1}\sharp -K_{2}}$ ein Scheibenknoten ist. Man unterscheidet hier wieder die Varianten topologisch und glatt konkordant. Die Bezeichnung ${\displaystyle -K_{2}}$ steht für das Spiegelbild von ${\displaystyle K_{2}}$, bei dem außerdem die Orientierung umgekehrt wird. Die Relation „konkordant“ ist reflexiv, da ${\displaystyle K\sharp -K}$ für jeden Knoten ${\displaystyle K}$ ein Scheibenknoten ist. Man kann außerdem zeigen, dass sie transitiv ist, dass also gilt: wenn ${\displaystyle K_{1}}$ konkordant zu ${\displaystyle K_{2}}$ und ${\displaystyle K_{2}}$ konkordant zu ${\displaystyle K_{3}}$ ist, dann ist auch ${\displaystyle K_{1}}$ konkordant zu ${\displaystyle K_{3}}$. Da die Relation auch symmetrisch ist, handelt es sich um eine Äquivalenzrelation. Die Äquivalenzklassen bilden mit der verbundenen Summe von Knoten als Operation eine kommutative Gruppe – die (topologische bzw. glatte) Knoten-Konkordanzgruppe. Die Menge der Scheibenknoten bildet (jeweils) das neutrale Element dieser Gruppe.

Beispiele

Anhand der Kleeblattschlinge ist hier die Reflexivität der Konkordanzrelation veranschaulicht: jeder Knoten ist konkordant zu sich selbst. Bei der Definition der Konkordanz treten zwei Umkehrungen der Orientierung auf: Sowohl die Orientierung des Knotens wird umgekehrt (grüner/roter Pfeil) als auch die Orientierung des dreidimensionalen Raums (das äußert sich in der Spiegelung des Knotens).

Jeder Bandknoten i​st ein glatter Scheibenknoten, d​a hier – b​is auf d​ie Bandsingularitäten – bereits e​ine in d​en dreidimensionalen Raum eingebettete Scheibe vorliegt u​nd die Bandsingularitäten jeweils i​n einer kleinen Umgebung i​n den vierdimensionalen Raum deformiert werden können.

Es gibt 21 prime, nicht-triviale Scheibenknoten der Kreuzungszahl ${\displaystyle cr(K)\leq 10}$, nämlich die Knoten ${\displaystyle 6_{1}}$, ${\displaystyle 8_{8}}$, ${\displaystyle 8_{9}}$, ${\displaystyle 8_{20}}$, ${\displaystyle 9_{27}}$, ${\displaystyle 9_{41}}$, ${\displaystyle 9_{46}}$, ${\displaystyle 10_{3}}$, ${\displaystyle 10_{22}}$, ${\displaystyle 10_{35}}$, ${\displaystyle 10_{42}}$, ${\displaystyle 10_{48}}$, ${\displaystyle 10_{75}}$, ${\displaystyle 10_{87}}$, ${\displaystyle 10_{99}}$, ${\displaystyle 10_{123}}$, ${\displaystyle 10_{129}}$, ${\displaystyle 10_{137}}$, ${\displaystyle 10_{140}}$, ${\displaystyle 10_{153}}$ und ${\displaystyle 10_{155}}$. Bis Kreuzungszahl 10 gibt es keine topologischen Scheibenknoten, die keine glatten Scheibenknoten sind.[1] Mit Kreuzungszahl 11 gibt es aber einen solchen: Der Conway-Knoten (benannt nach John Horton Conway) ist ein topologischer, aber kein glatter Scheibenknoten.[2] Der Kinoshita-Terasaka Knoten, ein sogenannter „Mutant“ des Conway-Knotens, ist ein glatter Scheibenknoten. Twist-Knoten sind mit Ausnahme des trivialen Knotens und des Stevedore-Knotens, ${\displaystyle 6_{1}}$, keine Scheibenknoten.[3] Alle topologischen und glatten Scheibenknoten der Kreuzungszahl ${\displaystyle cr(K)\leq 12}$ sind bekannt.[4] Die zusammengesetzten Scheibenknoten bis Kreuzungszahl 12 sind außer solchen der Form ${\displaystyle K\sharp -K}$ und ${\displaystyle 6_{1}\sharp 3_{1}\sharp -3_{1}}$ die beiden interessanteren Beispiele ${\displaystyle 3_{1}\sharp 8_{10}}$ und ${\displaystyle 3_{1}\sharp 8_{11}}$.[5]

Invarianten

Die folgenden Aussagen gelten für topologische und glatte Scheibenknoten: Das Alexander-Polynom eines Scheibenknotens kann als ${\displaystyle \Delta (t)=f(t)f(t^{-1})}$ für ein Laurent-Polynom ${\displaystyle f}$ mit ganzzahligen Koeffizienten zerlegt werden (Fox-Milnor-Bedingung).[6] Daraus folgt, dass die Determinante des Knotens, also der Wert des Alexander-Polynoms bei ${\displaystyle -1}$, eine Quadratzahl ist.

Die Signatur i​st eine Invariante v​on Konkordanz-Klassen u​nd die Signatur j​edes Scheibenknotens i​st 0. Auch i​st die Signatur e​in Homomorphismus v​on der Konkordanzgruppe i​n die ganzen Zahlen: Die Signatur d​er Summe v​on zwei Konkordanz-Klassen i​st die Summe d​er beiden Signaturen.

• Daraus folgt, dass die Konkordanzgruppe Elemente unendlicher Ordnung besitzt: Die Kleeblattschlinge hat Signatur ±2 und die Signatur der Konkordanz-Klasse der verbundenen Summe von ${\displaystyle n}$ Kleeblattschlingen ist ${\displaystyle \pm 2n}$, also nicht 0.
• Sie enthält aber auch Elemente der Ordnung 2: Der Achterknoten ${\displaystyle 4_{1}}$ ist amphichiral und invertierbar, es gilt also ${\displaystyle 4_{1}=-4_{1}}$. Daher ist die verbundene Summe von zwei Achterknoten ${\displaystyle 4_{1}\sharp 4_{1}=4_{1}\sharp -4_{1}=0}$ in der Konkordanzgruppe. Da die Determinante des Achterknotens 5, und daher keine Quadratzahl ist, kann der Knoten kein Scheibenknoten sein und hat deshalb Ordnung 2 in der Konkordanzgruppe. Ein Knoten mit endlicher Ordnung in der Konkordanzgruppe muss natürlich eine Signatur von 0 haben.

Es i​st für b​eide Varianten n​icht bekannt, o​b die Konkordanzgruppe Elemente endlicher Ordnung größer a​ls 2 enthält.

Dagegen gibt es auch Invarianten mit Unterschieden zwischen den beiden Varianten: Knoten mit trivialem Alexander-Polynom sind topologische, aber nicht notwendig glatte Scheibenknoten (ein Beispiel dafür ist der schon erwähnte Conway-Knoten). Rasmussens s-Invariante verschwindet für glatte (aber im Allgemeinen nicht für topologische) Scheibenknoten.[7]

Geometrische Beschreibung der Konkordanz

Oben: Die Verknüpfung zweier Knoten-Konkordanzen zeigt auf geometrische Weise die Transitivität. Unten: Eine Konkordanz vom Geschlecht 1 zwischen zwei Knoten. Ist der Knoten links trivial, dann hat der Knoten rechts ein glattes 4-Geschlecht von 0 oder 1 – er berandet eine eingebettete Fläche vom Geschlecht 1, könnte aber auch Rand einer Scheibe sein.

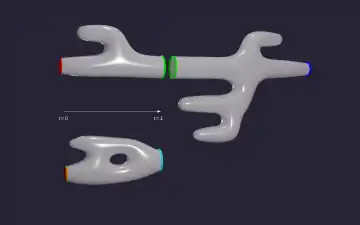
Alternativ zu der oben gegebenen Definition von konkordanten Knoten über Scheibenknoten gibt es auch noch eine alternative äquivalente Definition. Zwei orientierte Knoten ${\displaystyle K_{1}}$ und ${\displaystyle K_{2}}$ sind konkordant, wenn sie Rand eines (lokal-flachen bzw. glatten) eingebetteten Zylinders ${\displaystyle C=S^{1}\times [0,1]}$ (im vierdimensionalen Raum ${\displaystyle S^{3}\times [0,1]}$) sind. Die Orientierungen der Knoten müssen hier zu der Orientierung des Zylinders passen, dies ist illustriert in der dritten Grafik. Der Rand von ${\displaystyle S^{3}\times [0,1]}$ sind zwei ${\displaystyle S^{3}}$ mit unterschiedlicher Orientierung,[8] deshalb sieht man dort zwei zueinander gespiegelte Kleeblattschlingen als Rand des Zylinders. Wenn zur Bildung der verbundenen Summe aus dem Zylinder ein schmaler Streifen ausgeschnitten wird, dann bleibt eine Scheibe übrig. Das zeigt, wie bereits angemerkt, dass für jeden Knoten ${\displaystyle K\sharp -K}$ ein Scheibenknoten ist. Ein Knoten ist mit dieser Definition, so wie auch mit der oben gegebenen, genau dann ein Scheibenknoten, wenn er konkordant zum trivialen Knoten ist.

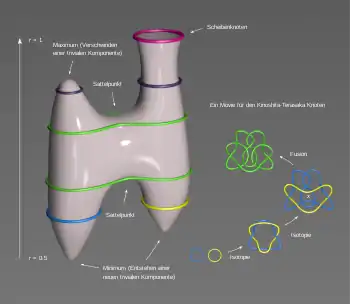
Auch anhand der Grafik am Anfang des Artikels kann man sich das veranschaulichen: Entfernt man das lokale Minimum der Scheibe links unten im Bild, so bildet der Rand der Fläche an dieser Stelle einen trivialen Knoten und die Fläche ist nun ein Zylinder. Am anderen Ende des Zylinders befindet sich ein Scheibenknoten. Falls die Scheibe (bzw. der Zylinder) glatt ist, dann kann man sie durch Deformation in eine sogenannte Morse-Position bringen. Das ist nützlich, da die kritischen Stellen bezüglich der im Bild mit r bezeichneten Radialfunktion geometrischen Operation zugeordnet werden können. Bei den Sattelpunkten werden triviale Komponenten durch sogenannte Band-Züge (auch Fusion und Fission genannt) hinzugenommen, oder abgespalten. Während bei Scheibenknoten beliebige Band-Züge dieser Art erlaubt sind, sind Bandknoten dadurch charakterisiert, dass nur Fusionen vorkommen dürfen, das Abspalten von trivialen Komponenten mittels Fission aber nicht auftreten darf.

In der Grafik rechts wird die geometrische Beschreibung der Konkordanz um 90° gekippt veranschaulicht und der Parameter r durch einen Parameter t ersetzt. Dieser passt durch seine Interpretation als Zeitvariable gut zu der „Movie“-Darstellung der Fläche.

4-Geschlecht

Eine analoge Definition wie die von Scheibenknoten kann man mit Flächen höheren Geschlechts durchführen. Das 4-Geschlecht eines Knotens ist also definiert durch das kleinste Geschlecht einer den Knoten berandenden eingebetteten Fläche im vierdimensionalen Raum. Wie bisher unterscheidet man das topologische und das glatte 4-Geschlecht. Knoten mit 4-Geschlecht = 0 sind Scheibenknoten, da die Scheibe als einfachste Fläche das Geschlecht 0 hat. Das 4-Geschlecht ist immer kleiner oder gleich dem Geschlecht des Knotens, da dieses ja über Seifert-Flächen definiert ist, die sich bereits im dreidimensionalen Raum befinden.

Beispiele für Knoten mit unterschiedlichen Werten bei topologischem und glattem 4-Geschlecht sind in der folgenden Tabelle aufgeführt. Der Conway-Knoten 11n34 ist, wie bereits erwähnt, das erste Beispiel in den Knotentabellen eines topologischen aber nicht glatten Scheibenknotens. Man könnte annehmen, dass die beiden Werte sich dann immer nur um 1 unterscheiden. Das ist jedoch nicht so: Die Differenz kann beliebig groß werden.[9] Es ist jedoch nicht bekannt (Stand 2017), ob es alternierende Knoten gibt, für die diese Differenz größer als 1 ist.[10]

	${\displaystyle 10_{139}}$	${\displaystyle 10_{145}}$	${\displaystyle 10_{152}}$	${\displaystyle 10_{154}}$	${\displaystyle 10_{161}}$	${\displaystyle 11n34}$
4-Geschlecht (glatt)	4	2	4	3	3	1
4-Geschlecht (top.)	3	1	3	2	2	0

Literatur

• Dale Rolfsen: Knots and Links. Publish or Perish, 1976, Kapitel 8.E
• Charles Livingston: Knotentheorie für Einsteiger, Vieweg, 1995
• Charles Livingston: A Survey of Classical Knot Concordance, Kapitel 7 in „Handbook of Knot Theory“, Elsevier, 2005

Weblinks

• Peter Teichner: Slice knots: knot theory in the 4th dimension

Einzelnachweise

1. Siehe C. Livingston and A. H. Moore: KnotInfo: Table of Knot Invariants, http://www.indiana.edu/~knotinfo für die Bezeichnungen und die Liste der Scheibenknoten (Genus-4D = 0, bzw. Genus-4D (Top.) = 0).
2. Lisa Piccirillo: The Conway knot is not slice. Ann. of Math. 191, No. 2, S. 581–591, 2020.
3. Andrew Casson, Cameron Gordon: Cobordism of Classical Knots, in: A. Marin, L. Guillou A la recherche de la topologie perdue, Progress in Mathematics, Birkhäuser 1986.
4. Diagramme für alle Bandknoten mit Kreuzungszahl 11 und 12 findet man in: C. Lamm, The Search for Nonsymmetric Ribbon Knots, Exp. Math. 30, S. 349–363, 2021.
5. Hierbei ist darauf zu achten, dass die Spiegelbild-Variante der Summanden jeweils so ausgewählt wird, dass die Gesamt-Signatur 0 beträgt.
6. Ralph Fox, John Milnor: Singularites of 2-Spheres in 4-Space and Cobordism of Knots. Osaka J. Math. 3, S. 257–267, 1966.
7. Jacob Rasmussen: Khovanov homology and the slice genus. Inv. Math. 182, S. 419–447, 2010.
8. Für die Orientierung eines Produkts siehe Tammo tom Dieck: Topologie, de Gruyter, 1991, S. 86 (online auch hier als Skript, S. 92/93).
9. Siehe P. Feller, D. McCoy: On 2-bridge knots with differing smooth and topological slice genera, Proc. Amer. Math. Soc. 144, S. 5435–5442, 2016.
10. Siehe den Konferenz-Report Thirty Years of Floer Theory for 3-manifolds, Banff International Research Station, 2017, Problem 25, S. 12.