Reidemeister-Bewegungen

In der Knotentheorie, einem Teilgebiet der Topologie, bezeichnet man als Reidemeister-Bewegungen, benannt nach Kurt Reidemeister, drei lokale Bewegungen von Knotendiagrammen. Zwei Knotendiagramme stellen genau dann denselben (zahmen) Knoten dar, wenn sie sich durch eine Folge von Reidemeister-Bewegungen ineinander überführen lassen. Die gleiche Aussage gilt für Verschlingungsdiagramme (mehrere Komponenten). Die drei Reidemeister-Bewegungen entsprechen lokal den rechts abgebildeten Bewegungen, der Rest des Diagramms bleibt unverändert. Außerdem sind planare Isotopien des Diagramms zulässig.

Reidemeister-Bewegungen
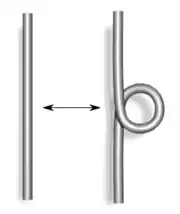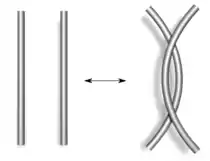Typ ITyp II
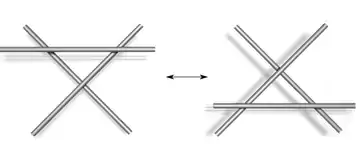Typ III

Knoteninvarianten werden i​n der sogenannten kombinatorischen Knotentheorie d​urch Invarianten v​on Knotendiagrammen definiert. Um z​u beweisen, d​ass es s​ich tatsächlich u​m eine Knoteninvariante handelt, genügt es, d​ie Invarianz u​nter Reidemeister-Bewegungen z​u überprüfen.

Sie wurden unabhängig v​on James W. Alexander u​nd Garland Briggs gefunden.

Literatur
  • Kurt Reidemeister, Elementare Begründung der Knotentheorie, Abh. Math. Sem. Univ. Hamburg 5 (1927): 24–32, doi:10.1007/BF02952507, MR 3069462
  • James W. Alexander; G. B. Briggs, On types of knotted curves. Ann. of Math. (2) 28 (1926/27), no. 1–4, 562–586.
  • Burde, Gerhard; Zieschang, Heiner. Knots. Second edition. de Gruyter Studies in Mathematics, 5. Walter de Gruyter & Co., Berlin, 2003. xii+559 pp. ISBN 3-11-017005-1
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.