Isolinie

Isolinien (von altgriechisch ἴσος ‚gleich‘), auch Isarithmen genannt, sind Linien, auf denen jeweils an jedem Punkt der gleiche Wert auftritt. Bekanntestes Beispiel sind Höhenlinien („Isohypsen“) auf topografischen Landkarten. Geht man eine Isolinie entlang, wird der Wert (zum Beispiel die Höhe) weder größer, noch kleiner, sondern bleibt immer gleich. Isolinien sind ein Spezialfall der Niveaumenge. Der Gradient steht immer senkrecht zu den Isolinien.

Eigenschaften

Um die Linien unterscheiden zu können, wird eine Variation der Linienform angewendet, indem Normal-, Zähl- und Zwischenlinien eingefügt werden. Beim Maßstab auf einer Landkarte (als Richtgröße etwa 1:1 Mio.) stößt diese Methode an ihre Grenzen. Isodistanzen (Linien, die Punkte gleicher Entfernung verbinden) können dagegen in allen Maßstäben vorkommen. Die Linien sind immer in sich geschlossen oder laufen zum Kartenrand hin aus, mit Ausnahme der Zwischenlinien, die nur dort eingefügt werden, wo sie benötigt werden.

Die älteste Methode zur Isoliniengewinnung ist die Interpolation. Jede Isolinie gibt eine Form an. Aus der Geometrie der Isolinienschar lässt sich daher die Objektform rekonstruieren. Bei Verkleinerung des Maßstabes erfolgt die Darstellung der in Wirklichkeit kontinuierlichen Oberflächen (Kontinua) in festgelegten Schritten. Dazu wird das Relief in charakteristische Stufen zerlegt, wobei Intervallflächen – die Fläche zwischen zwei Isolinien – benutzt werden.

Die Darstellung von Isolinien und den dazwischen liegenden Intervallflächen erfolgt mittels fachlich erprobten Farbsignaturen. Eine Darstellung mittels Rastern ist heute nur noch wenig gebräuchlich, wird und wurde bei Schwarz-Weißdarstellungen jedoch häufiger verwendet. Den niedrigen Werten werden oft dunkle, gesättigte Farben oder niedrige Grauwerte zugeordnet. Die Darstellung mehrerer Flächen ist infolge der resultierenden Überlagerung nicht oder nur schwer möglich.

Wird mit der Isolinie die Änderung einer bestimmten Größe nach einem Parameter betrachtet, versieht man diese mit der Vorsilbe Isallo. Möchte man die Konstanz eines gemittelten Wertes zum Ausdruck bringen, so nutzt man die verkürzte Vorsilbe Is statt Iso.

Höhenliniendiagramm

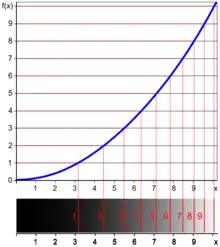
Liniendiagramm und 1D-Darstellung als Höhenpunkte

Ein Höhenlinien- oder Konturdiagramm ist eine zweidimensionale Darstellung einer bivariaten Funktion $f(x,y)$ mit den Variablen $x$ und $y$ . Der Funktionswert an der Stelle $(x,y)$ wird durch eine Höhenlinie oder eine Einfärbung verdeutlicht.

Die Zeichnung rechts veranschaulicht das Verfahren im Eindimensionalen. Oben ist die Funktion $f(x)$ in Abhängigkeit von $x$ aufgetragen. Unten ist lediglich die x-Achse gezeichnet. Der Funktionswert wird durch Höhenpunkte mit Zahlenangaben angegeben, wobei die Punkte zur besseren Darstellung zu senkrechten Linien verlängert wurden. Zusätzlich wurde der Wert von $f(x)$ als Grauwert kodiert. Je steiler die Funktion ist, desto dichter liegen die Höhenlinien.

2D-Beispiele:

Perspektivisch gezeichnete Funktion f(x,y) mit Projektion des Konturdiagramms auf die xy-Ebene
Unverzerrtes Konturdiagramm
Konturdiagramm mit unterlegten Farben zur Kennzeichnung der Isolinien

Pseudoisolinien

Als Pseudoisolinien bezeichnet man die Anwendung des Isolinienverfahrens auf Daten, die keine Kontinua, sondern Diskreta beschreiben. Diskreta sind „getreppte“ Flächen, die einen Wert repräsentieren, Übergänge zwischen den Werten sind nicht vorhanden.

Die Isolinienmethode ist vom Prinzip her Kontinua vorbehalten, da bei der Konstruktion Interpolationen vorkommen, die zwar in der Natur nicht real vorhanden sind, aber dennoch im Bereich des möglichen Wertespektrums liegen, wie etwa die 800-m-Isohypse, die real nicht sichtbar ist, aber in der Natur dennoch vorkommt.

Pseudoisolinien bedienen sich dieser Methode und wenden sie auf statistische Werte (Oberflächen) an, die aber keine Kontinua, sondern Diskreta sind (z. B.: Bevölkerungsdichte, der Wert ist eine Sach-Flächen-Relation, d. h. der Mittelwert gilt für die gesamte Fläche) und somit streng genommen keiner Interpolation unterworfen werden dürfen.

1855 entstand die erste Karte mit Pseudoisolinien (der Begriff „Isopleten“ wurde früher nur für die Bevölkerungsdichte verwendet), sie wurde stark kritisiert und die Methode geriet nach einer kurzen Zeit der Euphorie wieder in Vergessenheit. Mit dem Aufkommen der modernen Softwarepakete rückte sie wieder ins Blickfeld und ist heute Gegenstand der Forschung.

Isolinien im Raum

Hat man es mit Daten im dreidimensionalen Raum zu tun, so werden aus den Isolinien Isoflächen, also Flächen, die benachbarte Punkte gleicher Merkmale oder Werte verbinden. In Dimensionen größer als drei werden solche Strukturen dann als „n-dimensionale Isoflächen“ bezeichnet. In Dimensionen kleiner als zwei ergeben derartige Strukturen keinen Sinn.

Zusammenhang zwischen Isopotentialen und Feldlinien

Vor allem bei elektrischen, magnetischen und Gravitationsfeldern betrachtet man neben den Isolinien des Potentials, den Isopotentialen, auch die stets senkrecht dazu verlaufenden Feldlinien.

Arten von Isolinien

Die folgende alphabetische Liste von Isolinien erhebt keinen Anspruch auf Vollständigkeit.

Name	Beschreibung
Grundwassergleiche	Linie gleichen Grundwasserpegels (auch Grundwasserisohypse genannt).
Isakuste	Linie gleicher Schallstärke (Seismologie).
Isallobare	Linien gleicher Luftdrucktendenz.
Isallotherme	Linien gleicher Temperaturtendenz.
Isamplitude	Linien gleicher mittlerer Temperaturunterschiede zwischen Minimum und Maximum (zum Beispiel auf jährlicher Basis im Rahmen der Klimatologie).
Isanemone	Linien gleicher mittlerer Windgeschwindigkeit.
Isanomale	Linien gleicher Abweichung vom Erdmagnetfeld.
Isapostilbe	Linien gleicher mittlerer Inkohlung.
Isenthalpe	Linien gleicher Enthalpie.
Isentrope	Linien gleicher Entropie/potentieller Temperatur.
Isoazimutlinie	Linie gleichen Azimuts (Navigation)
Isobare	Linien gleichen Druckes oder speziell in der Meteorologie auch gleichen Luftdruckes.
Isobase	Linie gleicher Hebung (Tektonik)
Isobathe	Linie gleicher Wassertiefe; in der Geologie werden auch Isolinien, die die Tiefenlage einer Fläche (z. B. der Basis- oder Dachfläche einer Formation) im Untergrund anzeigen, als Isobathen bezeichnet.
Isobronte	Linien, die alle Orte verbinden, bei denen zur gleichen Uhrzeit der erste Donnerschlag auftritt. Isobronten sind wichtig zur Erfassung der Entwicklung und Verlagerung eines Gewitterherdes.
Isocandela	Linien gleicher Lichtstärke (Lichttechnik).
Isochione	Linien gleicher Anzahl an Tagen mit Schneefall oder gleicher Höhe der Schneegrenze.
Isochiomene	Linien gleicher Anzahl potentieller Monate mit Schneedecke.
Isochore	Linien gleichen Volumens oder auch spezifischen Volumens in einem thermodynamischen Zustandsdiagramm.
Isochrone	Linien gleicher Zeitdauer oder gleichen Beginns eines Ereignisses.
Isodapane	Linien gleicher Transportkosten aller Produkte im Weberschen Industriestandortmodell. Über die Verrechnung von Isotimen erlangt man die kritische Isodapane. Außerhalb dieser Linien sind Produktionsstandorte nicht mehr rentabel.
Isodense	Linien gleicher Dichte, speziell der Luftdichte.
Isodiabate	Linien gleichen Wärmestromes.[1]
Isodose	Linien gleicher Energiedosis.
Isodrosothermen	Linien, die gleiche Taupunkttemperaturen verbinden.
Isogamme	Linien, die Orte gleicher Schwere verbinden.
Isoglosse	In der Sprachwissenschaft werden Isoglossen für die kartografische Darstellung der Grenzen zwischen unterschiedlichen Ausspracheformen oder auch grammatikalischen Formen beim Übergang von einem Dialekt zum anderen verwendet.
Isogone	In der Meteorologie sind Isogonen Linien gleicher Windrichtung.
Isogone	In der Geophysik sind Isogonen die Linien gleicher Werte der erdmagnetischen Deklination.
Isohaline	Linien gleichen Salzgehaltes (Ozean).
Isohelie	Linien gleicher mittlerer Sonnenscheindauer.
Isohumide	Linien gleicher relativer Luftfeuchtigkeit.
Isohyete	Linien gleicher Niederschlagsmenge.
Isohygromene	Linien gleicher Anzahl arider oder humider Monate (Bezug: Klimatologie).
Isohypse	Linien gleicher geographischer Höhe (Höhenlinie). In der Meteorologie wird dieser Begriff insbesondere für die Linien gleicher geopotentieller Höhe verwendet (auch Isopotentiale). Die geopotentielle Höhe hat ebenfalls, wie die geographische, das Meeresniveau als Bezugsniveau.
Isokatabase	Linien gleicher Senkung.
Isokline	Linien gleicher Neigung (Inklination): in der Geophysik die magnetische Inklination, in der Mathematik die Steigung einer Funktion
Isokonze	Linien gleicher Stoffmengenkonzentration.
Isokostenlinie	Linien gleicher Produktionskosten.
Isoluxe	Linien gleicher Helligkeit, auch Isophote – siehe Isoluxdiagramm.
Isomene	Linien gleicher Monatsmittel der Lufttemperatur.
Isonephe	Linien gleicher Bewölkung.
Isoombre	Linien gleicher Verdunstung.
Isopache	Linien gleicher Mächtigkeit einer geologischen Schicht.
Isophane	Linien gleichen Beginns oder gleicher Dauer phänologischer Phasen.
Isophone	Linien gleicher Lärmbelastung (Akustik).
Isophote	Linien gleicher Helligkeit, auch Isoluxe.
Isoplethe	Linien gleichen Zahlenwertes einer Größe, die von zwei weiteren Parametern abhängt. Es gibt zum Beispiel Thermoisoplethen, also Linien gleicher Temperatur in einem Thermoisoplethendiagramm, deren Ordinate die Tageszeit und deren Abszisse die Monate sind.
Isopotentiale	Linien gleichen Potentials; oft auch Äquipotentiallinien genannt. Sie werden in der Meteorologie oft auch vereinfachend als Isohypsen bezeichnet.
Isopykne	Linien gleicher Dichte z. B. Luftdichte, Wasserdichte.
Isoquante	Linien gleichen Outputs.
Isorrhachie	Linien zeitgleichen Hochwassereintritts.
Isoseiste	Linien gleicher (standortabhängiger) Intensität eines Erdbebens.
Isostere	Linien gleichen Bedeckungsgrads des Adsorbenten einer Adsorptionskältemaschine.
Isotache	Linien gleicher Geschwindigkeit (in der Regel Wind- oder Fließgeschwindigkeit).
Isothere	Linien gleicher durchschnittlicher Sommertemperatur.
Isotherme	Linien gleicher Temperatur.
Isothermomene	Linien gleicher Anzahl thermischer Vegetationszeiten in Monaten (Bezug: Klimatologie).
Isotime	Linien gleicher Transportkosten einzelner Produkte im Weberschen Industriestandortmodell.
Isovapore	Linien gleichen Sättigungsdampfdruckes.
Nullkline	Nullwachstums-Isolinien in gewöhnlichen Differentialgleichung, siehe Phasenraum.

Weblinks

Struktur und Wesen von Isolinienkarten. (Memento vom 30. September 2007 im Internet Archive) geoWEB Magazin – Institut für Geographie und Raumforschung, Graz

Einzelnachweise

quickdict.de

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] quickdict.de