Seismologie

Die Seismologie (altgriechisch σεισμός seismós „(Erd-)Erschütterung, Erdbeben“ und -logie) ist die Lehre von Erdbeben und der Ausbreitung seismischer Wellen in Festkörpern. Als Teilgebiet der Geophysik ist sie die wichtigste Methode, um den inneren Aufbau der Erde zu erforschen. Das eng verwandte Fachgebiet der Seismik erforscht hingegen das Erdinnere mittels künstlich angeregter seismischer Wellen und zählt zur Angewandten Geophysik. Die Messinstrumente für beide Forschungsbereiche befinden sich in den weltweit über 300 seismologischen Messstationen.

Aufgaben

Die Seismologie schickt sich an, das Erdinnere tomografisch in drei Dimensionen abzubilden. Heiße und kalte Massenströme werden durch die Anomalie der Geschwindigkeit seismischer Wellen sichtbar gemacht. Bei weiterer Verbesserung der Auflösung wird es möglich werden, die Materialströme im Erdmantel darzustellen, die erstens Antrieb für die Plattentektonik und zweitens Teil des Geodynamos sind, der das Erdmagnetfeld erzeugt.

Mit Hilfe von Seismographen (auch genannt Seismometer) werden seismische Wellen, die entweder die Erde durchlaufen oder sich entlang der Oberfläche ausbreiten, aufgezeichnet. Aus den Laufzeiten und Amplituden dieser Wellen lassen sich Rückschlüsse auf den inneren Aufbau der Erde ziehen. Die seismischen Eigenschaften eines Gebietes werden durch die Seismizität beschrieben. Durch Diagramme (Beach Balls) wird die räumliche Lage von Erdbebenherden dargestellt.

Im Gegensatz hierzu nutzt die Seismik aktive Quellen wie zum Beispiel Explosionen, um den Aufbau der Erdkruste und des oberen Erdmantels zu erkunden.

Ein verwandtes Forschungsgebiet ist die Erdspektroskopie, die sich mit vergleichsweise langwelligen seismischen Schwingungen befasst und deren Frequenzspektrum untersucht.

Geschichte

Als einer der Väter der Seismologie gilt Ernst von Rebeur-Paschwitz, dem 1889 die erste, noch zufällige Aufzeichnung eines Erdbebens gelang und der seine daraus folgenden Erkenntnisse veröffentlichte. Als eigene Wissenschaft wurde die Seismologie durch den deutschen Wissenschaftler Emil Wiechert (Begründer der Erdbebenwarte in Göttingen) eingeführt, der im Jahre 1899 den ersten Horizontalseismographen erfand. Weitere wichtige Personen in der Seismologie waren die Dänin Inge Lehmann, der Amerikaner Charles Francis Richter, der Deutschamerikaner Beno Gutenberg, der Engländer Harold Jeffreys, der Neuseeländer Keith Edward Bullen sowie Eric R. Engdahl und Edward A. Flinn, die ein Regionalisierungschema für Erdbebenregionen (Flinn-Engdahl-Regionen) erarbeiteten.

Bezüglich der Einführung erster Anwendungen in der Erdölprospektion hat sich ein Schüler Wiecherts, Ludger Mintrop, hervorgetan.

Moderne Verfahren in der Seismologie sind unter anderem die seismische Tomographie, die Receiver-Functions-Analyse, die Untersuchung von Vorläuferphasen oder Wellenfelduntersuchungen.

Seismogramme

Ein zentraler Punkt der Seismologie ist die Auswertung von Seismogrammen. Seismogramme zeichnen die Bewegung (Physik) relativ zum ruhenden Erdboden auf. Dabei wird zwischen verschiedenen Arten von Beben unterschieden. Man unterscheidet zwischen Fern-, Regional-, Lokal- und Mikrobeben und kann daran auch die maximale Entfernung des Erdbeben beurteilen.

Fernbeben werden unterhalb von 1 Hz aufgezeichnet. Diese Beben werden auf globalen Netzwerken aufgezeichnet und sie weisen ein gutes Signal-Rausch-Verhältnis auf. Regional- und Lokalbeben müssen in kleinskaligeren Netzen aufgezeichnet werden. Diese weisen wenige 10 bis 1000 km Abstand zum Epizentrum auf. Bei diesen Beben wird bereits höherfrequente Energie bis 100 Hz aufgezeichnet. Mikrobeben können nur von seismischen Stationen in unmittelbarer Nähe, im Bereich von wenigen Metern zum Epizentrum aufgezeichnet werden. Die Abtastrate beträgt minimal 1 kHz.

Seismogramme werden oft in drei Komponenten aufgezeichnet. Die Komponenten stehen orthogonal zueinander und werden in Counts aufgezeichnet. Diese sind im Durchlassbereich proportional zur Schwinggeschwindigkeit des Bodens.

Restitution

Die Umrechnung der Counts außerhalb des Durchlassbereiches in Bodenverschiebung wird Restitution genannt. Dies erhöht das Signal-Rausch-Verhältnis und verbessert die Möglichkeiten, die Phasen und Ankunftszeiten der Wellen zu identifizieren. Vor allem zur Magnitudenbestimmung sind restituierte Daten wichtig.

Rotation

Das Koordinatensystem eines Seismogramms kann in Richtung des Großkreises zwischen dem Erdbeben und dem Seismometer rotiert werden. Dies ist eine Koordinatentransformation aus den Horizontalkomponenten in Transversal- und Radialkomponenten. Man verwendet dazu die Epizentraldistanz, den Abstand des Seismometers von dem Erdbeben und den Azimuth, den Winkel am Seismometer der Epizentralstrecke zur Nordrichtung gemessen. Außerdem verwendet man den Backazimuth, der den Winkel zwischen den der Epizentralstrecke und der Nordrichtung am Epizentrum misst. Entgegen mathematischer Konventionen wird der Winkel im Uhrzeigersinn gemessen.

Seismische Strahlen

Seismische Strahlen sind eine hochfrequente Lösung der Bewegungsgleichung einer elastischen Erde. Sie bezeichnen die Trajektorie des Energietransportes in der Erde. Die Ausbreitungsrichtung des Strahls geschieht in Richtung des Langsamkeitsvektors oder alternativ des Wellenzahlvektors. Der Strahlwinkel wird zwischen der Vertikalen und dem Langsamkeitsvektor gemessen. Wendet man das Snelliussche Brechungsgesetz an, kann man nach $p={\frac {r\cdot \sin \varphi }{c}}$ einen konstanten Strahlparameter p ableiten, wobei $\varphi$ der Strahlwinkel, r der Erdradius und c die Ausbreitungsgeschwindigkeit der Welle sind.

Im rechten Winkel zu den seismischen Strahlen liegt die Wellenfront. Die Ebene der Wellenfront wird durch eine konstante Phase definiert. Diese Phasen der Wellenfronten werden an einer seismischen Station gemessen.

Konzept des Strahlenbündels

Der Energiefluss in einem Strahlenbündel ist bei variierendem Querschnitt des Bündels konstant. Dies ermöglicht die Abschätzung von Amplituden der seismischen Strahlen. Für das Konzept des Strahlenbündels macht man die Annahmen, dass keine Diffraktionen auftreten und die Wellen sich hochfrequent ausbreiten. Aus diesem Konzept folgt, dass ein Strahlenbündel mit großem Querschnitt kleine Amplituden und ein Strahlenbündel mit kleinem Querschnitt große Amplituden aufweist.

Laufzeitkurve

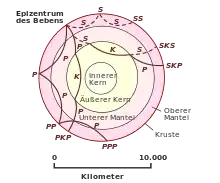
Seismische Strahlen verschiedener Phasen im Erdinneren

Globale Phasen	Nomenklatur
P-Welle durch Kruste und Mantel	P
P-Welle durch äußeren Kern	K
P-Welle durch inneren Kern	I
S-Welle durch Kruste und Mantel	S
S-Welle durch inneren Kern	J
Tertiäre Welle (teilweise Propagation durch Ozean)	T

Oberflächenwelle	Nomenklatur
Langperiodischen Oberflächenwelle (unbestimmt)	L
Rayleighwelle	R
Lovewelle	Q
Langperiodische Mantel-Love-Welle	G
Langperiodische Rayleighwelle (i. d. R. Airy-Phase)	LR
Langperiodische Lovewelle (i. d. R. Airy-Phase)	LQ

Raumwellenphase	Nomenklatur
P-Welle Scheitelpunkt in oberer Kruste (granitisch)	g
P-Welle Scheitelpunkt in oberer Kruste (basaltisch)	b
Refraktion im oberen Mantel	n
Außenreflexion an der Moho	m
Außenreflexion äußerer Kern	c
Außenreflexion innerer Kern	i
Reflexion an einer Diskontinuität	z
Diffraktierte Welle	diff

Unter Kenntnis der Zeit, wann das Erdbeben aufgetreten ist, kann man die Laufzeit der seismischen Strahlen errechnen. Aus den ermittelten Laufzeiten der seismischen Strahlen lassen sich nach dem Fermatschen Prinzip Laufzeitkurven bestimmen. Dazu wird die Laufzeit gegen die Epizentraldistanz aufgetragen.

Benndorf-Beziehung

Der Strahlparameter ist konstant für Strahlen mit gleichem Abstrahlwinkel. Für die Benndorf-Beziehung betrachten wir zwei parallel an der Oberfläche einfallende Strahlen.

{\frac {{\text{d}}\tau }{{\text{d}}x}}={\frac {r_{E}\cdot \sin \varphi }{c(z)}}=p

Es wird die Änderung der Laufzeit ${\text{d}}\tau$ gegen die Änderung der Epizentraldistanz ${\text{d}}x$ aufgetragen. Es folgt die Beziehung zwischen dem Strahlparameter p, der Ausbreitungsgeschwindigkeit c und dem Strahlwinkel $\varphi$ . Da sich der Term der Änderungen nur in horizontaler Ausbreitungsgeschwindigkeit ändert, können wir $\varphi =90^{\circ }$ setzen.

{\frac {{\text{d}}\tau }{{\text{d}}x}}={\frac {1}{c_{\mathrm {hor} }}}=s_{\mathrm {hor} }={\frac {p}{r_{E}}}

,

wobei ${\frac {1}{c_{\mathrm {hor} }}}$ die scheinbare horizontale Ausbreitungsgeschwindigkeit und $s_{\mathrm {hor} }$ die Horizontalkomponente des Langsamkeitsvektors ist. Daraus folgt für die Benndorf-Beziehung, dass die Tangente an einer Laufzeitkurve, aufgetragen gegen die Epizentraldistanz, dem Strahlparameter normiert auf den Erdradius entspricht. Daraus folgt, dass der Strahlparameter im Epizentrum seinen höchsten Wert annimmt und kontinuierlich mit der Entfernung abnimmt. In einer Epizentralentfernung von 180° fällt der Strahl senkrecht zur Oberfläche ein, und der Strahlparameter wird Null. Die horizontale Scheingeschwindigkeit steigt ins Unendliche an. Abweichende Beobachtungen werden für seismische Strahlen durch den Kern in einer Epizentralentfernung über 90° und bei Strahlen mit dem Apex in der Übergangszone zwischen Kruste und Mantel gemacht.

Strahlphasen

Die seismischen Strahlen werden nach ihrem Strahlverlauf bezeichnet. Die Nomenklatur dieser Phasen ist in den Tabellen rechts aufgeschlüsselt. Es können auch komplexe Phasen, wie Mehrfachreflexionen oder Wellenkonversionen benannt werden. Eine Reflexion einer P-Welle an der freien Oberfläche wird als PP bezeichnet. Bei entsprechenden Mehrfachreflexionen wird die Anzahl der Reflexionen der Phase vorangestellt. Eine 4-fach reflektierte S-Welle würde somit als 4S bezeichnet. Es können auch Phasen deklariert werden, dass Erdbebenherd in großer Tiefe liegt und in Richtung der Oberfläche abstrahlt. Dies wird als Tiefenphase bezeichnet und für P-Wellen als pP bezeichnet. Bei starken Erdbeben können die seismischen Strahlen genug Energie aufbringen um durch den Kern zu laufen und an der gegenüberliegenden Oberfläche der Erde gemessen zu werden, diese würde als PKIKP bezeichnet. Ein seismischer Strahl durch den inneren Kern kann eine Konversion in eine S-Welle erfahren und am Übergang zum äußeren Kern wieder in eine P-Welle konvertiert werden. Diese PKJKP-Phase konnte bisher nicht eindeutig identifiziert werden, da die P-S-Transmissions koeffizienten sehr kleine Amplituden aufweisen.

Theoretische Laufzeitkurven

Im Erdinneren gibt es Zonen mit starken Kontrasten der seismischen Ausbreitungsgeschwindigkeiten.

Starke Geschwindigkeitszunahme

An der Kruste-Mantel-Grenze steigt die Ausbreitungsgeschwindigkeit stark an. Das Laufzeitdiagramm einer solchen Zone zeigt zwei konkave Äste, die durch einen konvexen rücklaufenden Ast verbunden werden. Die zwei Spitzen an denen die drei Äste jeweils werden durch die seismischen Strahlen am Rand der Übergangszone definiert. Diese Spitzen werden kritische Punkte oder cusps genannt, sie setzen die Laufzeitkurve stetig fort. Zwischen den kritischen Punkten ist die Laufzeitkurve mehrdeutig. Der Strahlparameter in Abhängigkeit von der Epizentraldistanz ist eine stetig monoton fallende Funktion, auch sie ist zwischen den kritischen Punkten mehrdeutig. Die Umkehrfunktion hingegen lässt sich eindeutig bestimmen.

Geschwindigkeitsinversion

In der Übergangszone von Mantel zu Kern nimmt die Geschwindigkeit mit der Tiefe ab. Diese Inversionszone bildet eine Zone aus, an der keine seismischen Strahlen an die Oberfläche gelangen. Die Schattenzone wird von der Zone in der Tiefe generiert, in der keine Strahlenscheitel liegen.

Array-Seismologie

Array-Seismologie verbessert das Signal-Rausch Verhältnis und ermöglicht die direkte Messung der horizontalen Langsamkeit. Zudem ermöglicht sie es, Phaseneinsätze zu bestimmen und zu unterscheiden, sowie die Herdtiefe zu bestimmen.

Seismisches Array

Ein seismisches Array ist die räumliche Anordnung von Seismometern mit identischer Charakteristik und zentraler Datenerfassung. Dies können Geophonketten, Refraktionsauslagen oder seismische Netze sein. Teleseismische Beben können am besten ausgewertet werden, da die Wellenfronten ihr Signal über die Auslage kaum ändern und somit eine hohe Kohärenz aufweisen.

Richtstrahlbildung (Beamforming)

Bei der Richtstrahlbildung wird eine beliebige Station beobachtet und alle eintreffenden Signale werden anhand der horizontalen Langsamkeit auf die Ankunftszeit der entsprechenden Station normiert. Diese Signale können nun gestapelt werden. Dies verbessert die Signal-Noise Ratio, da die stochastisch auftretenden Störsignale destruktiv überlagert werden. Zudem wirkt diese Bearbeitung der Daten als Wellenzahlfilter. Dazu berechnet man die Energieaufnahme des auf die Langsamkeit abgestimmten Richtstrahls. Aus dieser Berechnung entsteht ein Gewichtungsfaktor, der als Arrayantwortfunktion bezeichnet wird:

\left|{\frac {1}{N}}\sum \limits _{m=0}^{N-1}e^{i\left({\vec {k}}-{\vec {k}}_{0}\right){\vec {r}}_{m}}\right|^{2}

,

wobei N die Anzahl der seismischen Stationen, k die Wellenzahl und r der Abstand ist. Im Idealfall wird die Arrayantwortfunktion der Dirac'schen Deltafunktion angenähert, dies schwächt Signale mit abweichender Langsamkeit ideal ab. Diese Methode ist verwandt mit der Common Midpoint-Methode in der angewandten Seismik.

Vespagramm

Um später eintreffende Phasen zu lokalisieren, können Vespagramme erstellt werden. Hierzu werden die schwächeren Phasen aus der Coda der stärkeren Phasen hervorgehoben. Da beide Phasen derselben Quelle entstammen unterscheiden sie sich nur in der Langsamkeit. Man unterteilt das Seismogramm in mehrere Zeitintervalle und bestimmt für jedes Intervall die Richtstrahlen mit variierendem Betrag der Langsamkeit. Anschließend wird die Langsamkeit gegen die Zeit aufgetragen.

Geschwindigkeitsinversion

Die Laufzeit kann aus einem gegebenen Geschwindigkeitsmodell des Untergrundes einfach bestimmt werden. Das inverse Problem ist, das Geschwindigkeitsmodell aus den gemessenen Laufzeiten zu ermitteln. Für eine Erde, in der die Geschwindigkeit mit der Tiefe zunimmt, lässt sich dieses Problem analytisch mit der Herglotz-Wiechert-Gleichung lösen. Wenn das Geschwindigkeitsmodell komplexer ist, wird ein numerisch iterativer, linearisierter Ansatz herangezogen. Dies wird als Geschwindigkeitstomographie oder Simultaninversion bezeichnet. Der Ansatz der Geschwindigkeitstomographie ist allerdings oft schlecht gestellt, mehrdeutig und hat eine schlechte Auflösung. Zudem konvergiert es langsam; einige Modelle sind ähnlich gute Abbildungen des Geschwindigkeitmodells. Diese Gründe machen ein gutes Startmodell des Untergrunds unersetzbar.

Herglotz-Wiechert-Verfahren

Das Herglotz-Wiechert-Verfahren wird angewandt, um ein 1D-Geschwindigkeitsmodell aus gemessenen Laufzeitkurven zu erstellen. Eine grundlegende Voraussetzung für dieses Verfahren ist, dass die Geschwindigkeit mit steigender Tiefe monoton zunimmt. Das bedeutet, dass im Untergrund keine Inversionszonen oder Niedergeschwindigkeitszonen auftreten dürfen. Diese Zonen können jedoch identifiziert und ausgeschlossen werden. Aus der Formel für die Epizentraldistanz, einem Variablenwechsel und partieller Integration ergibt sich die folgende Formel:

\pi \ln {\frac {R}{r_{1}}}=\int \limits _{\Delta =0}^{\Delta _{1}}\cosh ^{-1}\left({\frac {p(\Delta )}{\eta _{1}}}\right){\text{d}}\Delta

und $p(\Delta _{1})=\eta _{1}$ , wobei $\Delta$ die Epizentraldistanz, $p(\Delta )$ der Strahlparameter in Abhängigkeit von der Epizentraldistanz und $\eta _{1}={\frac {r_{1}}{c(r_{1})}}$ der Radius normiert auf die Ausbreitungsgeschwindigkeit sind. Dieser analytische Ansatz löst das inverse Problem eindeutig. Allerdings können einige Schwierigkeiten nicht gelöst werden:

Die Beziehung zwischen der Laufzeit bzw. dem Strahlparameter und der Ausbreitungsgeschwindigkeit ist nichtlinear. Kleine Änderungen in der Ausbreitungsgeschwindigkeit führen also zu unproportionalen Änderungen der Laufzeit bzw. des Strahlparameters.
Triplikationen in Laufzeiten, besonders späte Ankunftszeiten, sind schwer zu messen, aber nötig, um eine eindeutige Geschwindigkeitstiefenfunktion abzuleiten.
Niedergeschwindigkeitszonen können nicht aufgelöst werden.
Da stetige Funktionen für die Laufzeit und den Strahlparameter benötigt werden, muss interpoliert werden. Diese Ergebnisse variieren jedoch mit dem Interpolationsverfahren.

Lokalisierung

Die Lokalisierung von Erdbeben dient der Bestimmung des Erdbebenherdes. Es wird dabei das Hypozentrum, das Epizentrum, was die Projektion des Hypozentrums an der Erdoberfläche darstellt, und das seismische Moment ermittelt.

Geigermethode

Die Geigermethode ist eine iterative Gradientenmethode zur Lokalisierung von Erdbebenherden. Dafür verwendet man aus Seismogrammen bestimmte Ankunftszeiten. Dabei wird davon ausgegangen, dass mehr als vier Ankunftszeiten an mehr als zwei Stationen gemessen werden können. Für gewöhnlich werden mehrere Stationen betrachtet. Außerdem wird vorausgesetzt, dass das Geschwindigkeitsmodell des Untergrundes bekannt ist. Die Ankunftszeit der Phasen der Erdbebenwellen ist somit eine nichtlineare Funktion von vier Unbekannten, der Herdzeit und der drei Koordinaten. Für die Geigermethode mit grober Kenntnis der Herdparameter wurde das Inversionproblem linearisiert:

\delta t=G\Delta m

,

wobei $\delta t$ die Ankunftszeit-Residuen, G die Jacobi-Matrix und $\Delta m$ der unbekannte Modellvektor sind. Dieses Gleichungssystem ist in der Regel überbestimmt und kann durch Minimalisierung der Fehlerquadrate gelöst werden. Die somit verbesserten Herdparameter können korrigiert und durch erneute Anwendung dieses Verfahrens weiter verbessert werden. In den Matrizen können lineare Abhängigkeiten entstehen, wodurch sich Parameter nicht unabhängig voneinander bestimmen lassen.

Die Tiefe des Erdbebenherdes lässt sich gut durch PKP- oder PKiKP-Phasen auflösen, wohingegen Pn- als auch Sn-Phasen gänzlich ungeeignet dafür sind. Die PKP- sowie die PKiKP-Phasen sind in Seismogrammen allerdings schwer zu erkennen. Das Epizentrum eines Bebens lässt sich am besten auflösen, wenn die Epizentraldistanz zwischen 2 und 5 Grad liegt. Aus geometrischen Betrachtungen folgt, dass der Abstrahlwinkel circa 90 Grad beträgt. Die gleichzeitige Benutzung von P- und S-Ankunftszeiten erhöht die Auflösbarkeit des Hypozentrums enorm, da durch die Abhängigkeit der seismischen Geschwindigkeit $c_{P}\approx {\sqrt {3}}c_{S}$ , Proportionalitäten in der Jacobi-matrix aufgehoben. Der Ablesefehler für S-Phasen ist jedoch wesentlich höher.

Stationskorrekturen

Das Geschwindigkeitsmodell des Untergrundes birgt besonders im Oberflächenbereich Probleme, da dort durch Verwitterung und Sedimentablagerungen starke Heterogenitäten auftreten. Die Abweichungen können Fehler in der Lokalisierung um bis zu 10 km verursachen. An diesen Stationen werden mittlere Laufzeitresiduen aus einem großen Satz an lokalisieren Erdbeben bestimmt. Es wird angenommen, dass Phasen immer den gleichen Laufzeitfehler haben.

Literatur

Monika Gisler: Göttliche Natur?: Formationen im Erdbebendiskurs der Schweiz des 18. Jahrhunderts. Dissertation. Chronos, Zürich 2007, ISBN 978-3-0340-0858-7.
Friedemann Wenzel (Hrsg.): Perspectives in modern seismology. (= Lecture notes in earth sciences. Vol. 105). Springer, Berlin 2005, ISBN 3-540-23712-7. (englisch)
Jan T. Kozák, Rudolf Dušek: Seismologische Karten – Ein Beispiel thematischer Kartographie. In: Cartographica Helvetica. Heft 27, 2003, S. 27–35. (Volltext)
Hugh Doyle: Seismology. Wiley, Chichester 1995, ISBN 0-471-94869-1. (englisch)
Thorsten Dahm: Vorlesungsskript: Seismologie I Laufzeiten, Lokalisierung, Tomographie. Hamburg 2010.
E. Wiechert, K. Zoeppritz: Ueber Erdbebenwellen. 1907.
E. Wiechert, L. Geiger: Bestimmung des Weges der Erdbebenwellen im Erdinnern. In: Physikalische Zeitschrift. 11, 1910, S. 294–311.
A. A. Fitch: Seismic reflection interpretation. Borntraeger, Berlin 1976, S. 139–142.
S. Rost, C. Thomas: Array seismology: Methods and applications. In: Reviews of Geophysics. 40(3), 2002, S. 1008. doi:10.1029/2000RG000100
Peter M. Shearer: Introduction to Seismology. 2., korr. Auflage. Cambridge University Press, 2011, ISBN 978-0-521-70842-5

Weblinks

Commons: Seismology – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Seismologie – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Podcast Interview mit Prof. Heiner Igel zu den Grundlagen der Seismologie abgerufen am 15. Juli 2010
Online-Lexikon zum Herglotz-Wiechert-Verfahren

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.