Isophote

Eine Isophote ist in der Geometrie eine Kurve auf einer beleuchteten Fläche, die Punkte gleicher Helligkeit verbindet. Dabei wird vorausgesetzt, dass die Fläche mit parallelem Licht beleuchtet wird und die Helligkeit $h$ in einem Flächenpunkt $P$ mit dem folgenden Skalarprodukt gemessen wird:

h(P)={\vec {n}}(P)\cdot {\vec {v}}=\cos \varphi \ .

Ellipsoid mit Isophoten (rot)

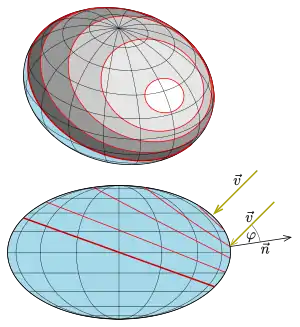
Dabei ist ${\vec {n}}(P)$ der Einheitsnormalenvektor im Flächenpunkt $P$ und ${\vec {v}}$ der Einheitslichtvektor. Ist $h(P)=0$ , d. h. die Lichtrichtung senkrecht zur Normale, so ist $P$ ein Punkt des Flächenumrisses bei Parallelprojektion in Richtung ${\vec {v}}$ . Helligkeit 1 bedeutet, das Licht fällt in dem Punkt P senkrecht auf die Fläche. Eine Ebene besitzt keine Isophoten, da jeder Punkt der Ebene die gleiche Helligkeit besitzt.

In der Astronomie versteht man unter einer Isophote eine Kurve auf einer Photographie, die Punkte gleicher Helligkeit verbindet.[1]

Anwendung mit Beispiel

Isophoten werden im CAD-Bereich als Testkurven verwendet, um die Güte von Flächenübergängen optisch zu beurteilen. Denn bei einer genügend differenzierbaren Fläche (implizit oder parametrisiert) hängt der Normalenvektor der Fläche von den ersten Ableitungen ab. Die Differenzierbarkeit der Isophoten und damit ihre geometrische Stetigkeit ist also gegenüber der Fläche um 1 reduziert. Sind in einem Punkt der Fläche nur die Tangentialebenen stetig (d. h. $G^{1}$ -stetig), so besitzt die Isophote in diesem Punkt einen Knick (d. h. ist nur $G^{0}$ -stetig).

In dem folgenden Beispiel (s. Bild) werden zwei sich schneidende Tensorprodukt-Bezierflächen mit Hilfe einer Übergangsfläche ausgerundet. Links hat die Übergangsfläche nur $G^{1}$ -kontakt mit den Bezierflächen, rechts $G^{2}$ -Kontakt. Dieser Unterschied ist ohne die Isophoten nicht zu erkennen. Erst die Isophoten zeigen den Unterschied: links haben die Isophoten Knicke, rechts sind sie glatt.

Isophoten auf zwei Bezierflächen und einer dazu G1- bzw. G2-stetige Übergangsfläche:links G1-stetig, rechts G2-stetig, d. h. die Isophoten sind links nur G0-stetig (haben einen Knick), rechts sind die Isophoten glatt

Bestimmung von Punkten einer Isophote

Für eine implizite Fläche

Ist die Fläche implizit durch eine Gleichung $f(x,y,z)=0$ gegeben, so lautet die Isophoten-Bedingung

{\frac {\nabla f\cdot {\vec {v}}}{|\nabla f|}}=c\ .

Um Punkte der zu einem vorgegebenen $c$ gehörigen Isophote zu bestimmen, muss man also Lösungen des nicht linearen Gleichungssystems

$\ f(x,y,z)=0,\qquad \nabla f(x,y,z)\cdot {\vec {v}}-c\;|\nabla f(x,y,z)|=0\$

bestimmen. Dieses System kann man als Schnitt zweier impliziter Flächen ansehen und mit dem Verfolgungsalgorithmus von Bajaj et al. (s. Literatur) genügend viele Punkte berechnen.

Für parametrisierte Flächen

Ist die Fläche parametrisiert durch ${\vec {x}}={\vec {S}}(s,t)$ gegeben, so lautet die Isophotenbedingung

{\frac {({\vec {S}}_{s}\times {\vec {S}}_{t})\cdot {\vec {v}}}{|{\vec {S}}_{s}\times {\vec {S}}_{t}|}}=c\ .

Diese Gleichung kann man in die Gleichung

$\ ({\vec {S}}_{s}\times {\vec {S}}_{t})\cdot {\vec {v}}-c\;|{\vec {S}}_{s}\times {\vec {S}}_{t}|=0$

umformen. Diese Gleichung beschreibt in der s-t-Ebene eine implizite Kurve, für die man mit einem Verfolgungsalgorithmus (s. implizite Kurve) genügend viele Punkte bestimmen und anschließend mit ${\vec {S}}(s,t)$ Flächenpunkte berechnen kann.

Siehe auch

Isolinie

Literatur

J. Hoschek, D. Lasser: Grundlagen der geometrischen Datenverarbeitung, Teubner-Verlag, Stuttgart, 1989, ISBN 3-519-02962-6, S. 31.
Z. Sun, S. Shan, H. Sang et al.: Biometric Recognition, Springer, 2014, ISBN 978-3-319-12483-4, S. 158.
C.L. Bajaj, C.M. Hoffmann, R.E. Lynch, J.E.H. Hopcroft: Tracing Surface Intersections, (1988) Comp. Aided Geom. Design 5, S. 285–307.

J. Binney, M. Merrifield: Galactic Astronomy, Princeton University Press, 1998, ISBN 0-691-00402-1, S. 178.

Weblinks

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] J. Binney, M. Merrifield: Galactic Astronomy, Princeton University Press, 1998, ISBN 0-691-00402-1, S. 178.